2022-2023学年苏科版 八年级数学下册 平行四边形-单元复习课件单元复习PPT(共31张PPT )
文档属性
| 名称 | 2022-2023学年苏科版 八年级数学下册 平行四边形-单元复习课件单元复习PPT(共31张PPT ) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 16:58:14 | ||
图片预览










文档简介
(共31张PPT)
第九章 中心对称图形—平行四边形
知
识
大
全
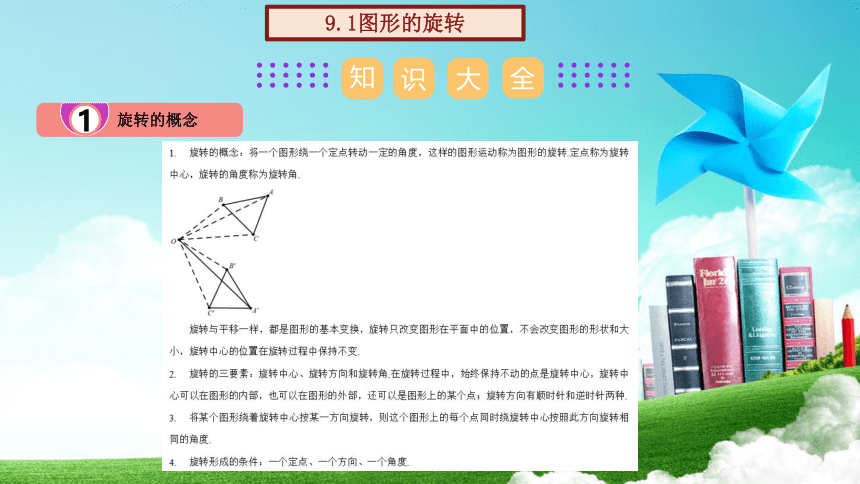
旋转的概念
1
9.1图形的旋转
知
识
大
全
典例
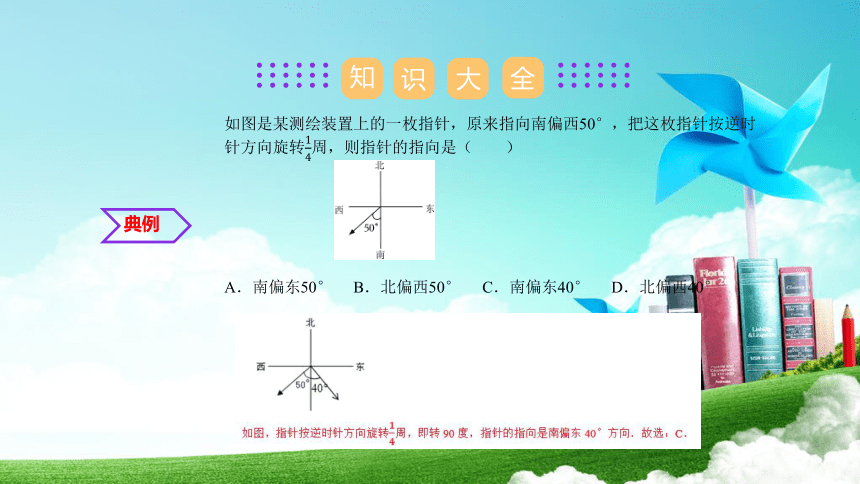
如图是某测绘装置上的一枚指针,原来指向南偏西50°,把这枚指针按逆时针方向旋转周,则指针的指向是( )
A.南偏东50° B.北偏西50° C.南偏东40° D.北偏西40°
知
识
大
全
旋转的性质
2
知
识
大
全
典例
如图,在△ABC中,AB=BC,∠ABC=α°,点D为AC边上一点,将BD绕点D顺时针旋转α°至ED,使E,B在AC异侧,连接CE,若∠BCE=β°,则α与β的关系是 .
知
识
大
全
旋转作图
3
知
识
大
全
典例
如图,已知△ABC的三个顶点坐标为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)请画出△ABC关于坐标原点O的中心对称图形△A′B′C′,并写出点A的对应点A′的坐标 ;
(2)请直接写出:以A、B、C、D为顶点的平行四边形的第四个顶点D的坐标 .
【解答】解:(1)如图,△A′B′C′即为所求,A′( 2,﹣3).
故答案为:(2,﹣3);
(2)如图,点D即为所求,D(﹣7,3)或(3,3)或(﹣5,﹣3).
故答案为:(﹣7,3)或(3,3)或(﹣5,﹣3).
知
识
大
全
中心对称
1
9.2 中心对称与中心对称图形
知
识
大
全
典例
下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
【解答】解:根据中心对称的概念,知②③④都是中心对称.
故选:C.
知
识
大
全
中心对称的性质
2
知
识
大
全
典例
若两个图形成中心对称,则下列说法:
①对应点的连线必经过对称中心;
②这两个图形的形状和大小完全相同;
③这两个图形的对应线段一定相等;
④将一个图形绕对称中心旋转某个角度后必与另一个图形重合.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:∵两个图形成中心对称,
∴①对应点的连线必经过对称中心,正确;
②这两个图形的形状和大小完全相同,正确;
③这两个图形的对应线段一定相等,正确;
④将一个图形绕对称中心旋转某个角度后必与另一个图形重合错误,必须旋转180°才能够重合.
综上所述,正确的由①②③共3个.
故选:C.
知
识
大
全
中心对称作图
3
典例
知
识
大
全
中心对称图形
4
知
识
大
全
典例
下列图案中,既是中心对称图形又是轴对称图形的是( )
【解答】解:A.该图形不是中心对称图形,是轴对称图形;故A不符合题意;
B.该图形是轴对称图形,不是中心对称图形;故B不符合题意;
C.该图形是轴对称图形,又是中心对称图形;故C符合题意;
D.该图形是轴对称图形,不是中心对称图形;故D不符合题意.
故选:C.
知
识
大
全
平行四边形定义
1
9.3 平行四边形
知
识
大
全
平行四边形的性质
2
知
识
大
全
典例
如图,在平行四边形ABCD中,∠A﹣∠B=50°,则∠A的度数是( )
A.130° B.115° C.65° D.50°
【解答】解:在平行四边形ABCD中,∠A+∠B=180°,
又有∠A﹣∠B=50°,
把这两个式子相加即可求出∠A=115°,
故选:B.
知
识
大
全
平行四边形的判定
3
知
识
大
全
典例
如图,已知在四边形BCDE中,CD∥BE,点F是DE的中点,连接CF交BE于点A,且点E是AB的中点,求证:四边形BCDE是平行四边形.
知
识
大
全
反证法
4
典例
知
识
大
全
矩形
1
9.3 矩形、菱形、正方形
知
识
大
全
矩形
1
知
识
大
全
典例
如图,菱形ABCD对角线交于点O,CE∥BD,BE∥AC.求证:四边形OBEC是矩形.
【解答】证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∵CE∥BD,BE∥AC,
∴四边形CEBO是平行四边形,
又∵AC⊥BD,
∴四边形OBEC是矩形.
知
识
大
全
菱形
2
知
识
大
全
典例
已知:如图,把菱形ABCD沿着AC方向平移得到菱形A1B1C1D1,BC与A1B1相交于点E,DC与A1D1相交于点F.求证:四边形A1ECF是菱形.
知
识
大
全
正方形
3
知
识
大
全
典例
如图,E、F、M、N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.求证:四边形EFMN是正方形.
【解答】解:四边形EFMN是正方形.
证明:∵AE=BF=CM=DN,
∴AN=DM=CF=BE.
∵∠A=∠B=∠C=∠D=90°,∴△AEN≌△DMN≌△CFM≌△BEF.
∴EF=EN=NM=MF,∠ENA=∠DMN.∴四边形EFMN是菱形.
∵∠ENA=∠DMN,∠DMN+∠DNM=90°,∴∠ENA+∠DNM=90°.
∴∠ENM=90°.∴四边形EFMN是正方形.
知
识
大
全
三角形的中位线的概念及定理
1
9.4 三角形的中位线
知
识
大
全
典例
知
识
大
全
中点四边形
2
知
识
大
全
典例
第九章 中心对称图形—平行四边形
知
识
大
全
旋转的概念
1
9.1图形的旋转
知
识
大
全
典例
如图是某测绘装置上的一枚指针,原来指向南偏西50°,把这枚指针按逆时针方向旋转周,则指针的指向是( )
A.南偏东50° B.北偏西50° C.南偏东40° D.北偏西40°
知
识
大
全
旋转的性质
2
知
识
大
全
典例
如图,在△ABC中,AB=BC,∠ABC=α°,点D为AC边上一点,将BD绕点D顺时针旋转α°至ED,使E,B在AC异侧,连接CE,若∠BCE=β°,则α与β的关系是 .
知
识
大
全
旋转作图
3
知
识
大
全
典例
如图,已知△ABC的三个顶点坐标为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)请画出△ABC关于坐标原点O的中心对称图形△A′B′C′,并写出点A的对应点A′的坐标 ;
(2)请直接写出:以A、B、C、D为顶点的平行四边形的第四个顶点D的坐标 .
【解答】解:(1)如图,△A′B′C′即为所求,A′( 2,﹣3).
故答案为:(2,﹣3);
(2)如图,点D即为所求,D(﹣7,3)或(3,3)或(﹣5,﹣3).
故答案为:(﹣7,3)或(3,3)或(﹣5,﹣3).
知
识
大
全
中心对称
1
9.2 中心对称与中心对称图形
知
识
大
全
典例
下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
【解答】解:根据中心对称的概念,知②③④都是中心对称.
故选:C.
知
识
大
全
中心对称的性质
2
知
识
大
全
典例
若两个图形成中心对称,则下列说法:
①对应点的连线必经过对称中心;
②这两个图形的形状和大小完全相同;
③这两个图形的对应线段一定相等;
④将一个图形绕对称中心旋转某个角度后必与另一个图形重合.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:∵两个图形成中心对称,
∴①对应点的连线必经过对称中心,正确;
②这两个图形的形状和大小完全相同,正确;
③这两个图形的对应线段一定相等,正确;
④将一个图形绕对称中心旋转某个角度后必与另一个图形重合错误,必须旋转180°才能够重合.
综上所述,正确的由①②③共3个.
故选:C.
知
识
大
全
中心对称作图
3
典例
知
识
大
全
中心对称图形
4
知
识
大
全
典例
下列图案中,既是中心对称图形又是轴对称图形的是( )
【解答】解:A.该图形不是中心对称图形,是轴对称图形;故A不符合题意;
B.该图形是轴对称图形,不是中心对称图形;故B不符合题意;
C.该图形是轴对称图形,又是中心对称图形;故C符合题意;
D.该图形是轴对称图形,不是中心对称图形;故D不符合题意.
故选:C.
知
识
大
全
平行四边形定义
1
9.3 平行四边形
知
识
大
全
平行四边形的性质
2
知
识
大
全
典例
如图,在平行四边形ABCD中,∠A﹣∠B=50°,则∠A的度数是( )
A.130° B.115° C.65° D.50°
【解答】解:在平行四边形ABCD中,∠A+∠B=180°,
又有∠A﹣∠B=50°,
把这两个式子相加即可求出∠A=115°,
故选:B.
知
识
大
全
平行四边形的判定
3
知
识
大
全
典例
如图,已知在四边形BCDE中,CD∥BE,点F是DE的中点,连接CF交BE于点A,且点E是AB的中点,求证:四边形BCDE是平行四边形.
知
识
大
全
反证法
4
典例
知
识
大
全
矩形
1
9.3 矩形、菱形、正方形
知
识
大
全
矩形
1
知
识
大
全
典例
如图,菱形ABCD对角线交于点O,CE∥BD,BE∥AC.求证:四边形OBEC是矩形.
【解答】证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∵CE∥BD,BE∥AC,
∴四边形CEBO是平行四边形,
又∵AC⊥BD,
∴四边形OBEC是矩形.
知
识
大
全
菱形
2
知
识
大
全
典例
已知:如图,把菱形ABCD沿着AC方向平移得到菱形A1B1C1D1,BC与A1B1相交于点E,DC与A1D1相交于点F.求证:四边形A1ECF是菱形.
知
识
大
全
正方形
3
知
识
大
全
典例
如图,E、F、M、N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.求证:四边形EFMN是正方形.
【解答】解:四边形EFMN是正方形.
证明:∵AE=BF=CM=DN,
∴AN=DM=CF=BE.
∵∠A=∠B=∠C=∠D=90°,∴△AEN≌△DMN≌△CFM≌△BEF.
∴EF=EN=NM=MF,∠ENA=∠DMN.∴四边形EFMN是菱形.
∵∠ENA=∠DMN,∠DMN+∠DNM=90°,∴∠ENA+∠DNM=90°.
∴∠ENM=90°.∴四边形EFMN是正方形.
知
识
大
全
三角形的中位线的概念及定理
1
9.4 三角形的中位线
知
识
大
全
典例
知
识
大
全
中点四边形
2
知
识
大
全
典例
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
