2022-2023学年北师大版数学八年级下册第一章 三角形的证明 单元训练(含答案)
文档属性
| 名称 | 2022-2023学年北师大版数学八年级下册第一章 三角形的证明 单元训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 883.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 17:00:51 | ||
图片预览

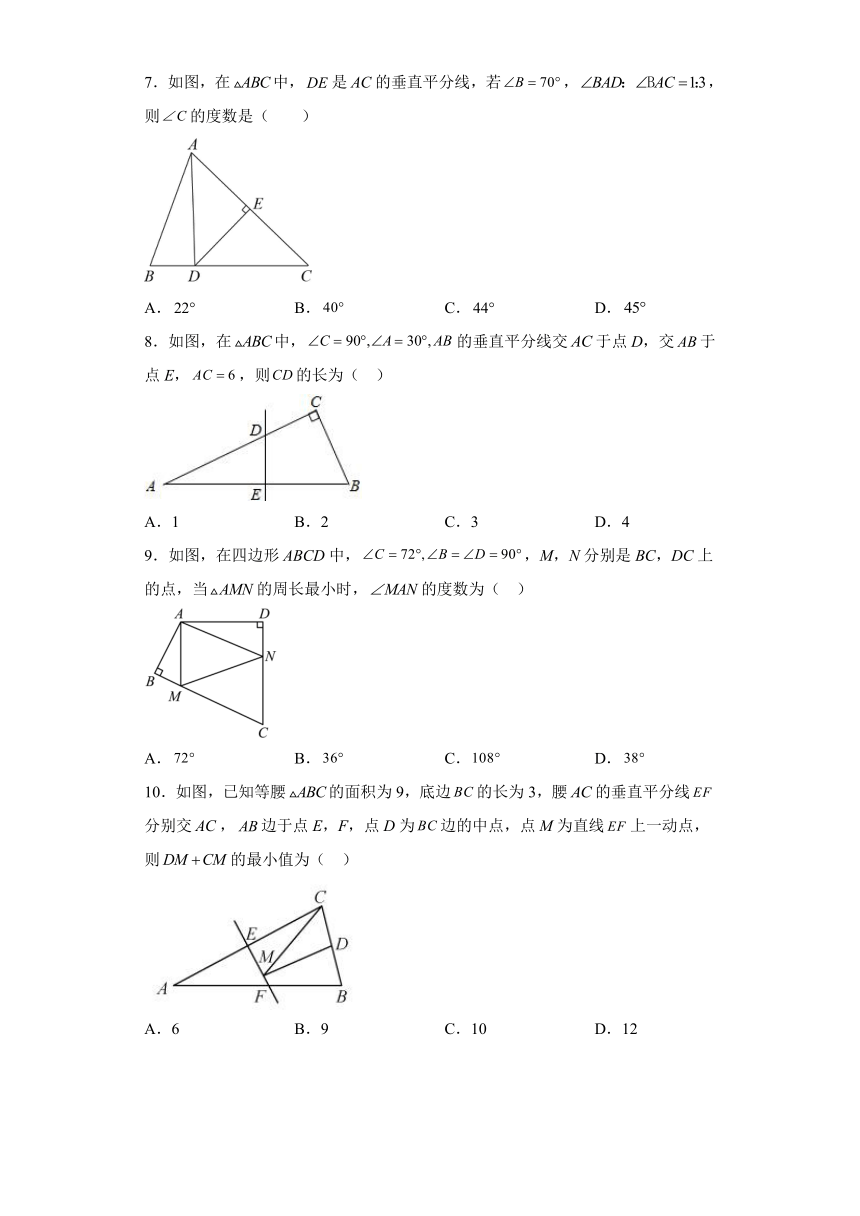
文档简介
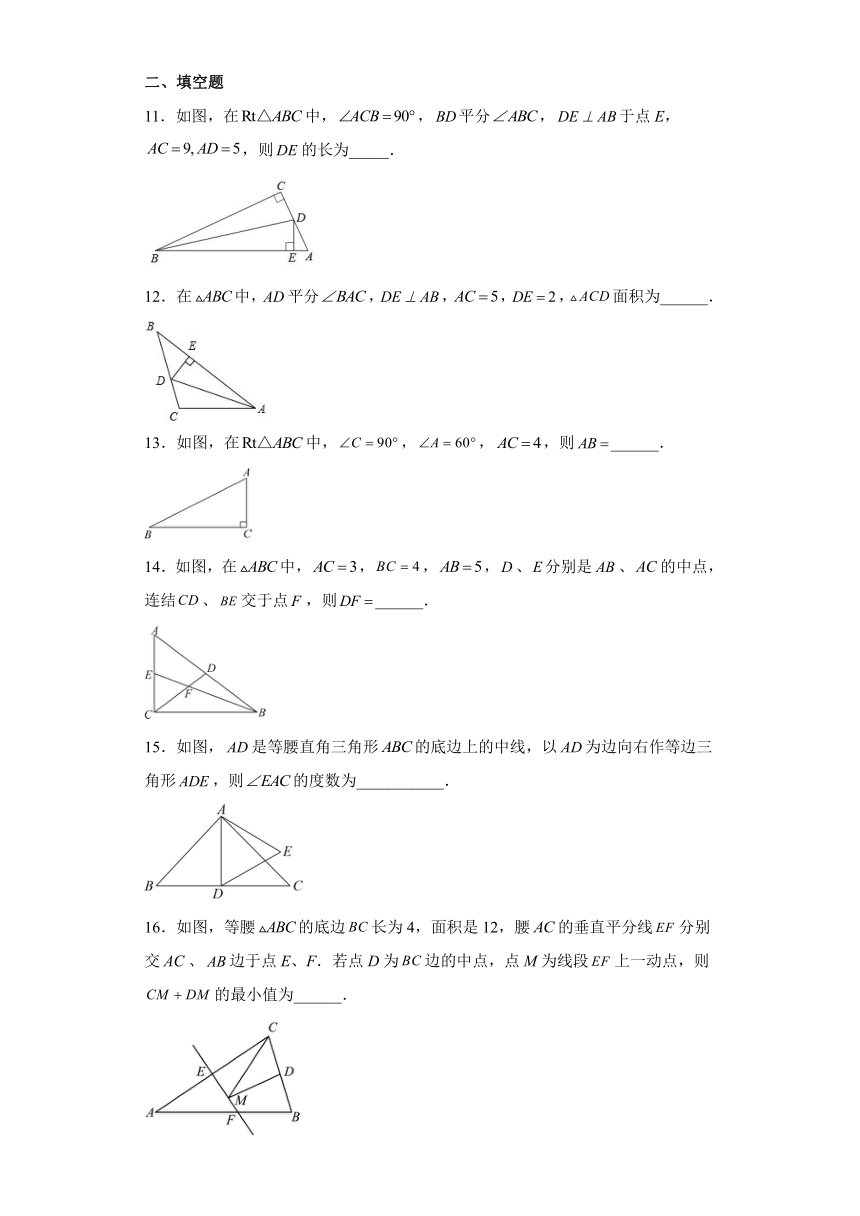
第一章 三角形的证明 单元训练
一、单选题
1.已知等腰三角形的一个角等于40°,则它的底角为( )
A. B. C.或 D.或
2.如图,已知.按照以下步骤作图:①以点为圆心,以适当的长为半径作弧,分别交的两边于,两点,连接.②分别以点,为圆心,以大于线段的长为半径作弧,两弧在内交于点,连接,.③连接交于点.下列结论中不正确的是( )
A. B.
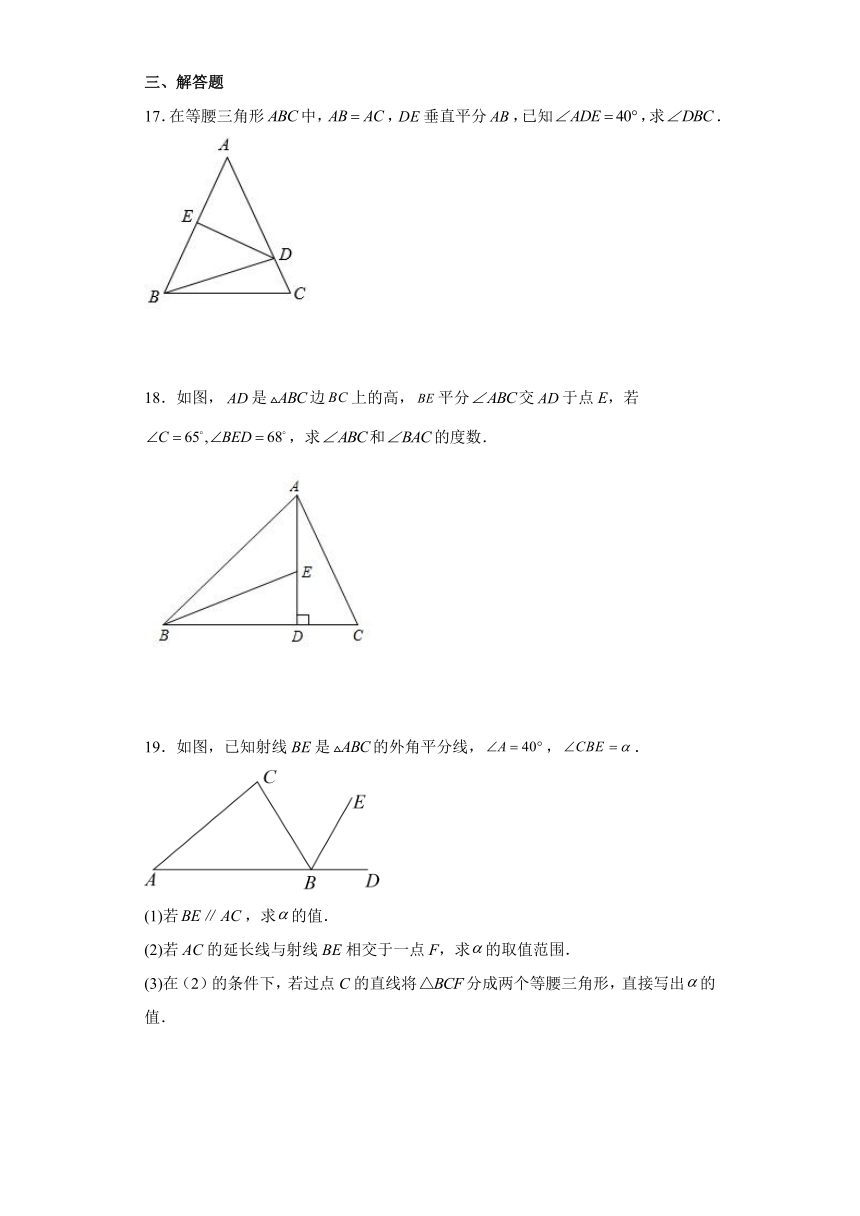
C. D.
3.在中,,,,的对边分别是a,b,c,下列条件中,不能判断为直角三角形的是( )
A.,,, B.
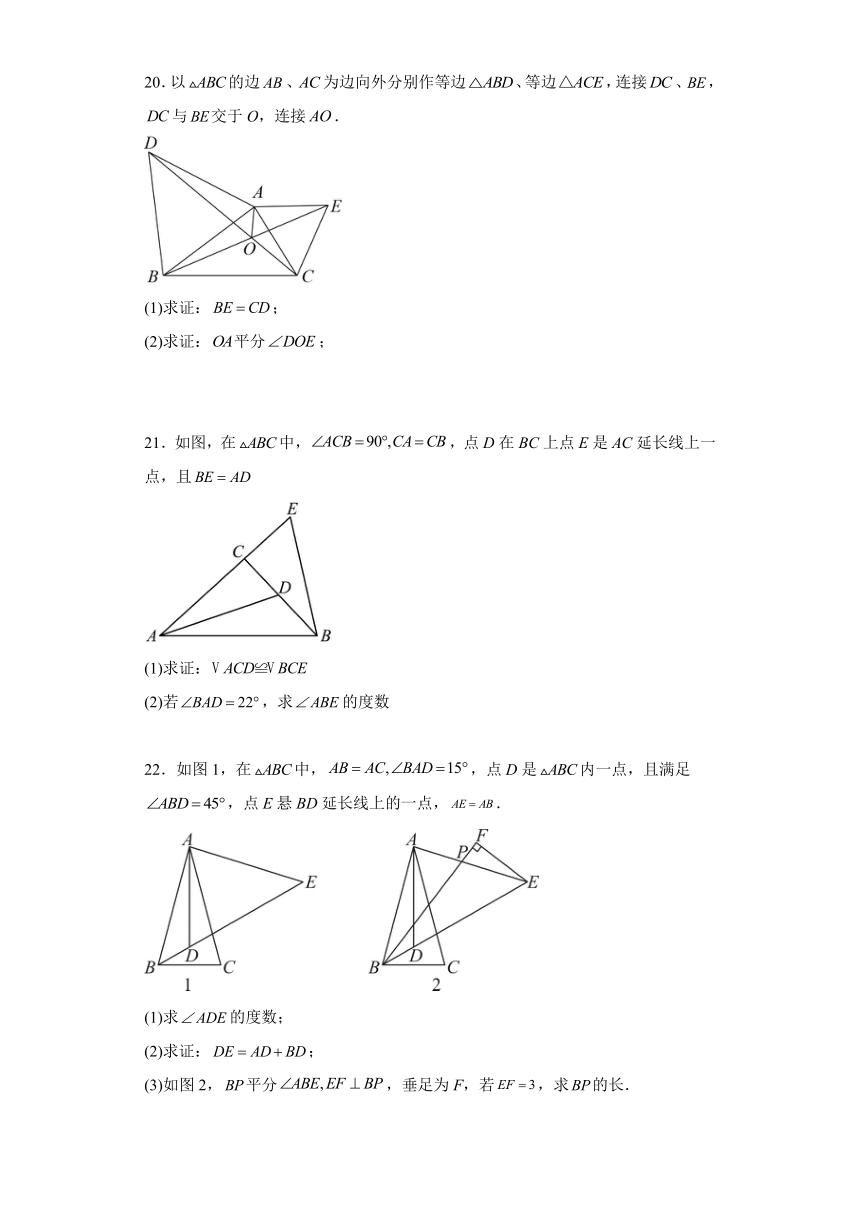
C. D.
4.若a,b为等腰的两边,且,则的周长为( )
A.12 B.9 C.12或9 D.12或15
5.如图,在中,,垂直平分,分别交,,于D,E两点,若,,则的长为( )
A.2 B.3 C.4 D.5
6.如图,在中,CD是AB边上的高,BE平分,交CD于点E,已知,,,则的面积等于( )
A.4 B.6 C.8 D.10
7.如图,在中,是的垂直平分线,若,,则的度数是( )
A. B. C. D.
8.如图,在中,的垂直平分线交于点D,交于点E,,则的长为( )
A.1 B.2 C.3 D.4
9.如图,在四边形ABCD中,,M,N分别是BC,DC上的点,当的周长最小时,的度数为( )
A. B. C. D.
10.如图,已知等腰的面积为9,底边的长为3,腰的垂直平分线分别交,边于点E,F,点D为边的中点,点M为直线上一动点,则的最小值为( )
A.6 B.9 C.10 D.12
二、填空题
11.如图,在中,,平分,于点E,,则的长为_____.
在中,平分,,,,面积为______.
13.如图,在中,,,,则______.
14.如图,在中,,,,、分别是、的中点,连结、交于点,则______.
15.如图,是等腰直角三角形的底边上的中线,以为边向右作等边三角形,则的度数为___________.
16.如图,等腰的底边长为4,面积是12,腰的垂直平分线分别交、边于点E、F.若点D为边的中点,点M为线段上一动点,则的最小值为______.
三、解答题
17.在等腰三角形中,,垂直平分,已知,求.
18.如图,是边上的高,平分交于点E,若,求和的度数.
19.如图,已知射线BE是的外角平分线,,.
(1)若,求的值.
(2)若AC的延长线与射线BE相交于一点F,求的取值范围.
(3)在(2)的条件下,若过点C的直线将分成两个等腰三角形,直接写出的值.
20.以的边、为边向外分别作等边、等边,连接、,与交于O,连接.
(1)求证:;
(2)求证:平分;
21.如图,在中,,点D在BC上点E是AC延长线上一点,且
(1)求证:
(2)若,求的度数
22.如图1,在中,,点D是内一点,且满足,点E悬BD延长线上的一点,.
(1)求的度数;
(2)求证:;
(3)如图2,平分,垂足为F,若,求的长.
参考答案:
一、选择1.D2.C3.D4.A5.C6.C7.C8.B9.B10.A
二、填空11.412.13.814.15.16.6
三、解答
17.∵垂直平分,
∴,,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
18.解:证明:
是边上的高
平分
19.(1)∵平分,
∴,
即:
(2)由AC的延长线与射线BE相交于一点F知与不平行,
∵是的外角,
∴,
∵平分,
∴
∵
∴
又
∴
∴
(3)设过点C的直线交于点G,此时,均为等腰三角形,
①当时,则有,,,
又,
②当时,,
,
,
,
③当时,
,
故此情况不存在,
④当,时,,,
,
,
又且
,
;
⑤当时,则,,
又,
∴
又
∴
解得,
故此情况不存在,
综上,的值为,或
20.(1)证明:∵ 和 都是等边三角形,
∴,,,
∴,即.
在△ABE 和△ADC 中
,
∴,
∴.
(2)证明:过点 A 分别作 ,,垂足为点 M,N.
∵由(1)知:,
∴
∴
∴
∴点 A 在的平分线上, 即 平分.
21.(1)∵
在与中
∴
(2)∵
∴
∵,
∴
∴
∴
∴
22.(1)解:∵,,
∴;
(2)如图1,在线段上截取,连接,
∵,,
∴是等边三角形,
∴
∵,
∴,
∴,
∴,
∵,
∴;
(3)延长交的延长线于点N,
由(2)及图1得,是等边三角形,
,
,
,
∴, 又,
∴,
∴,
∵既是的角平分线又是高,
,
∴是的中线,
即:,
.
一、单选题
1.已知等腰三角形的一个角等于40°,则它的底角为( )
A. B. C.或 D.或
2.如图,已知.按照以下步骤作图:①以点为圆心,以适当的长为半径作弧,分别交的两边于,两点,连接.②分别以点,为圆心,以大于线段的长为半径作弧,两弧在内交于点,连接,.③连接交于点.下列结论中不正确的是( )
A. B.
C. D.
3.在中,,,,的对边分别是a,b,c,下列条件中,不能判断为直角三角形的是( )
A.,,, B.
C. D.
4.若a,b为等腰的两边,且,则的周长为( )
A.12 B.9 C.12或9 D.12或15
5.如图,在中,,垂直平分,分别交,,于D,E两点,若,,则的长为( )
A.2 B.3 C.4 D.5
6.如图,在中,CD是AB边上的高,BE平分,交CD于点E,已知,,,则的面积等于( )
A.4 B.6 C.8 D.10
7.如图,在中,是的垂直平分线,若,,则的度数是( )
A. B. C. D.
8.如图,在中,的垂直平分线交于点D,交于点E,,则的长为( )
A.1 B.2 C.3 D.4
9.如图,在四边形ABCD中,,M,N分别是BC,DC上的点,当的周长最小时,的度数为( )
A. B. C. D.
10.如图,已知等腰的面积为9,底边的长为3,腰的垂直平分线分别交,边于点E,F,点D为边的中点,点M为直线上一动点,则的最小值为( )
A.6 B.9 C.10 D.12
二、填空题
11.如图,在中,,平分,于点E,,则的长为_____.
在中,平分,,,,面积为______.
13.如图,在中,,,,则______.
14.如图,在中,,,,、分别是、的中点,连结、交于点,则______.
15.如图,是等腰直角三角形的底边上的中线,以为边向右作等边三角形,则的度数为___________.
16.如图,等腰的底边长为4,面积是12,腰的垂直平分线分别交、边于点E、F.若点D为边的中点,点M为线段上一动点,则的最小值为______.
三、解答题
17.在等腰三角形中,,垂直平分,已知,求.
18.如图,是边上的高,平分交于点E,若,求和的度数.
19.如图,已知射线BE是的外角平分线,,.
(1)若,求的值.
(2)若AC的延长线与射线BE相交于一点F,求的取值范围.
(3)在(2)的条件下,若过点C的直线将分成两个等腰三角形,直接写出的值.
20.以的边、为边向外分别作等边、等边,连接、,与交于O,连接.
(1)求证:;
(2)求证:平分;
21.如图,在中,,点D在BC上点E是AC延长线上一点,且
(1)求证:
(2)若,求的度数
22.如图1,在中,,点D是内一点,且满足,点E悬BD延长线上的一点,.
(1)求的度数;
(2)求证:;
(3)如图2,平分,垂足为F,若,求的长.
参考答案:
一、选择1.D2.C3.D4.A5.C6.C7.C8.B9.B10.A
二、填空11.412.13.814.15.16.6
三、解答
17.∵垂直平分,
∴,,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
18.解:证明:
是边上的高
平分
19.(1)∵平分,
∴,
即:
(2)由AC的延长线与射线BE相交于一点F知与不平行,
∵是的外角,
∴,
∵平分,
∴
∵
∴
又
∴
∴
(3)设过点C的直线交于点G,此时,均为等腰三角形,
①当时,则有,,,
又,
②当时,,
,
,
,
③当时,
,
故此情况不存在,
④当,时,,,
,
,
又且
,
;
⑤当时,则,,
又,
∴
又
∴
解得,
故此情况不存在,
综上,的值为,或
20.(1)证明:∵ 和 都是等边三角形,
∴,,,
∴,即.
在△ABE 和△ADC 中
,
∴,
∴.
(2)证明:过点 A 分别作 ,,垂足为点 M,N.
∵由(1)知:,
∴
∴
∴
∴点 A 在的平分线上, 即 平分.
21.(1)∵
在与中
∴
(2)∵
∴
∵,
∴
∴
∴
∴
22.(1)解:∵,,
∴;
(2)如图1,在线段上截取,连接,
∵,,
∴是等边三角形,
∴
∵,
∴,
∴,
∴,
∵,
∴;
(3)延长交的延长线于点N,
由(2)及图1得,是等边三角形,
,
,
,
∴, 又,
∴,
∴,
∵既是的角平分线又是高,
,
∴是的中线,
即:,
.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
