沪科版数学七下8.2 整式乘法(第3课时)课件
文档属性
| 名称 | 沪科版数学七下8.2 整式乘法(第3课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 186.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-07 13:55:08 | ||
图片预览







文档简介
课件20张PPT。8.2整式乘法(第3课时)单项式与多项式相乘有理数的乘法单项式的乘法法则包括以下三部分:
(1)积的系数等于各因式系数的积;
(2)相同字母相乘;
(3)只在一个单项式里含有的字母,
要连同它的指数写在积里.
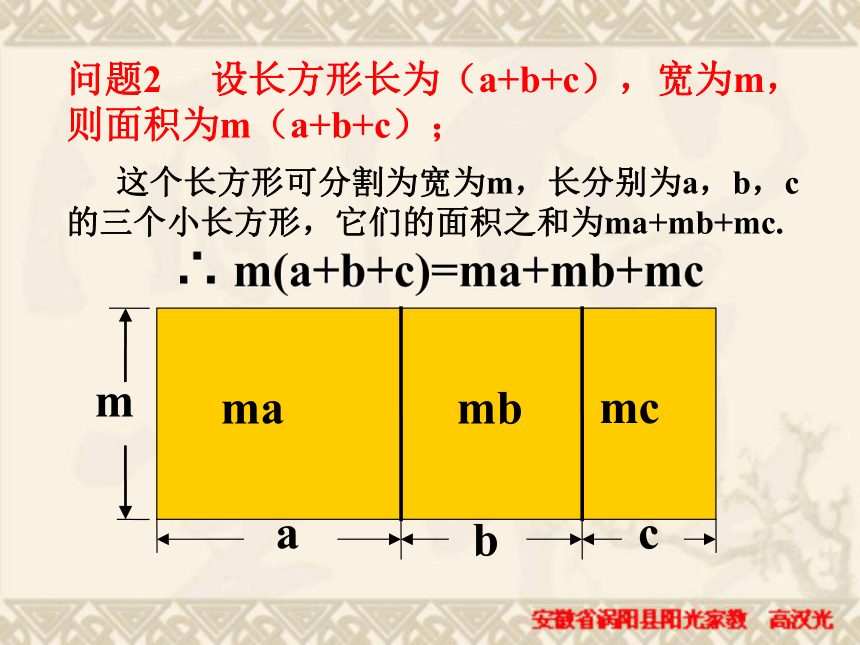
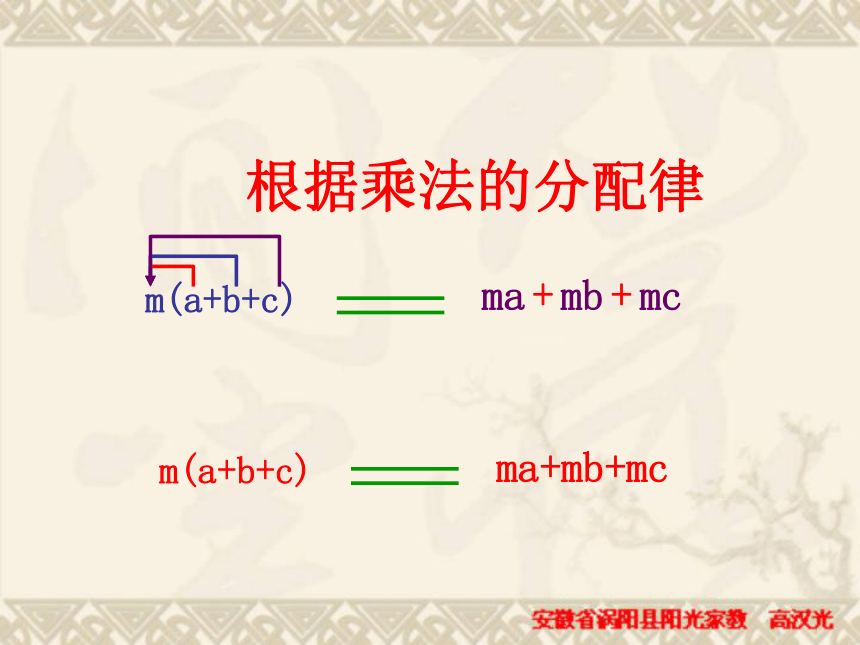
(注意 不要把这个因式丢掉)(同底数幂的乘法) 单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.单项式的乘法法则根据单项式乘单项式的法则填空:问题2 设长方形长为(a+b+c),宽为m,则面积为m(a+b+c); 这个长方形可分割为宽为m,长分别为a,b,c的三个小长方形,它们的面积之和为ma+mb+mc. ∴ m(a+b+c)=ma+mb+mcm(a+b+c)mb+mcma+根据乘法的分配律 单项式与多项式相乘,就是依据乘法分配律,用单项式乘多项式的每一项,再把所得的积相加.单项式乘多项式的运算法则 单项式与多项式相乘,就是依据乘法分配律,用单项式乘多项式的每一项,再把所得的积相加.例1 计算:
⑴ (-3a) ·(-2a2-3a-2)解:(-3a) ·(-2a2-3a-2)
=(-3a) ·(-2a2)+(-3a) ·(-3a)+(-3a) ·(-2)
=6a3+9a2+6a乘法分配率单项式乘单项式运算法则1.单项式与多项式相乘,就是用单项式去乘
多项式的________,再把所得的积________2.4(a-b+1)=___________________每一项相加4a-4b+43.3x(2x-y2)=___________________6x2-3xy24.-3x(2x-5y+6z)=___________________-6x2+15xy-18xz5.(-2a2)2(-a-2b+c)=___________________-4a5-8a4b+4a4c填一填(-2a)?(2a2-3a+1)=(-2a)?2a2+(-2a)?(-3a)+(-2a)?1=-4a3+6a2-2a(乘法分配律)(单项式与单项式相乘)练一练例2 计算:-2a2·(ab+b2)-5a(a2b-ab2) 解:原式=-a3b-2a2b2-5a3b+5a2b2=-a3b-2a2b2-5a3b+5a2b2注意:
1.将2a2与5a前面的“-”看成性质符号
2.单项式与多项式相乘的结果中,应将同类项合并。 =-6a3b+3a2b2 例3:如图:一块长方形地用来建造住宅、广场、商厦,求这块地的面积.解:长方形的长为(3a+2b)+(2a-b),宽为4a,这块地的面积为:4a[(3a+2b)+(2a-b)]
=4a(5a+b)
=4a·5a+4a·b
=20a2+4ab.
答:这块地的面积为20a2+4ab.计算:(4)(3x2y-xy2)·(-3xy) 计算:
(1) (-3x2)·(4x-3)
(2) (3)
(4)
巩固练习:yn(yn +9y-12)–3(3yn+1-4yn),
其中y=-3,n=2.解:yn(yn + 9y-12)–3(3yn+1-4yn)=y2n+9yn+1-12yn–9yn+1+12yn=y2n当y=-3,n=2时,原式=(-3)2×2=(-3)4=81例4:化简求值:7x-(x–3)x–3x(2–x)=(2x+1)x+6解:去括号,得
7x–x2+3x–6x+3x2=2x2+x+6移项,得
7x–x2+3x–6x+3x2-2x2-x=6合并同类项,得 3x = 6系数化为1,得 x = 2 例5:解方程1.已知:xy2=-2,求-xy(x3y7-3x2y5-y)延伸拓展:3.已知M,N分别表示不同的单项式,且3x(M-5x)=6x2y3+N,求M,N. 2.已知A=-3xy2,B=2xy(x-y),求A·B延伸拓展: 1.单项式与多项式相乘的依据是乘法对加法的分配律.
2.单项式与多项式相乘,其积仍是多项式,项数与原多项式的项数相同,注意不要漏乘项.
3.积的每一项的符号由原多项式各项符号和单项式的符号来决定,注意运用去括号法则.小结:
(1)积的系数等于各因式系数的积;
(2)相同字母相乘;
(3)只在一个单项式里含有的字母,
要连同它的指数写在积里.
(注意 不要把这个因式丢掉)(同底数幂的乘法) 单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.单项式的乘法法则根据单项式乘单项式的法则填空:问题2 设长方形长为(a+b+c),宽为m,则面积为m(a+b+c); 这个长方形可分割为宽为m,长分别为a,b,c的三个小长方形,它们的面积之和为ma+mb+mc. ∴ m(a+b+c)=ma+mb+mcm(a+b+c)mb+mcma+根据乘法的分配律 单项式与多项式相乘,就是依据乘法分配律,用单项式乘多项式的每一项,再把所得的积相加.单项式乘多项式的运算法则 单项式与多项式相乘,就是依据乘法分配律,用单项式乘多项式的每一项,再把所得的积相加.例1 计算:
⑴ (-3a) ·(-2a2-3a-2)解:(-3a) ·(-2a2-3a-2)
=(-3a) ·(-2a2)+(-3a) ·(-3a)+(-3a) ·(-2)
=6a3+9a2+6a乘法分配率单项式乘单项式运算法则1.单项式与多项式相乘,就是用单项式去乘
多项式的________,再把所得的积________2.4(a-b+1)=___________________每一项相加4a-4b+43.3x(2x-y2)=___________________6x2-3xy24.-3x(2x-5y+6z)=___________________-6x2+15xy-18xz5.(-2a2)2(-a-2b+c)=___________________-4a5-8a4b+4a4c填一填(-2a)?(2a2-3a+1)=(-2a)?2a2+(-2a)?(-3a)+(-2a)?1=-4a3+6a2-2a(乘法分配律)(单项式与单项式相乘)练一练例2 计算:-2a2·(ab+b2)-5a(a2b-ab2) 解:原式=-a3b-2a2b2-5a3b+5a2b2=-a3b-2a2b2-5a3b+5a2b2注意:
1.将2a2与5a前面的“-”看成性质符号
2.单项式与多项式相乘的结果中,应将同类项合并。 =-6a3b+3a2b2 例3:如图:一块长方形地用来建造住宅、广场、商厦,求这块地的面积.解:长方形的长为(3a+2b)+(2a-b),宽为4a,这块地的面积为:4a[(3a+2b)+(2a-b)]
=4a(5a+b)
=4a·5a+4a·b
=20a2+4ab.
答:这块地的面积为20a2+4ab.计算:(4)(3x2y-xy2)·(-3xy) 计算:
(1) (-3x2)·(4x-3)
(2) (3)
(4)
巩固练习:yn(yn +9y-12)–3(3yn+1-4yn),
其中y=-3,n=2.解:yn(yn + 9y-12)–3(3yn+1-4yn)=y2n+9yn+1-12yn–9yn+1+12yn=y2n当y=-3,n=2时,原式=(-3)2×2=(-3)4=81例4:化简求值:7x-(x–3)x–3x(2–x)=(2x+1)x+6解:去括号,得
7x–x2+3x–6x+3x2=2x2+x+6移项,得
7x–x2+3x–6x+3x2-2x2-x=6合并同类项,得 3x = 6系数化为1,得 x = 2 例5:解方程1.已知:xy2=-2,求-xy(x3y7-3x2y5-y)延伸拓展:3.已知M,N分别表示不同的单项式,且3x(M-5x)=6x2y3+N,求M,N. 2.已知A=-3xy2,B=2xy(x-y),求A·B延伸拓展: 1.单项式与多项式相乘的依据是乘法对加法的分配律.
2.单项式与多项式相乘,其积仍是多项式,项数与原多项式的项数相同,注意不要漏乘项.
3.积的每一项的符号由原多项式各项符号和单项式的符号来决定,注意运用去括号法则.小结:
