沪科版数学七下8.2 整式乘法(第5课时)课件
文档属性
| 名称 | 沪科版数学七下8.2 整式乘法(第5课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 280.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-07 13:58:36 | ||
图片预览






文档简介
课件20张PPT。8.2整式乘法(第5课时)多项式与多项式相乘② 再把所得的积相加。① 将单项式分别乘以多项式的各项,① 不能漏乘:即单项式要乘多项式的每一项② 去括号时注意符号的确定.复习(1)(-3x3y)(-5x4y2z4)=_______;
(2)-3ab2(-4a+3ab-2)
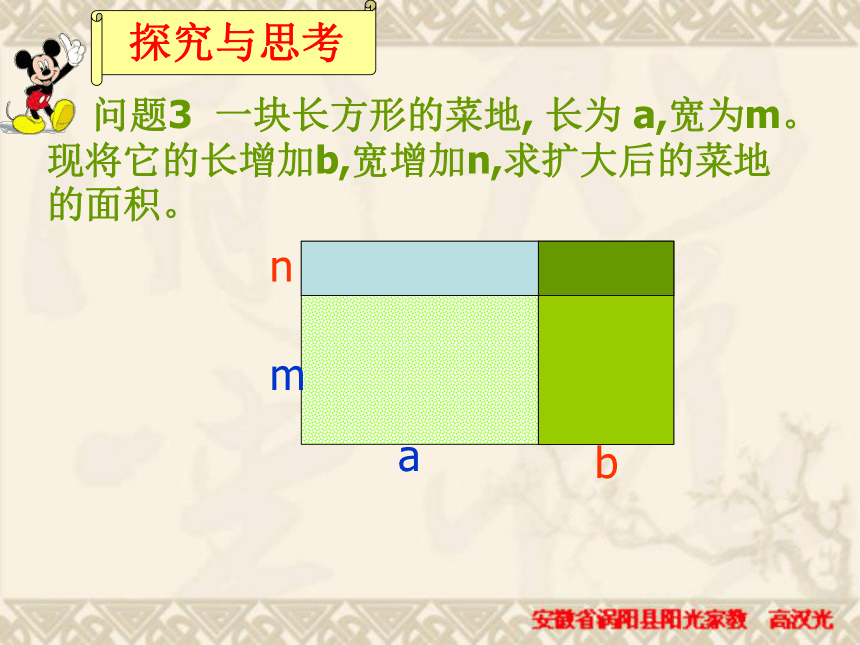
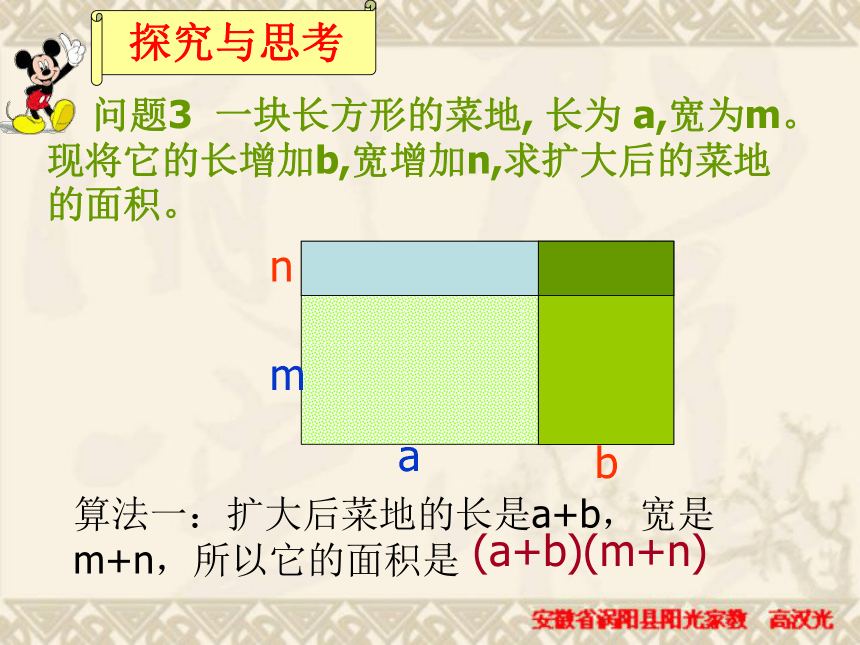
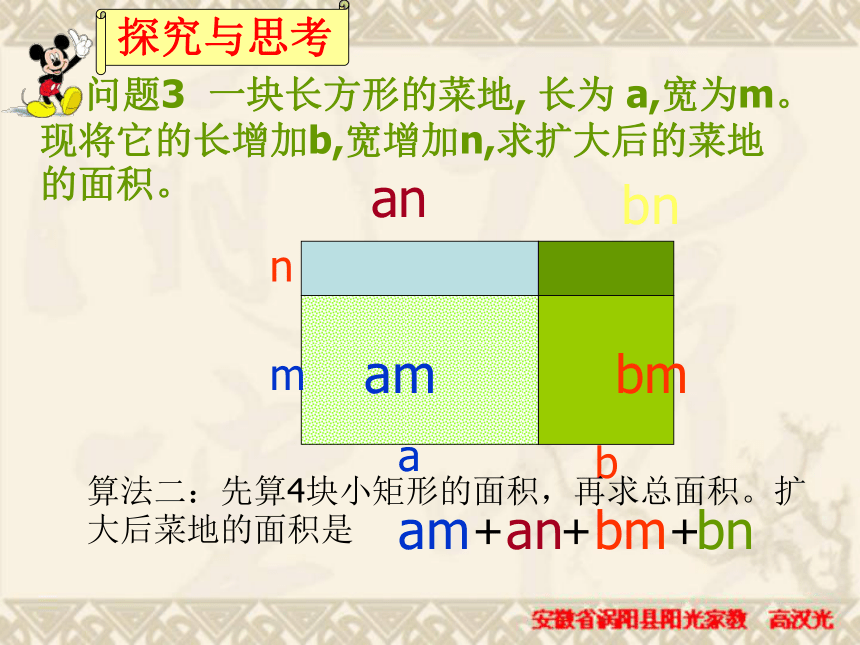
=________________15x7y3z412a2b2-9a2b3+6ab2练习 问题3 一块长方形的菜地, 长为 a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。nbma探究与思考 问题3 一块长方形的菜地, 长为 a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。nbma(a+b)(m+n)算法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是 问题3 一块长方形的菜地, 长为 a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。maamanbmbnamanbmbn+++算法二:先算4块小矩形的面积,再求总面积。扩大后菜地的面积是 由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=ma+ mb+ na+ nb如何进行多项式与多项式相乘的运算 ?实际上,把(m+n)看成一个整体,有:= ma+mb+na+nb(m+n)(a+b)= (m+n)a+(m+n)b (a+b)(m+n)=am+an+bm+bn多项式的乘法法则例题解析 【例1】计算: (1)(x+2)(x?3), (2)(3x -1)(2x+1)。===注意:1、两项相乘时先定符号,积的符号由这两
项的符号决定。同号得正,异号得负。
2、最后的结果要合并同类项。例题解析 【例1】计算: (1)(x+2)(x?3), (2)(3x -1)(2x+1)。==注意:1、两项相乘时先定符号,积的符号由这两
项的符号决定。同号得正,异号得负。
2、最后的结果要合并同类项。(2) (3x -1)(2x+1)3x?2x+3x? 1-1?2 x?16x2 +x?1.(1)(x+y)(a+2b); (2) (3x-1)(x+3)注意:多项式与多项式相乘的结果中,要把同类项合并.解:原式解:原式 【例2】计算: 【例3】计算: (1)(x?3y)(x+7y) (2)(2x + 5y)(3x?2y)+7xy?3yx-=x2 +4xy-21y2; 21y2(2) (2x +5 y)(3x?2y)==x22x?3x ?2x? 2y +5 y? 3x?5y?2y=6x2?4xy+ 15xy?10y2=6x2 +11xy?10y2.填空:
(1)(2x+y)(x-y)=__________.
(2)(m+2n)(m-2n)=________.
(3)(2m+5)(2m-3)=_____________.
(4)(1-x)(0.6-x)=____________.
(5)(x+2y)(x+8y)=____________.2x2-xy-y2m2-4n24m2+10m-15x2-1.6x+0.6x2+10xy+16y2练习 (1)(x?3y)(x+7y)
(2)(2x + 5y)(3x?2y)(3)(4) (m+2n)(m?2n);
(5) (2n +5)(n?3) ;巩固练习 观察下列各式计算结果与相乘的两个多项式之间的关系,你能发现什么规律?解:原式(1) (xy–z)(2xy+z) ;(2) (x–1)(x2+x+1) ;(3) (2a+b)2;(4) (3a–2)(a–1)–(a+1)(a+2) ;达标练习1.解方程(不等式):
(1)(3x-2)(2x-3)=(6x+5)(x-1)-1
(2)(x-2)(x+3) =(x+2)(x-5)
2.先化简,再求值.
6x2-(2x+1)(3x-2)+(x+3)(x-3),其中
x=(4)(x + y)(2x2y - 4xy2)
(5)(2x + 1)(4x2 - 2 x + 1)作业本节课你的收获是什么?本节课你学到了什么?合并同类项.
(2)-3ab2(-4a+3ab-2)
=________________15x7y3z412a2b2-9a2b3+6ab2练习 问题3 一块长方形的菜地, 长为 a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。nbma探究与思考 问题3 一块长方形的菜地, 长为 a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。nbma(a+b)(m+n)算法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是 问题3 一块长方形的菜地, 长为 a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。maamanbmbnamanbmbn+++算法二:先算4块小矩形的面积,再求总面积。扩大后菜地的面积是 由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=ma+ mb+ na+ nb如何进行多项式与多项式相乘的运算 ?实际上,把(m+n)看成一个整体,有:= ma+mb+na+nb(m+n)(a+b)= (m+n)a+(m+n)b (a+b)(m+n)=am+an+bm+bn多项式的乘法法则例题解析 【例1】计算: (1)(x+2)(x?3), (2)(3x -1)(2x+1)。===注意:1、两项相乘时先定符号,积的符号由这两
项的符号决定。同号得正,异号得负。
2、最后的结果要合并同类项。例题解析 【例1】计算: (1)(x+2)(x?3), (2)(3x -1)(2x+1)。==注意:1、两项相乘时先定符号,积的符号由这两
项的符号决定。同号得正,异号得负。
2、最后的结果要合并同类项。(2) (3x -1)(2x+1)3x?2x+3x? 1-1?2 x?16x2 +x?1.(1)(x+y)(a+2b); (2) (3x-1)(x+3)注意:多项式与多项式相乘的结果中,要把同类项合并.解:原式解:原式 【例2】计算: 【例3】计算: (1)(x?3y)(x+7y) (2)(2x + 5y)(3x?2y)+7xy?3yx-=x2 +4xy-21y2; 21y2(2) (2x +5 y)(3x?2y)==x22x?3x ?2x? 2y +5 y? 3x?5y?2y=6x2?4xy+ 15xy?10y2=6x2 +11xy?10y2.填空:
(1)(2x+y)(x-y)=__________.
(2)(m+2n)(m-2n)=________.
(3)(2m+5)(2m-3)=_____________.
(4)(1-x)(0.6-x)=____________.
(5)(x+2y)(x+8y)=____________.2x2-xy-y2m2-4n24m2+10m-15x2-1.6x+0.6x2+10xy+16y2练习 (1)(x?3y)(x+7y)
(2)(2x + 5y)(3x?2y)(3)(4) (m+2n)(m?2n);
(5) (2n +5)(n?3) ;巩固练习 观察下列各式计算结果与相乘的两个多项式之间的关系,你能发现什么规律?解:原式(1) (xy–z)(2xy+z) ;(2) (x–1)(x2+x+1) ;(3) (2a+b)2;(4) (3a–2)(a–1)–(a+1)(a+2) ;达标练习1.解方程(不等式):
(1)(3x-2)(2x-3)=(6x+5)(x-1)-1
(2)(x-2)(x+3) =(x+2)(x-5)
2.先化简,再求值.
6x2-(2x+1)(3x-2)+(x+3)(x-3),其中
x=(4)(x + y)(2x2y - 4xy2)
(5)(2x + 1)(4x2 - 2 x + 1)作业本节课你的收获是什么?本节课你学到了什么?合并同类项.
