2022—2023学年华东师大版数学七年级下册第九章 多边形 同步练习(含答案)
文档属性
| 名称 | 2022—2023学年华东师大版数学七年级下册第九章 多边形 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 888.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 08:09:36 | ||
图片预览


文档简介
华师大版七下 多边形 单元综合练
一、选择题(共9小题)
1. 下列图形中具有稳定性的是
A. 正方形 B. 矩形 C. 平行四边形 D. 直角三角形
2. 在 中,若 ,则 是
A. 锐角三角形 B. 钝角三角形 C. 等腰三角形 D. 直角三角形
3. 在正三角形,正方形,正五边形,正六边形这几个图形中,单独选用一种图形不能进行平面镶嵌的图形是
A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形
4. 已知三角形的两边长分别为 和 ,则下列长度的四条线段中能作为第三边的是
A. B. C. D.
5. 如图,在 中, 是 的平分线, 是外角 的平分线, 与 相交于点 ,若 ,则 等于
A. B. C. D.
6. 有下列条件:① ;② ;③ ;④ .其中能确定 是直角三角形的有
A. 个 B. 个 C. 个 D. 个
7. 从某多边形的一个顶点出发,可以作 条对角线,则该多边形是
A. 五边形 B. 六边形 C. 七边形 D. 八边形
8. 若一个多边形的内角和是其外角和的两倍,则它的边数是
A. 四 B. 五 C. 六 D. 七
9. 一幅美丽的图案,在某个顶点处由四个边长相等的正多边形镶嵌而成,其中的三个分别为正三角形、正方形、正六边形,那么另外一个是
A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形
二、填空题(共6小题)
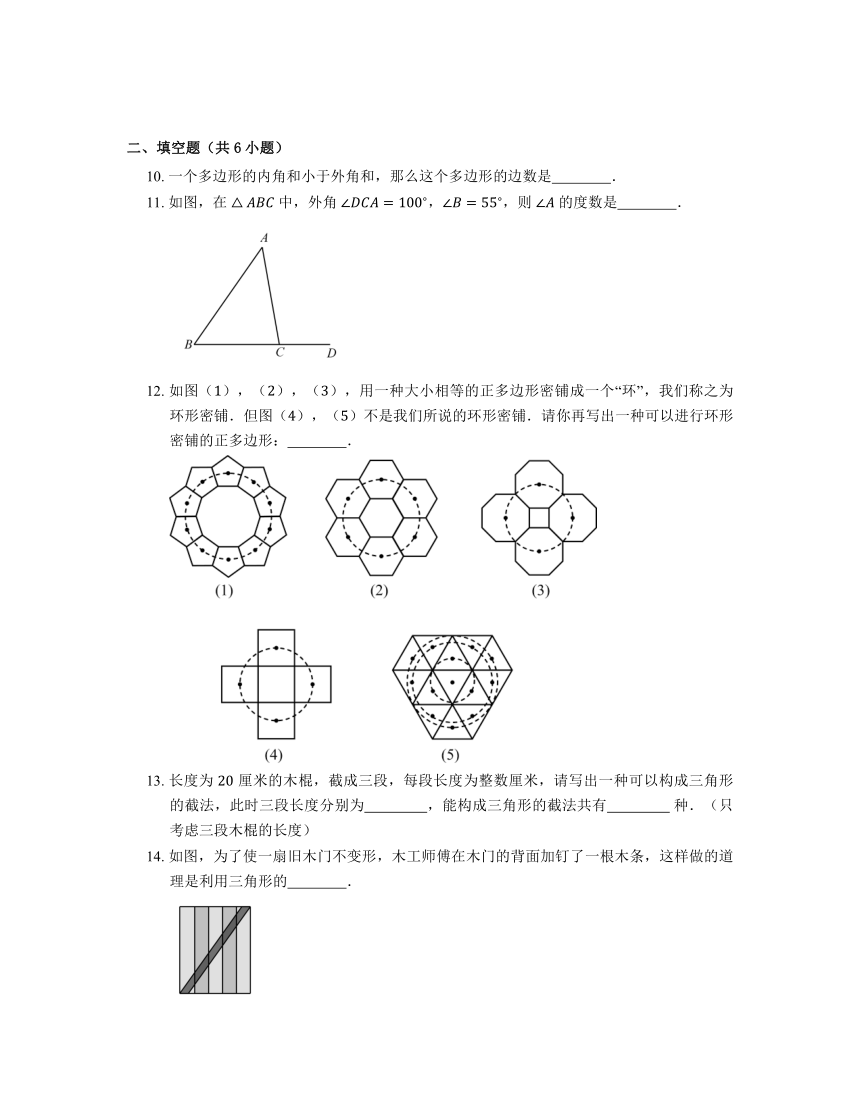
10. 一个多边形的内角和小于外角和,那么这个多边形的边数是 .
11. 如图,在 中,外角 ,,则 的度数是 .
12. 如图(),(),(),用一种大小相等的正多边形密铺成一个“环”,我们称之为环形密铺.但图(),()不是我们所说的环形密铺.请你再写出一种可以进行环形密铺的正多边形: .
13. 长度为 厘米的木棍,截成三段,每段长度为整数厘米,请写出一种可以构成三角形的截法,此时三段长度分别为 ,能构成三角形的截法共有 种.(只考虑三段木棍的长度)
14. 如图,为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是利用三角形的 .
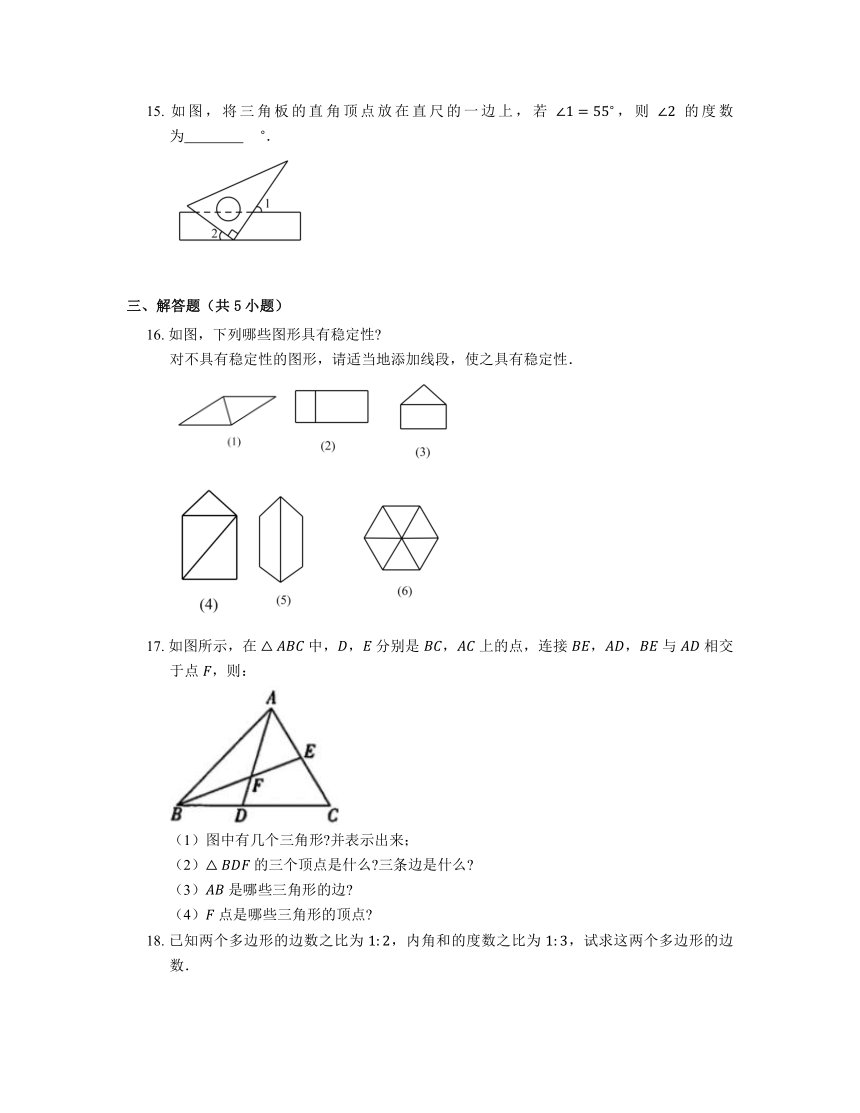
15. 如图,将三角板的直角顶点放在直尺的一边上,若 ,则 的度数为 .
三、解答题(共5小题)
16. 如图,下列哪些图形具有稳定性
对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
17. 如图所示,在 中,, 分别是 , 上的点,连接 ,, 与 相交于点 ,则:
(1)图中有几个三角形 并表示出来;
(2) 的三个顶点是什么 三条边是什么
(3) 是哪些三角形的边
(4) 点是哪些三角形的顶点
18. 已知两个多边形的边数之比为 ,内角和的度数之比为 ,试求这两个多边形的边数.
19. 如图,在 中,,, 的平分线相交于点 ,过点 分别作 ,,交 于点 ,,求 的度数.
20. (1)如图,延长凸五边形 的各边得五个角, 、 、 、 、 ,求 的度数;
(2)若延长凸 边形 的各边得 个角,则得到 个角的和等于 .
答案
1. D
2. B
3. C
4. B
5. B
【解析】,
.
又 ,
.
6. D
7. B
8. C 【解析】设这个多边形的边数为 ,
根据题意,得 ,
解得:.
故这个多边形的边数为 .
9. B
【解析】因为正三角形、正方形、正六边形的内角分别为 ,,,又因为 ,所以另外一个多边形为正方形.
10.
11.
12. 正十二边形
13. 厘米, 厘米, 厘米(答案不唯一,下述 种中的一种即可),
【解析】设其中两端木棍的长度分别为 ,,则第三段木棍长为 ,且 , 均为正整数,
根据三角形三边长的关系可知:两边之和大于第三边,两边之差小于第三边,
则 ,,,
所以 ,,,
当 时,,不符合题意;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为 厘米, 厘米, 厘米;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
综上所述:可以组成三角形的三段木棍长分别为:① ,,;② ,,;③ ,,;④ ,,;⑤ ,,;⑥ ,,;⑦ ,,;⑧ ,,.
14. 稳定性
15.
16. (1)(4)(6)具有稳定性,如图即为所求.
17. (1) 图中共有 个三角形,分别是 ,,,,,,,.
(2) 的三个顶点是 ,,,三条边是 ,,.
(3) 是 ,,, 的边.
(4) 点是 ,, 的顶点.
18. 这两个多边形的边数分别是 和 ( 是正整数).
根据题意,得
也就是
解得
所以这两个多边形的边数分别为 和 .
19. .
20. (1)
连接 并延长至 .
,,
.
即 .
,
.
.
.
(2) .
【解析】
当 时,连接 ,,,,.
以此类推:
若延长凸 边形 的各边得 个角,
则得到 个角的和 .
一、选择题(共9小题)
1. 下列图形中具有稳定性的是
A. 正方形 B. 矩形 C. 平行四边形 D. 直角三角形
2. 在 中,若 ,则 是
A. 锐角三角形 B. 钝角三角形 C. 等腰三角形 D. 直角三角形
3. 在正三角形,正方形,正五边形,正六边形这几个图形中,单独选用一种图形不能进行平面镶嵌的图形是
A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形
4. 已知三角形的两边长分别为 和 ,则下列长度的四条线段中能作为第三边的是
A. B. C. D.
5. 如图,在 中, 是 的平分线, 是外角 的平分线, 与 相交于点 ,若 ,则 等于
A. B. C. D.
6. 有下列条件:① ;② ;③ ;④ .其中能确定 是直角三角形的有
A. 个 B. 个 C. 个 D. 个
7. 从某多边形的一个顶点出发,可以作 条对角线,则该多边形是
A. 五边形 B. 六边形 C. 七边形 D. 八边形
8. 若一个多边形的内角和是其外角和的两倍,则它的边数是
A. 四 B. 五 C. 六 D. 七
9. 一幅美丽的图案,在某个顶点处由四个边长相等的正多边形镶嵌而成,其中的三个分别为正三角形、正方形、正六边形,那么另外一个是
A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形
二、填空题(共6小题)
10. 一个多边形的内角和小于外角和,那么这个多边形的边数是 .
11. 如图,在 中,外角 ,,则 的度数是 .
12. 如图(),(),(),用一种大小相等的正多边形密铺成一个“环”,我们称之为环形密铺.但图(),()不是我们所说的环形密铺.请你再写出一种可以进行环形密铺的正多边形: .
13. 长度为 厘米的木棍,截成三段,每段长度为整数厘米,请写出一种可以构成三角形的截法,此时三段长度分别为 ,能构成三角形的截法共有 种.(只考虑三段木棍的长度)
14. 如图,为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是利用三角形的 .
15. 如图,将三角板的直角顶点放在直尺的一边上,若 ,则 的度数为 .
三、解答题(共5小题)
16. 如图,下列哪些图形具有稳定性
对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
17. 如图所示,在 中,, 分别是 , 上的点,连接 ,, 与 相交于点 ,则:
(1)图中有几个三角形 并表示出来;
(2) 的三个顶点是什么 三条边是什么
(3) 是哪些三角形的边
(4) 点是哪些三角形的顶点
18. 已知两个多边形的边数之比为 ,内角和的度数之比为 ,试求这两个多边形的边数.
19. 如图,在 中,,, 的平分线相交于点 ,过点 分别作 ,,交 于点 ,,求 的度数.
20. (1)如图,延长凸五边形 的各边得五个角, 、 、 、 、 ,求 的度数;
(2)若延长凸 边形 的各边得 个角,则得到 个角的和等于 .
答案
1. D
2. B
3. C
4. B
5. B
【解析】,
.
又 ,
.
6. D
7. B
8. C 【解析】设这个多边形的边数为 ,
根据题意,得 ,
解得:.
故这个多边形的边数为 .
9. B
【解析】因为正三角形、正方形、正六边形的内角分别为 ,,,又因为 ,所以另外一个多边形为正方形.
10.
11.
12. 正十二边形
13. 厘米, 厘米, 厘米(答案不唯一,下述 种中的一种即可),
【解析】设其中两端木棍的长度分别为 ,,则第三段木棍长为 ,且 , 均为正整数,
根据三角形三边长的关系可知:两边之和大于第三边,两边之差小于第三边,
则 ,,,
所以 ,,,
当 时,,不符合题意;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为 厘米, 厘米, 厘米;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
当 时,,
即 ,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
,,三段长度分别为: 厘米, 厘米, 厘米;
综上所述:可以组成三角形的三段木棍长分别为:① ,,;② ,,;③ ,,;④ ,,;⑤ ,,;⑥ ,,;⑦ ,,;⑧ ,,.
14. 稳定性
15.
16. (1)(4)(6)具有稳定性,如图即为所求.
17. (1) 图中共有 个三角形,分别是 ,,,,,,,.
(2) 的三个顶点是 ,,,三条边是 ,,.
(3) 是 ,,, 的边.
(4) 点是 ,, 的顶点.
18. 这两个多边形的边数分别是 和 ( 是正整数).
根据题意,得
也就是
解得
所以这两个多边形的边数分别为 和 .
19. .
20. (1)
连接 并延长至 .
,,
.
即 .
,
.
.
.
(2) .
【解析】
当 时,连接 ,,,,.
以此类推:
若延长凸 边形 的各边得 个角,
则得到 个角的和 .
