华师大版数学八年级下第19章矩形、菱形、正方形提高训练题(附答案解析)
文档属性
| 名称 | 华师大版数学八年级下第19章矩形、菱形、正方形提高训练题(附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 227.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-06 20:41:57 | ||
图片预览



文档简介
第19章 矩形、菱形、正方形提高训练题
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共30分)
1.如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( )21世纪教育网版权所有
A.14 B.15 C.16 D.17
2.下列命题中,正确的是( )
A.两条对角线相等的四边形是平行四边形
B.两条对角线相等且互相垂直的四边形是矩形
C.两条对角线互相垂直平分的四边形是菱形
D.两条对角线互相平分且相等的四边形是正方形
3.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN,若四边形MBND是菱形,则等于( )www.21-cn-jy.com
A. B. C. D.
4.如图,将矩形ABCD沿对角线BD折叠,使点C与点C′重合.若AB=2,则的长为( )【来源:21cnj*y.co*m】
A.1 B.2 C.3 D.4
5.已知:如图,在矩形ABCD中,E、F、G、H分别为边AB、DA、CD、BC的中点.若,,则图中阴影部分的面积为( )【版权所有:21教育】
A.3 B.4 C.6 D.8
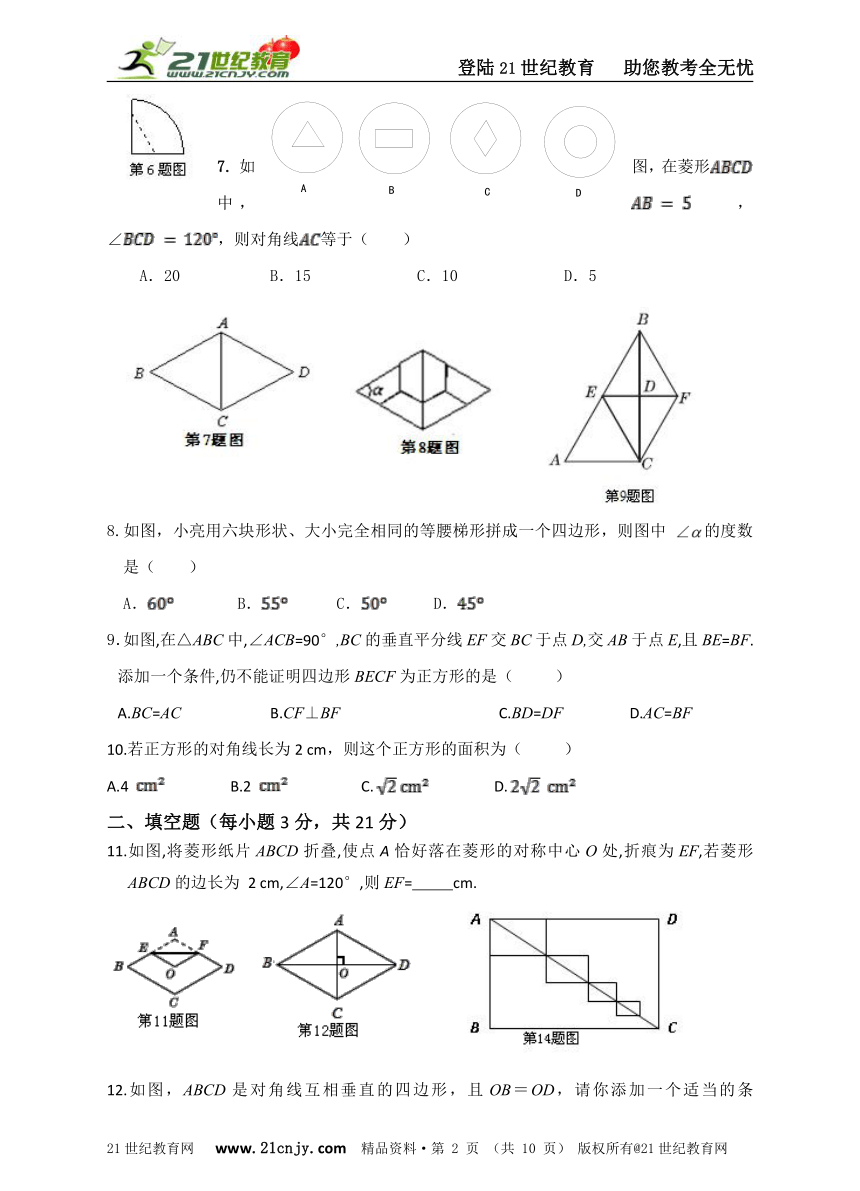
6.如图所示,将一圆形纸片对折后再对折,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是( )21教育网
7.如图,在菱形中,,∠,则对角线等于( )
A.20 B.15 C.10 D.5
8.如图,小亮用六块形状、大小完全相同的等腰梯形拼成一个四边形,则图中 的度数是( )
A. B. C. D.
9.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF为正方形的是( )21cnjy.com
A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF
10.若正方形的对角线长为2 cm,则这个正方形的面积为( )
A.4 B.2 C. D.
二、填空题(每小题3分,共21分)
11.如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为 2 cm,∠A=120°,则EF= cm.21*cnjy*com
12.如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 ,使ABCD成为菱形.(只需添加一个即可)21教育名师原创作品
13.已知菱形的边长为5,一条对角线长为8,则另一条对角线长为_________.
14.如图,矩形的对角线,,则图中五个小矩形的周长之和为_______.
15.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为 .
16.如图,在矩形ABCD中,对角线AC与BD相交于点O,且 cm,则BD的长为________cm,BC的长为_______cm.
17.如图,在矩形ABCD中,点E,F分别是AB,CD的中点,连接DE和BF,分别取DE,BF的中点M,N,连接AM,CN,MN,若AB=2,BC=2,则图中阴影部分的面积为 .
三、解答题(共49分)
18.(8分)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
19.(8分)已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且.请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并说明它和图中已有的某一条线段相等(只需说明一组线段相等即可):
(1)连接____________ ;
(2)猜想:______________=_______________;
(3)试证明你的猜想.
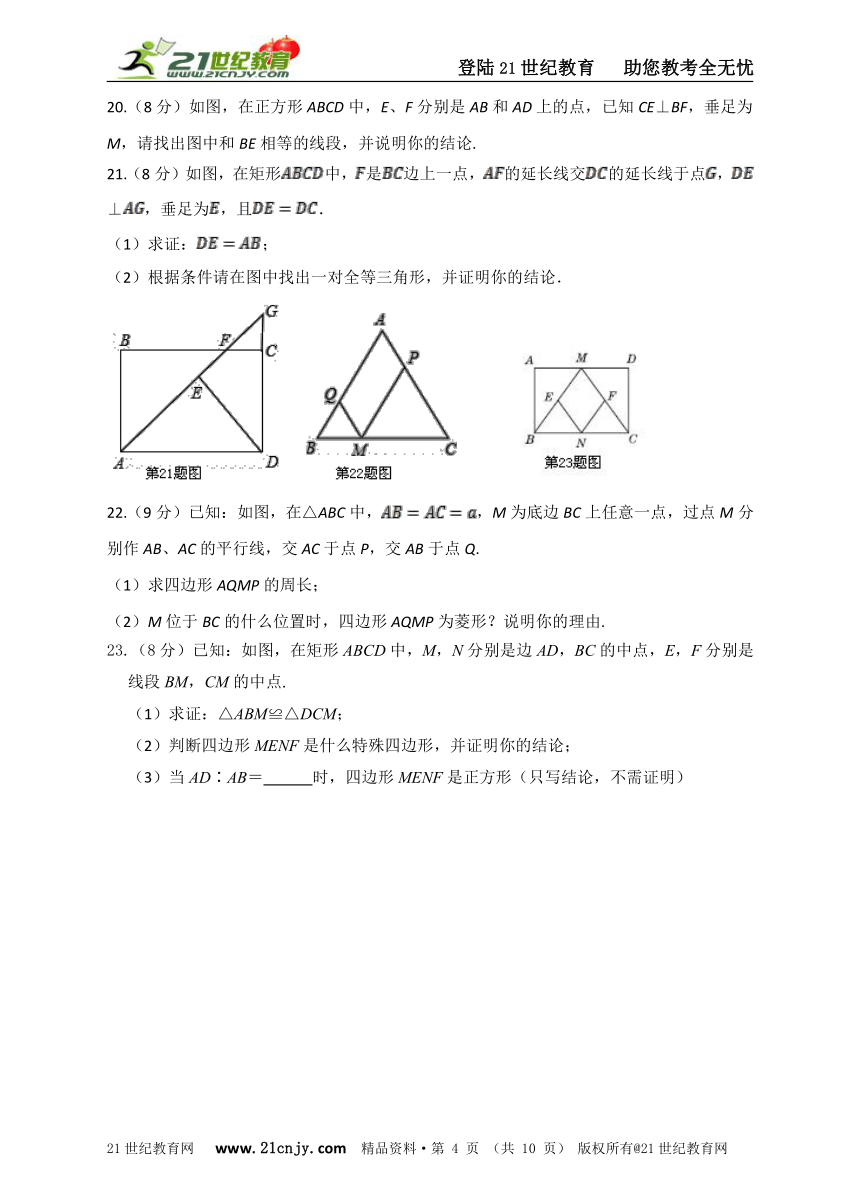
20.(8分)如图,在正方形ABCD中,E、F分别是AB和AD上的点,已知CE⊥BF,垂足为M,请找出图中和BE相等的线段,并说明你的结论.【来源:21·世纪·教育·网】
21.(8分)如图,在矩形中,是边上一点,的延长线交的延长线于点,⊥,垂足为,且.
(1)求证:;
(2)根据条件请在图中找出一对全等三角形,并证明你的结论.
22.(9分)已知:如图,在△ABC中,,M为底边BC上任意一点,过点M分别作AB、AC的平行线,交AC于点P,交AB于点Q.
(1)求四边形AQMP的周长;
(2)M位于BC的什么位置时,四边形AQMP为菱形?说明你的理由.
23.(8分)已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD∶AB= 时,四边形MENF是正方形(只写结论,不需证明)
第19章 矩形、菱形、正方形提高训练题答案与解析
1.C
解析:根据菱形的性质得到AB=BC=4,由∠B=60°得到△ABC是等边三角形,所以AC=4.则以AC为边长的正方形ACEF的周长为16.
2.C
解析:两条对角线互相平分的四边形是平行四边形,A错;
两条对角线互相平分且相等的四边形是矩形,B错;
两条对角线互相垂直平分且相等的四边形是正方形,D错.故选C.
3. C
解析:设AB=x,AM=y,则BM=MD=2x-y.在Rt△ABM中,根据勾股定理有BM2=AB2+AM2,即(2x-y)2=x2+y2,整理得3x=4y,所以x=y,故== =.
4.B
解析:因为四边形ABCD是矩形,所以CD=AB=2.由于沿BD折叠后点C与点C′重合,所以=CD=2. 21*cnjy*com
5.B
解析:∵ 矩形ABCD的面积为,
∴ 阴影部分的面积为,故选B.
6.C
7.D
解析:在菱形中,由∠=?,得 ∠.又∵ ,
∴ △是等边三角形,∴ .
8.A
解析:观察图形,在等腰梯形的一个上底角顶点处有三个上底角,因而等腰梯形上底角等于,所以.
9. D
解析:本题综合考查了直角三角形、线段的垂直平分线的性质与菱形、正方形的判定方法等知识.因为EF垂直平分BC,所以BE=EC,BF=FC.又BE=BF,所以BE=EC=CF=FB,所以四边形BECF为菱形.如果BC=AC,那么∠ABC=90°÷2=45°,则∠EBF=90°,能证明四边形BECF为正方形.如果CF⊥BF,那么∠BFC=90°,能证明四边形BECF为正方形.如果BD=DF,那么BC=EF,能证明四边形BECF为正方形.当AC=BF时,可得AC=BE=EC=AE,此时∠ABC=30°,则∠EBF=60°,不能证明四边形BECF为正方形.
点拨:判定一个四边形是正方形一般有两种方法:一是先证明它是矩形,再证明一组邻边相等或证明对角线互相垂直;二是先证明它是菱形,再证明有一个角是直角或证明对角线相等.21·世纪*教育网
10.B
解析:如图,正方形ABCD中,,则,即,所以,所以正方形的面积为2 ,故选B.
11.
解析:本题综合考查了菱形的性质、勾股定理和三角形中位线的性质.连接BD,AC.
∵ 四边形ABCD是菱形,∴ AC⊥BD,AC平分∠BAD.∵ ∠BAD=120°,∴ ∠BAC=60°,∴ ∠ABO=90°-60°=30°.∵ ∠AOB=90°,∴ AO=AB=×2=1(cm).由勾股定理得BO= cm,∴ DO= cm.∵ 点A沿EF折叠后与O重合,∴ EF⊥AC,EF平分AO.∵ AC⊥BD,∴ EF∥BD,∴ EF为△ABD的中位线,∴ EF=BD=×(+)=(cm).2·1·c·n·j·y
12. OA=OC或AD=BC或AD∥BC或AB=BC等(答案不唯一)
解析:本题主要考查了菱形的判定方法,属于条件开放型题目.对角线互相垂直平分的四边形是菱形;四条边都相等的四边形是菱形;有一组邻边相等的平行四边形是菱形;对角线互相垂直的平行四边形是菱形.2-1-c-n-j-y
13.6
解析:∵ 菱形的两条对角线互相垂直平分,∴ 根据勾股定理,可求得另一条对角线长的一半为3,则另一条对角线长为6.【出处:21教育名师】
14.28
解析:由勾股定理得 ,又,,所以所以五个小矩形的周长之和为
15. 20
解析:本题考查了矩形的性质、三角形中位线的性质和勾股定理.在Rt△ABC中,因为AB=5,BC=AD=12,由勾股定理可得AC=13.因为O是矩形ABCD的对角线AC的中点,M是AD的中点,所以OM==2.5,=6.5,,所以四边形ABOM的周长=AB+BO+OM+MA=5+6.5+2.5+6=20.
解析:因为 cm,所以 cm.又因为,所以 cm.
,所以(cm).
17. 2
解析:在Rt△ADE中,M为DE中点,故S△AEM=S△ADM,所以S△AEM=S△AED,同理
S△BNC=S△BFC,S□DMNF=S□BEDF,所以S阴影=S矩形ABCD=AB·BC=×2×2=2.21·cn·jy·com
18.分析:本题考查了全等三角形和正方形的判定.
(1)根据SAS定理可证明△ABD≌△CBD,从而得∠ADB=∠CDB.
(2)先根据“有三个角是直角的四边形是矩形”证得四边形MPND是矩形,再根据“角平分线上的点到角两边的距离相等”得PM=PN,从而证得矩形MPND是正方形.
证明:(1)∵ BD平分∠ABC,
∴ ∠ABD=∠CBD.
又∵ BA=BC,BD=BD,
∴ △ABD≌△CBD.
∴ ∠ADB=∠CDB.
(2)∵ PM⊥AD,PN⊥CD,
∴ ∠PMD=∠PND=90°.
又∵ ∠ADC=90°,∴ 四边形MPND是矩形.
由(1)知∠ADB=∠CDB,又PM⊥AD,PN⊥CD,
∴ PM=PN.
∴ 四边形MPND是正方形.
点拨:(1)证明三角形全等是证明角相等或线段相等的常用方法;(2)因为角平分线上的点到角两边的距离相等,所以遇到角平分线和两条垂线段时通常考虑这两条垂线段 相等.www-2-1-cnjy-com
19.分析:观察图形可知应该是连接AF,可通过证△ABF和△ADE全等来实现.
解:(1)如图,连接AF.
(2).
(3)∵ 四边形ABCD是菱形,
∴ ,
∴ ∠∠,
∴ ∠∠.
在△ABF和△ADE中,
∴ △ABF≌△ADE,∴ .
20.解:和BE相等的线段是AF.理由如下:
因为四边形ABCD是正方形,
所以,∠∠°.
因为CE⊥BF,所以∠∠°.
又因为∠∠°,
所以∠∠.
在△AFB和△BEC中,
所以△≌△,所以.
21.(1)证明:在矩形ABCD中,,且,
∴ .
(2)解:△ABF≌△DEA.
证明如下:在矩形ABCD中,∵ BC∥AD,
∴ ∠∠.
∵ DE⊥AG,∴ ∠°.
∵ ∠°,∴ ∠∠.
又∵ ,∴ △ABF≌△DEA.
22.分析:(1)根据平行四边形的性质可得对应角相等,对应边相等,从而不难求得其周长;
(2)根据中位线的性质及菱形的判定说明.
解:(1)∵ AB∥MP,QM∥AC,
∴ 四边形APMQ是平行四边形,∠∠,∠∠.
∵ ,∴ ∠∠,
∴ ∠∠,∠∠.
∴ ,.
∴ 四边形AQMP的周长.
(2)当点M是BC的中点时,四边形APMQ是菱形,理由如下:
∵ 点M是BC的中点,AB∥MP,QM∥AC,
∴ QM,PM是三角形ABC的中位线.
∵ ,∴ .
又由(1)知四边形APMQ是平行四边形,
∴ 平行四边形APMQ是菱形.
23. 分析:本题考查了矩形的性质以及菱形和正方形的判定.
(1)用SAS证明△ABM和△DCM全等.
(2)先证四边形MENF是平行四边形,再证它的一组邻边ME和MF相等.
(3)由(2)得四边形MENF是菱形,当它是正方形时,只需使∠BMC是直角,则有∠AMB+ ∠CMD=90°.又∵ ∠AMB=∠CMD,∴ △AMB和△CMD都是等腰直角三角形.
(1)证明:∵ 四边形ABCD是矩形,
∴ ∠A=∠D=90°,AB=DC.
又∵ MA=MD,
∴ △ABM≌△DCM(SAS).
(2)解:四边形MENF是菱形.
理由:∵ CF=FM,CN=NB,
∴ FN∥MB.同理可得:EN∥MC,
∴ 四边形MENF是平行四边形.
∵ △ABM≌△DCM,
∴ MB=MC.
又∵ ME=MB,MF=MC,
∴ ME=MF.
∴ 平行四边形MENF是菱形.
(3)解:2∶1.
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共30分)
1.如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( )21世纪教育网版权所有
A.14 B.15 C.16 D.17
2.下列命题中,正确的是( )
A.两条对角线相等的四边形是平行四边形
B.两条对角线相等且互相垂直的四边形是矩形
C.两条对角线互相垂直平分的四边形是菱形
D.两条对角线互相平分且相等的四边形是正方形
3.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN,若四边形MBND是菱形,则等于( )www.21-cn-jy.com
A. B. C. D.
4.如图,将矩形ABCD沿对角线BD折叠,使点C与点C′重合.若AB=2,则的长为( )【来源:21cnj*y.co*m】
A.1 B.2 C.3 D.4
5.已知:如图,在矩形ABCD中,E、F、G、H分别为边AB、DA、CD、BC的中点.若,,则图中阴影部分的面积为( )【版权所有:21教育】
A.3 B.4 C.6 D.8
6.如图所示,将一圆形纸片对折后再对折,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是( )21教育网
7.如图,在菱形中,,∠,则对角线等于( )
A.20 B.15 C.10 D.5
8.如图,小亮用六块形状、大小完全相同的等腰梯形拼成一个四边形,则图中 的度数是( )
A. B. C. D.
9.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF为正方形的是( )21cnjy.com
A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF
10.若正方形的对角线长为2 cm,则这个正方形的面积为( )
A.4 B.2 C. D.
二、填空题(每小题3分,共21分)
11.如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为 2 cm,∠A=120°,则EF= cm.21*cnjy*com
12.如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 ,使ABCD成为菱形.(只需添加一个即可)21教育名师原创作品
13.已知菱形的边长为5,一条对角线长为8,则另一条对角线长为_________.
14.如图,矩形的对角线,,则图中五个小矩形的周长之和为_______.
15.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为 .
16.如图,在矩形ABCD中,对角线AC与BD相交于点O,且 cm,则BD的长为________cm,BC的长为_______cm.
17.如图,在矩形ABCD中,点E,F分别是AB,CD的中点,连接DE和BF,分别取DE,BF的中点M,N,连接AM,CN,MN,若AB=2,BC=2,则图中阴影部分的面积为 .
三、解答题(共49分)
18.(8分)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
19.(8分)已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且.请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并说明它和图中已有的某一条线段相等(只需说明一组线段相等即可):
(1)连接____________ ;
(2)猜想:______________=_______________;
(3)试证明你的猜想.
20.(8分)如图,在正方形ABCD中,E、F分别是AB和AD上的点,已知CE⊥BF,垂足为M,请找出图中和BE相等的线段,并说明你的结论.【来源:21·世纪·教育·网】
21.(8分)如图,在矩形中,是边上一点,的延长线交的延长线于点,⊥,垂足为,且.
(1)求证:;
(2)根据条件请在图中找出一对全等三角形,并证明你的结论.
22.(9分)已知:如图,在△ABC中,,M为底边BC上任意一点,过点M分别作AB、AC的平行线,交AC于点P,交AB于点Q.
(1)求四边形AQMP的周长;
(2)M位于BC的什么位置时,四边形AQMP为菱形?说明你的理由.
23.(8分)已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD∶AB= 时,四边形MENF是正方形(只写结论,不需证明)
第19章 矩形、菱形、正方形提高训练题答案与解析
1.C
解析:根据菱形的性质得到AB=BC=4,由∠B=60°得到△ABC是等边三角形,所以AC=4.则以AC为边长的正方形ACEF的周长为16.
2.C
解析:两条对角线互相平分的四边形是平行四边形,A错;
两条对角线互相平分且相等的四边形是矩形,B错;
两条对角线互相垂直平分且相等的四边形是正方形,D错.故选C.
3. C
解析:设AB=x,AM=y,则BM=MD=2x-y.在Rt△ABM中,根据勾股定理有BM2=AB2+AM2,即(2x-y)2=x2+y2,整理得3x=4y,所以x=y,故== =.
4.B
解析:因为四边形ABCD是矩形,所以CD=AB=2.由于沿BD折叠后点C与点C′重合,所以=CD=2. 21*cnjy*com
5.B
解析:∵ 矩形ABCD的面积为,
∴ 阴影部分的面积为,故选B.
6.C
7.D
解析:在菱形中,由∠=?,得 ∠.又∵ ,
∴ △是等边三角形,∴ .
8.A
解析:观察图形,在等腰梯形的一个上底角顶点处有三个上底角,因而等腰梯形上底角等于,所以.
9. D
解析:本题综合考查了直角三角形、线段的垂直平分线的性质与菱形、正方形的判定方法等知识.因为EF垂直平分BC,所以BE=EC,BF=FC.又BE=BF,所以BE=EC=CF=FB,所以四边形BECF为菱形.如果BC=AC,那么∠ABC=90°÷2=45°,则∠EBF=90°,能证明四边形BECF为正方形.如果CF⊥BF,那么∠BFC=90°,能证明四边形BECF为正方形.如果BD=DF,那么BC=EF,能证明四边形BECF为正方形.当AC=BF时,可得AC=BE=EC=AE,此时∠ABC=30°,则∠EBF=60°,不能证明四边形BECF为正方形.
点拨:判定一个四边形是正方形一般有两种方法:一是先证明它是矩形,再证明一组邻边相等或证明对角线互相垂直;二是先证明它是菱形,再证明有一个角是直角或证明对角线相等.21·世纪*教育网
10.B
解析:如图,正方形ABCD中,,则,即,所以,所以正方形的面积为2 ,故选B.
11.
解析:本题综合考查了菱形的性质、勾股定理和三角形中位线的性质.连接BD,AC.
∵ 四边形ABCD是菱形,∴ AC⊥BD,AC平分∠BAD.∵ ∠BAD=120°,∴ ∠BAC=60°,∴ ∠ABO=90°-60°=30°.∵ ∠AOB=90°,∴ AO=AB=×2=1(cm).由勾股定理得BO= cm,∴ DO= cm.∵ 点A沿EF折叠后与O重合,∴ EF⊥AC,EF平分AO.∵ AC⊥BD,∴ EF∥BD,∴ EF为△ABD的中位线,∴ EF=BD=×(+)=(cm).2·1·c·n·j·y
12. OA=OC或AD=BC或AD∥BC或AB=BC等(答案不唯一)
解析:本题主要考查了菱形的判定方法,属于条件开放型题目.对角线互相垂直平分的四边形是菱形;四条边都相等的四边形是菱形;有一组邻边相等的平行四边形是菱形;对角线互相垂直的平行四边形是菱形.2-1-c-n-j-y
13.6
解析:∵ 菱形的两条对角线互相垂直平分,∴ 根据勾股定理,可求得另一条对角线长的一半为3,则另一条对角线长为6.【出处:21教育名师】
14.28
解析:由勾股定理得 ,又,,所以所以五个小矩形的周长之和为
15. 20
解析:本题考查了矩形的性质、三角形中位线的性质和勾股定理.在Rt△ABC中,因为AB=5,BC=AD=12,由勾股定理可得AC=13.因为O是矩形ABCD的对角线AC的中点,M是AD的中点,所以OM==2.5,=6.5,,所以四边形ABOM的周长=AB+BO+OM+MA=5+6.5+2.5+6=20.
解析:因为 cm,所以 cm.又因为,所以 cm.
,所以(cm).
17. 2
解析:在Rt△ADE中,M为DE中点,故S△AEM=S△ADM,所以S△AEM=S△AED,同理
S△BNC=S△BFC,S□DMNF=S□BEDF,所以S阴影=S矩形ABCD=AB·BC=×2×2=2.21·cn·jy·com
18.分析:本题考查了全等三角形和正方形的判定.
(1)根据SAS定理可证明△ABD≌△CBD,从而得∠ADB=∠CDB.
(2)先根据“有三个角是直角的四边形是矩形”证得四边形MPND是矩形,再根据“角平分线上的点到角两边的距离相等”得PM=PN,从而证得矩形MPND是正方形.
证明:(1)∵ BD平分∠ABC,
∴ ∠ABD=∠CBD.
又∵ BA=BC,BD=BD,
∴ △ABD≌△CBD.
∴ ∠ADB=∠CDB.
(2)∵ PM⊥AD,PN⊥CD,
∴ ∠PMD=∠PND=90°.
又∵ ∠ADC=90°,∴ 四边形MPND是矩形.
由(1)知∠ADB=∠CDB,又PM⊥AD,PN⊥CD,
∴ PM=PN.
∴ 四边形MPND是正方形.
点拨:(1)证明三角形全等是证明角相等或线段相等的常用方法;(2)因为角平分线上的点到角两边的距离相等,所以遇到角平分线和两条垂线段时通常考虑这两条垂线段 相等.www-2-1-cnjy-com
19.分析:观察图形可知应该是连接AF,可通过证△ABF和△ADE全等来实现.
解:(1)如图,连接AF.
(2).
(3)∵ 四边形ABCD是菱形,
∴ ,
∴ ∠∠,
∴ ∠∠.
在△ABF和△ADE中,
∴ △ABF≌△ADE,∴ .
20.解:和BE相等的线段是AF.理由如下:
因为四边形ABCD是正方形,
所以,∠∠°.
因为CE⊥BF,所以∠∠°.
又因为∠∠°,
所以∠∠.
在△AFB和△BEC中,
所以△≌△,所以.
21.(1)证明:在矩形ABCD中,,且,
∴ .
(2)解:△ABF≌△DEA.
证明如下:在矩形ABCD中,∵ BC∥AD,
∴ ∠∠.
∵ DE⊥AG,∴ ∠°.
∵ ∠°,∴ ∠∠.
又∵ ,∴ △ABF≌△DEA.
22.分析:(1)根据平行四边形的性质可得对应角相等,对应边相等,从而不难求得其周长;
(2)根据中位线的性质及菱形的判定说明.
解:(1)∵ AB∥MP,QM∥AC,
∴ 四边形APMQ是平行四边形,∠∠,∠∠.
∵ ,∴ ∠∠,
∴ ∠∠,∠∠.
∴ ,.
∴ 四边形AQMP的周长.
(2)当点M是BC的中点时,四边形APMQ是菱形,理由如下:
∵ 点M是BC的中点,AB∥MP,QM∥AC,
∴ QM,PM是三角形ABC的中位线.
∵ ,∴ .
又由(1)知四边形APMQ是平行四边形,
∴ 平行四边形APMQ是菱形.
23. 分析:本题考查了矩形的性质以及菱形和正方形的判定.
(1)用SAS证明△ABM和△DCM全等.
(2)先证四边形MENF是平行四边形,再证它的一组邻边ME和MF相等.
(3)由(2)得四边形MENF是菱形,当它是正方形时,只需使∠BMC是直角,则有∠AMB+ ∠CMD=90°.又∵ ∠AMB=∠CMD,∴ △AMB和△CMD都是等腰直角三角形.
(1)证明:∵ 四边形ABCD是矩形,
∴ ∠A=∠D=90°,AB=DC.
又∵ MA=MD,
∴ △ABM≌△DCM(SAS).
(2)解:四边形MENF是菱形.
理由:∵ CF=FM,CN=NB,
∴ FN∥MB.同理可得:EN∥MC,
∴ 四边形MENF是平行四边形.
∵ △ABM≌△DCM,
∴ MB=MC.
又∵ ME=MB,MF=MC,
∴ ME=MF.
∴ 平行四边形MENF是菱形.
(3)解:2∶1.
