17.2一元二次方程的解法(5) 课件(共25张PPT)
文档属性
| 名称 | 17.2一元二次方程的解法(5) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 15:12:37 | ||
图片预览








文档简介
(共25张PPT)
沪科版八年级下册
17.2一元二次方程的解法(5)
教学目标
能灵活运用一元二次方程的四种基本解法求方程的解.
教学重点:
运用一元二次方程的四种基本解法求方程的解.
教学难点:
灵活运用一元二次方程的四种基本解法求方程的解.
复习旧知
我们学过一元二次方程的哪些解法
4.因式分解法
1.直接开平方法
2.配方法
3.公式法
解一元二次方程时,如何选择解法
复习旧知
方程没有一次项,直接开方最理想.
如果缺少常数项,因式分解没商量.
b,c相等都为零,等根是零不要忘.
b,c同时不为零,因式分解或配方.
也可直接套公式,因题而异择良方.
解一元二次方程时,如何选择解法
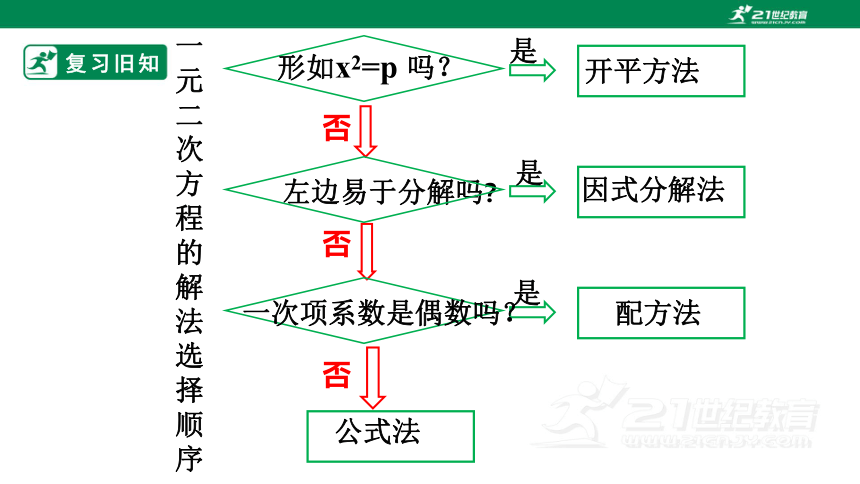
复习旧知
是
是
是
否
否
否
公式法
配方法
形如x2=p 吗?
左边易于分解吗?
一次项系数是偶数吗?
一元二次方程的解法选择顺序
因式分解法
开平方法
复习旧知
1. (2x+1)2=64 ( )
2. (x-2)2-4(x+1)2=0 ( )
3.(5x-4)2 -(4-5x)=0 ( )
4. x2-4x-10=0 ( )
5. 8x2-4x-5=0 ( )
6. x2+8x-1=0 ( )
7. 3x2 -8x-7=0 ( )
8. y2- y-1=0 ( )
选用适当方法解下列一元二次方程
因式分解法
因式分解法
开平方法
配方法
公式法
配方法
公式法
公式法
例题解析
例 解方程:
3x-2=
3x-2=7,
∴ x1=3,
或 3x-2=-7.
x2=- .
解:
根据平方根的意义,得
±7
即
(3x-2)2=49.
形如 (mx+n)2=p(p≥0)的方程用直接开平方法解.
5
3
学以致用
用直接开平方法解方程:
2x-5=
2x-3=5,
∴ x1=4,
或 2x-3=-5.
x2=-1.
解:
根据平方根的意义,得
±5
即
(1) (2x-3)2=25;
(2) (x-2)2 =3.
(1)
(2)
根据平方根的意义,得
x-2=
x-2= ,
∴ x1=2+ ,
或 x-2=- .
x2=2- .
±
即
3
3
3
3
3
例题解析
二次项系数为1,一次项系数是偶数的
一元二次方程用配方法解较为简便.
解:
移项,得
x2+6x=3
配方,得
x2 +6x+9 = 3+ 9 ;
(x+3 )2 =12
开平方,得
x+3 =
∴ x1=-3+ ,
x2= -3 - .
±
x2+6x-3=0.
例 解方程:
12
2
3
±
=
2
3
2
3
学以致用
用配方法解一元二次方程方程:
解:
移项,得
x2-4x=-1
配方,得
x2-4x+4 = -1+ 4 ;
(x-2 )2 =3
开平方,得
x-2 =
∴ x1=2+ ,
x2= 2 - .
±
x2-4x+1=0.
3
3
3
例题解析
易化成一般形式且系数的绝对值较小的
一元二次方程用公式法解.
3x2 -5x-2 =0;
∵ a=2,b= -5 ,c=-3;
∴b2-4ac=
∴x =
(-5)2 -4×3×(-2 )
=49
2×3
7
-(-5)
±
49
=
6
5
±
∴ x1=2 ,
x2=- .
1
3
解:
例 解方程:
学以致用
2x2+3x+1 =0.
∵ a=2,b= 3,c=1,
∴b2-4ac=
∴x =
32 -4×2×1
=1
2×2
1
-3
±
1
=
4
-3
±
∴ x1=- ,
x2=-1 .
解:
用公式法解一元二次方程:
1
2
例题解析
一边为0,另一边易于分解的一元二次方程,
用因式分解法解
(1) x2-9=2x(x-3);
解:
(1)
因式分解,得
(x-3)
(x
-3 -2x)=0
(x+3)(x-3)-2x(x-3)=0;
∴x-3=0,
或-x-3=0
∴ x1=3 ,
x2=-3
(2) (x-1)(x+2)=2x+4.
(2)
(x-1)(x+2)=2(x+2)
(x-1)(x+2)-2(x+2)=0
因式分解,得
(x+2) (x-1-2)=0
∴x+2=0,
或x-3=0
∴ x1=-2 ,
x2=3 .
整理,得
学以致用
用因式分解法解的一元二次方程,
(1) x (x-7)=8(7-x);
解:
(1)
因式分解,得
(x-7)
(x+8)=0
x(x-7)+8(x-7)=0;
∴x-7=0,
或x+ 8=0
∴ x1=7 ,
x2=-8
(2) (2x+1)2= - 6x-3.
(2)
(2x+1)2+3(2x+1)=0
因式分解,得
(2x+1) (2x+1+3)=0
∴2x+1=0,
或2x+4=0
∴ x2=-2.
x1=0.5 ,
整理,得
整理,得
课堂小结
2.如何根据一元二次方程的系数特点,选择适当解法
求方程的解.
1.一元二次方程有哪四种基本解法?
练习巩固
1.选用适当方法解一元二次方程,所选择合适
的方法填在横线上.
(1)解方程 x2=2√3x,用 法较合理;
(2)解方程7x2-12√7x+2=0,用 法较合理;
(3)解方程x2-2x-1999=0,用 法较合理;
(4)解方程16(x-1)2=9,用 法较合理.
直接开方
配方
公式
因式分解
练习巩固
2.对方程(1)(2x-1) =5;(2)x -x-1=0;
(3)x(x- 5)=5 -x合适的解法是( ).
A.因式分解法、公式法、因式分解法
B.直接开平方法、公式法、因式分解法
C.公式法、配方法、公式法
D.直接开平方法、配方法、公式法
B
练习巩固
3.用适当的方法解下列一元二次方程:
(1) 16(x-3)2-81=0;
(2) x2+2x-4= 0;
(3) 3x2-4x-1=0;
(4) (3x-1)(x-2)=(4x+1)(x-2).
练习巩固
(1) 16(x-3)2-81=0;
解:
16(x-3)2=81;
4(x-3)= ±9;
4(x-3)= 9,
或4(x-3)=-9;
∴ x1= ,
x2= .
21
4
3
4
练习巩固
解:
移项,得
x2+2x=4
配方,得
x2+2x+1 = 4+ 1 ;
(x+1)2 =5
开平方,得
x+1 =
∴ x1=-1+ ,
x2=-1 - .
±
5
5
5
(2) x2+2x-4= 0;
练习巩固
∵ a=3,b=-4,c=-1,
∴b2-4ac=
∴x =
(-4)2 -4×3×(-1)
=28
2×3
-(-4)
±
28
=
∴ x1= ,
x2= .
解:
(3) 3x2-4x-1=0;
4
6
±
2
7
2
3
+
7
2
3
-
7
=
2
3
±
7
练习巩固
(4) (3x-1)(x-2)=(4x+1)(x-2).
(3x-1)(x-2) -(4x+1)(x-2)=0
(x-2)[ (3x-1) -(4x+1)]=0.
(x-2)[(-x-2)=0
x-2=0
或-x-2=0
∴ x1=2 ,
x2=-2.
作业布置
今天作业
课本P31页第6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版八年级下册
17.2一元二次方程的解法(5)
教学目标
能灵活运用一元二次方程的四种基本解法求方程的解.
教学重点:
运用一元二次方程的四种基本解法求方程的解.
教学难点:
灵活运用一元二次方程的四种基本解法求方程的解.
复习旧知
我们学过一元二次方程的哪些解法
4.因式分解法
1.直接开平方法
2.配方法
3.公式法
解一元二次方程时,如何选择解法
复习旧知
方程没有一次项,直接开方最理想.
如果缺少常数项,因式分解没商量.
b,c相等都为零,等根是零不要忘.
b,c同时不为零,因式分解或配方.
也可直接套公式,因题而异择良方.
解一元二次方程时,如何选择解法
复习旧知
是
是
是
否
否
否
公式法
配方法
形如x2=p 吗?
左边易于分解吗?
一次项系数是偶数吗?
一元二次方程的解法选择顺序
因式分解法
开平方法
复习旧知
1. (2x+1)2=64 ( )
2. (x-2)2-4(x+1)2=0 ( )
3.(5x-4)2 -(4-5x)=0 ( )
4. x2-4x-10=0 ( )
5. 8x2-4x-5=0 ( )
6. x2+8x-1=0 ( )
7. 3x2 -8x-7=0 ( )
8. y2- y-1=0 ( )
选用适当方法解下列一元二次方程
因式分解法
因式分解法
开平方法
配方法
公式法
配方法
公式法
公式法
例题解析
例 解方程:
3x-2=
3x-2=7,
∴ x1=3,
或 3x-2=-7.
x2=- .
解:
根据平方根的意义,得
±7
即
(3x-2)2=49.
形如 (mx+n)2=p(p≥0)的方程用直接开平方法解.
5
3
学以致用
用直接开平方法解方程:
2x-5=
2x-3=5,
∴ x1=4,
或 2x-3=-5.
x2=-1.
解:
根据平方根的意义,得
±5
即
(1) (2x-3)2=25;
(2) (x-2)2 =3.
(1)
(2)
根据平方根的意义,得
x-2=
x-2= ,
∴ x1=2+ ,
或 x-2=- .
x2=2- .
±
即
3
3
3
3
3
例题解析
二次项系数为1,一次项系数是偶数的
一元二次方程用配方法解较为简便.
解:
移项,得
x2+6x=3
配方,得
x2 +6x+9 = 3+ 9 ;
(x+3 )2 =12
开平方,得
x+3 =
∴ x1=-3+ ,
x2= -3 - .
±
x2+6x-3=0.
例 解方程:
12
2
3
±
=
2
3
2
3
学以致用
用配方法解一元二次方程方程:
解:
移项,得
x2-4x=-1
配方,得
x2-4x+4 = -1+ 4 ;
(x-2 )2 =3
开平方,得
x-2 =
∴ x1=2+ ,
x2= 2 - .
±
x2-4x+1=0.
3
3
3
例题解析
易化成一般形式且系数的绝对值较小的
一元二次方程用公式法解.
3x2 -5x-2 =0;
∵ a=2,b= -5 ,c=-3;
∴b2-4ac=
∴x =
(-5)2 -4×3×(-2 )
=49
2×3
7
-(-5)
±
49
=
6
5
±
∴ x1=2 ,
x2=- .
1
3
解:
例 解方程:
学以致用
2x2+3x+1 =0.
∵ a=2,b= 3,c=1,
∴b2-4ac=
∴x =
32 -4×2×1
=1
2×2
1
-3
±
1
=
4
-3
±
∴ x1=- ,
x2=-1 .
解:
用公式法解一元二次方程:
1
2
例题解析
一边为0,另一边易于分解的一元二次方程,
用因式分解法解
(1) x2-9=2x(x-3);
解:
(1)
因式分解,得
(x-3)
(x
-3 -2x)=0
(x+3)(x-3)-2x(x-3)=0;
∴x-3=0,
或-x-3=0
∴ x1=3 ,
x2=-3
(2) (x-1)(x+2)=2x+4.
(2)
(x-1)(x+2)=2(x+2)
(x-1)(x+2)-2(x+2)=0
因式分解,得
(x+2) (x-1-2)=0
∴x+2=0,
或x-3=0
∴ x1=-2 ,
x2=3 .
整理,得
学以致用
用因式分解法解的一元二次方程,
(1) x (x-7)=8(7-x);
解:
(1)
因式分解,得
(x-7)
(x+8)=0
x(x-7)+8(x-7)=0;
∴x-7=0,
或x+ 8=0
∴ x1=7 ,
x2=-8
(2) (2x+1)2= - 6x-3.
(2)
(2x+1)2+3(2x+1)=0
因式分解,得
(2x+1) (2x+1+3)=0
∴2x+1=0,
或2x+4=0
∴ x2=-2.
x1=0.5 ,
整理,得
整理,得
课堂小结
2.如何根据一元二次方程的系数特点,选择适当解法
求方程的解.
1.一元二次方程有哪四种基本解法?
练习巩固
1.选用适当方法解一元二次方程,所选择合适
的方法填在横线上.
(1)解方程 x2=2√3x,用 法较合理;
(2)解方程7x2-12√7x+2=0,用 法较合理;
(3)解方程x2-2x-1999=0,用 法较合理;
(4)解方程16(x-1)2=9,用 法较合理.
直接开方
配方
公式
因式分解
练习巩固
2.对方程(1)(2x-1) =5;(2)x -x-1=0;
(3)x(x- 5)=5 -x合适的解法是( ).
A.因式分解法、公式法、因式分解法
B.直接开平方法、公式法、因式分解法
C.公式法、配方法、公式法
D.直接开平方法、配方法、公式法
B
练习巩固
3.用适当的方法解下列一元二次方程:
(1) 16(x-3)2-81=0;
(2) x2+2x-4= 0;
(3) 3x2-4x-1=0;
(4) (3x-1)(x-2)=(4x+1)(x-2).
练习巩固
(1) 16(x-3)2-81=0;
解:
16(x-3)2=81;
4(x-3)= ±9;
4(x-3)= 9,
或4(x-3)=-9;
∴ x1= ,
x2= .
21
4
3
4
练习巩固
解:
移项,得
x2+2x=4
配方,得
x2+2x+1 = 4+ 1 ;
(x+1)2 =5
开平方,得
x+1 =
∴ x1=-1+ ,
x2=-1 - .
±
5
5
5
(2) x2+2x-4= 0;
练习巩固
∵ a=3,b=-4,c=-1,
∴b2-4ac=
∴x =
(-4)2 -4×3×(-1)
=28
2×3
-(-4)
±
28
=
∴ x1= ,
x2= .
解:
(3) 3x2-4x-1=0;
4
6
±
2
7
2
3
+
7
2
3
-
7
=
2
3
±
7
练习巩固
(4) (3x-1)(x-2)=(4x+1)(x-2).
(3x-1)(x-2) -(4x+1)(x-2)=0
(x-2)[ (3x-1) -(4x+1)]=0.
(x-2)[(-x-2)=0
x-2=0
或-x-2=0
∴ x1=2 ,
x2=-2.
作业布置
今天作业
课本P31页第6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
