17.5一元二次方程的应用(1) 课件(共25张PPT)
文档属性
| 名称 | 17.5一元二次方程的应用(1) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 15:32:24 | ||
图片预览




文档简介
(共25张PPT)
17.5一元二次方程的应用(1)
沪科版八年级下册
教学目标
1.能正确利用面积公式列出关于面积的一元二次方程;
2.进一步深入体会一元二次方程在实际生活中的应用,
经历将实际问题转化为数学问题的过程,提高数学
应用意识.
教学重点:
利用面积间的和差关系建立一元二次方程模型,解决实际题.
教学难点: 问题中隐藏的等量关系.
新知导入
列方程解应用题的一般步骤是什么?
第一步:审题,明确已知和未知;
第二步:找相等关系;
第三步:设元,列方程,并解方程;
第五步:作答.
第四步:检验根的合理性;
新知讲解
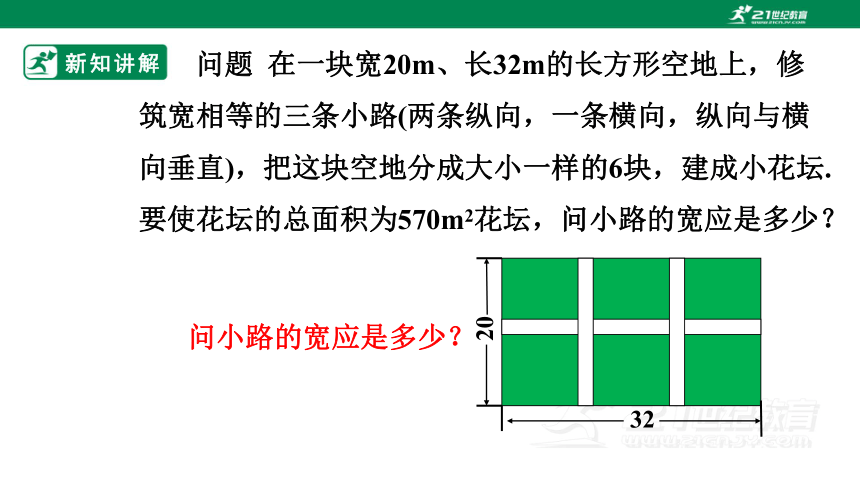
问题 在一块宽20m、长32m的长方形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把这块空地分成大小一样的6块,建成小花坛.要使花坛的总面积为570m2花坛,问小路的宽应是多少?
32
20
问小路的宽应是多少?
新知讲解
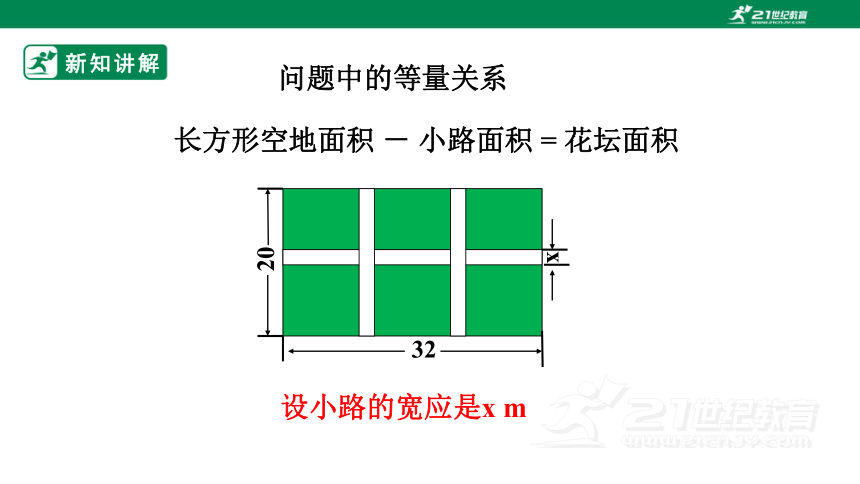
长方形空地面积 - 小路面积 = 花坛面积
32
20
x
问题中的等量关系
设小路的宽应是x m
新知讲解
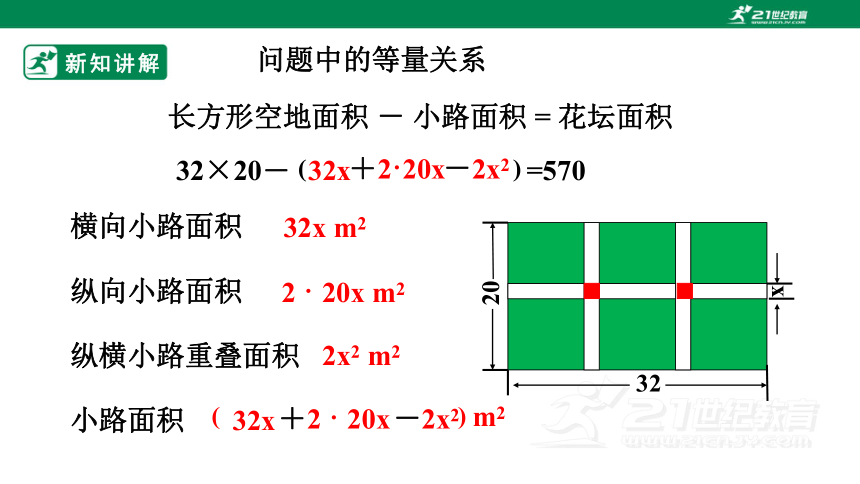
长方形空地面积 - 小路面积 = 花坛面积
问题中的等量关系
32×20
=570
横向小路面积
32x m2
纵向小路面积
2 · 20x m2
纵横小路重叠面积
2x2 m2
小路面积
-
( )
32x
+2·20x
-2x2
( )
m2
32x
+2 · 20x
-2x2
32
20
x
新知讲解
去括号,得
640-32x-40x+2x2=570;
移项,得
合并同类项,得
2x2 -72x+ 70=0.
640-32x-40x+2x2-570=0;
x2 -36x+35=0.
长方形空地面积 - 小路面积 = 花坛面积
32×20
=570
-
( )
32x
+2·20x
-2x2
(x-1)
(x-35)
=0
或 x-35=0
∴x-1=0
∴ x1= 1 ,
x2=35 .
32
20
x
新知讲解
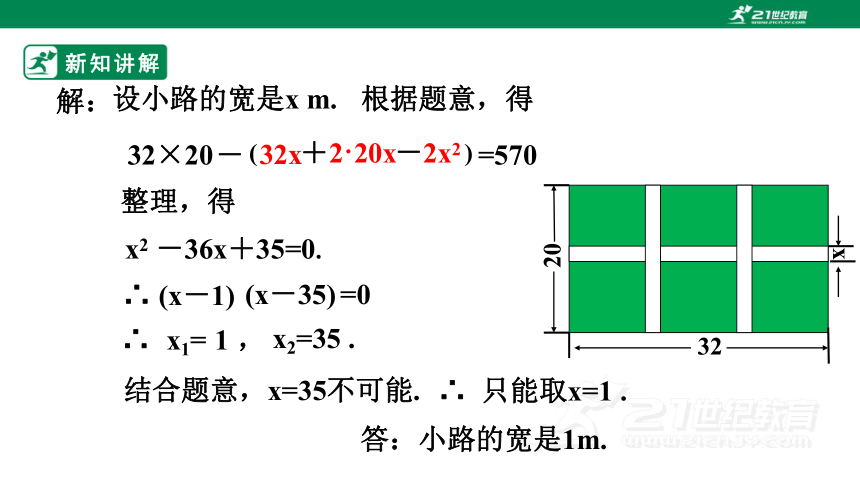
根据题意,得
整理,得
x2 -36x+35=0.
解:
32×20
=570
( )
32x
+2·20x
-2x2
∴ (x-1)
(x-35) =0
∴ x1= 1 ,
x2=35 .
设小路的宽是x m.
结合题意,x=35不可能.
∴ 只能取x=1 .
答:小路的宽是1m.
32
20
x
-
方法总结
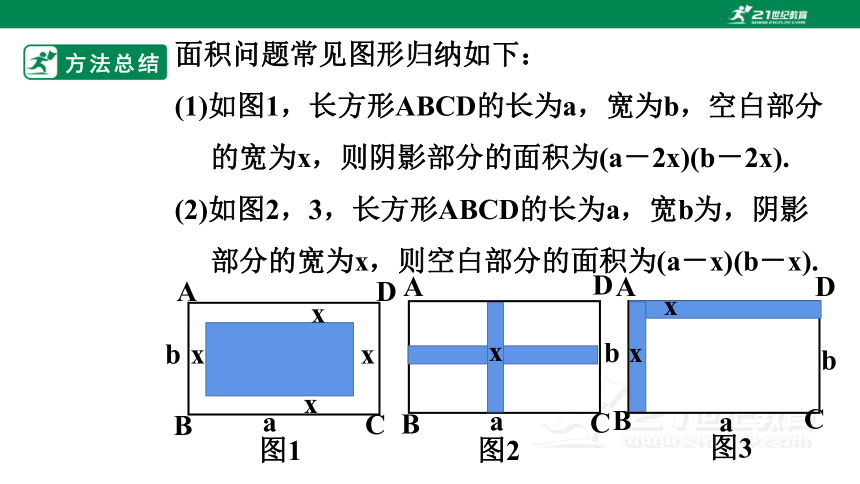
面积问题常见图形归纳如下:
(1)如图1,长方形ABCD的长为a,宽为b,空白部分
的宽为x,则阴影部分的面积为(a-2x)(b-2x).
(2)如图2,3,长方形ABCD的长为a,宽b为,阴影
部分的宽为x,则空白部分的面积为(a-x)(b-x).
A
B
C
D
a
图2
A
B
C
D
a
b
x
图1
b
x
x
x
x
图3
A
B
C
D
a
b
x
x
例题解析
(课本第42页例4 )正方形金属片一块,将其四个角各截去一个相同大小的小正方形,围成高20cm,容积为2 880cm3的开口方盒,问原金属片边长是多少?
x
20
20
已知:
方盒的高
方盒的容积
未知:
20cm
2880cm3
原金属片的边长
小正方形的边长
20cm
例题解析
x
20
20
问题中的等量关系
方盒的容积
方盒的底面积
×高
=2880
=2880
方盒的高
=20
方盒的底面是什么形状?
盒底面积=
( 正方形 )
(课本第42页例4 )正方形金属片一块,将其四个角各截去一个相同大小的小正方形,围成高20cm,容积为2 880cm3的开口方盒,问原金属片边长是多少?
盒底边长的平方
例题解析
x
20
20
问题中的等量关系
方盒的容积
方盒的底面积
×高
=2880
=2880
方盒的高
=20
盒底面积=
方盒的底面边长是多少?
方盒的底面边长与金属片的边长有什么关系
盒底边长=
金属片的边长
- 2小正方形的边长
x-40
(x-40)2
=2880
·20
盒底边长的平方
例题解析
设原金属片边长为xcm,
x
20
20
x-40
解:
根据题意,得
则方盒的底边长为
(x-40)cm.
(x-40)2
=2 880.
×高
=2880
盒底边长的平方
20·
(x-40)2
=144.
x-40
=±12
x1=52,
x2=28.
x2=28 < 40,不合题意,舍去.
∴x=52.
答:原金属片边长52cm.
例题解析
x
20
20
x-40
问题中的等量关系
方盒的容积
方盒的底面积
×高
=2880
=2880
方盒的高
=20
方盒的底面边长的平方
方盒的底面积=
盒底边长=
金属片的边长
- 2小正方形的边长
明显的
隐藏的
课堂练习
一长方形铁片长40m,宽30m,在它的四周截去一个全等的小正方形,然后折成一个无盖的长方体盒子,并使底面积所占面积为原来长方形形面积的一半.
40m
30m
xm
xm
问题中的等量关系
底面长方形面积=原来长方形形面积的一半.
底面长方形的长=原长方形的长
-2小正方形的边长
底面长方形的宽=原长方形的宽
-2小正方形的边长
底面长×
底面宽
= × 40×30
1
2
课堂练习
40m
30m
xm
xm
小正方形的边长为xm,
解:
根据题意,得
(40-2x)
(30-2x)
= × 40×30
1200-80x
-60x+4x2
= 600
4x2-140x+600=0
x2-35x+150=0
(x-5)
(x-30)=0
x1=5,
x2=30.
(舍去)
1
2
答:小正方形的边长为5m.
课堂小结
面积问题
(1)规则图形:套用面积公式列方程.
(2)不规则图形:通过割补变为规则图形后,
利用面积间的和差关系列方程.
利用面积间的和差关系建立一元二次方程模型解决实际题时,要注意哪些方法?
1.扬帆中学有一块长 30 m,宽20m的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为xm,则可列方程为( ) .
A.(30-x)(20-x)= ×20×30
B. 30x+2×20x= ×20×30
C. (30-x)(20-x)= ×20×30
D. (30-2x)(20-x)= ×20×30
练习巩固
3
4
1
4
1
4
3
4
D
30m
20m
xm
xm
练习巩固
2.如图,长方形ABCD的周长为20m,以AB、AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和正方形ADGH的面积之和为68m2.则长方形ABCD的面积为( ).
A
B
C
D
E
F
G
H
A.24m2 B.21m2
C.16m2 D.9m2
C
练习巩固
3.如图,小明用一张长11cm,宽7cm的矩形纸板制作一个底面积积为 21 cm 的无盖长方体纸盒,他将纸板 的四个角各剪去一个同样大小的正方形, 将四周向上折叠即可(损耗不计).设剪去的的正方形边长为xcm,则可列出关于的方程为 .
(11-2x)(7-2x)=21
11cm
7cm
xcm
xcm
练习巩固
4.如图,在一块长10m、宽8m的长方形空地上,修筑宽相等的小路(图中阴影部分),余下部分种草.要使草坪的面积为48m2,则小路的宽应是 m .
2
练习巩固
解:设BC边的长为x米,根据题意,得
x· =120,
解得 x1=12,x2=20.
∵20>16,
答:该矩形草坪BC边的长为12米.
∴x2=20不合题意,舍去.
32-x
2
5.如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的长方形草坪ABCD.求该长方形草坪BC边的长.
∴x=12.
作业布置
今天作业
课本P47页第1题
课本P48页第7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
17.5一元二次方程的应用(1)
沪科版八年级下册
教学目标
1.能正确利用面积公式列出关于面积的一元二次方程;
2.进一步深入体会一元二次方程在实际生活中的应用,
经历将实际问题转化为数学问题的过程,提高数学
应用意识.
教学重点:
利用面积间的和差关系建立一元二次方程模型,解决实际题.
教学难点: 问题中隐藏的等量关系.
新知导入
列方程解应用题的一般步骤是什么?
第一步:审题,明确已知和未知;
第二步:找相等关系;
第三步:设元,列方程,并解方程;
第五步:作答.
第四步:检验根的合理性;
新知讲解
问题 在一块宽20m、长32m的长方形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把这块空地分成大小一样的6块,建成小花坛.要使花坛的总面积为570m2花坛,问小路的宽应是多少?
32
20
问小路的宽应是多少?
新知讲解
长方形空地面积 - 小路面积 = 花坛面积
32
20
x
问题中的等量关系
设小路的宽应是x m
新知讲解
长方形空地面积 - 小路面积 = 花坛面积
问题中的等量关系
32×20
=570
横向小路面积
32x m2
纵向小路面积
2 · 20x m2
纵横小路重叠面积
2x2 m2
小路面积
-
( )
32x
+2·20x
-2x2
( )
m2
32x
+2 · 20x
-2x2
32
20
x
新知讲解
去括号,得
640-32x-40x+2x2=570;
移项,得
合并同类项,得
2x2 -72x+ 70=0.
640-32x-40x+2x2-570=0;
x2 -36x+35=0.
长方形空地面积 - 小路面积 = 花坛面积
32×20
=570
-
( )
32x
+2·20x
-2x2
(x-1)
(x-35)
=0
或 x-35=0
∴x-1=0
∴ x1= 1 ,
x2=35 .
32
20
x
新知讲解
根据题意,得
整理,得
x2 -36x+35=0.
解:
32×20
=570
( )
32x
+2·20x
-2x2
∴ (x-1)
(x-35) =0
∴ x1= 1 ,
x2=35 .
设小路的宽是x m.
结合题意,x=35不可能.
∴ 只能取x=1 .
答:小路的宽是1m.
32
20
x
-
方法总结
面积问题常见图形归纳如下:
(1)如图1,长方形ABCD的长为a,宽为b,空白部分
的宽为x,则阴影部分的面积为(a-2x)(b-2x).
(2)如图2,3,长方形ABCD的长为a,宽b为,阴影
部分的宽为x,则空白部分的面积为(a-x)(b-x).
A
B
C
D
a
图2
A
B
C
D
a
b
x
图1
b
x
x
x
x
图3
A
B
C
D
a
b
x
x
例题解析
(课本第42页例4 )正方形金属片一块,将其四个角各截去一个相同大小的小正方形,围成高20cm,容积为2 880cm3的开口方盒,问原金属片边长是多少?
x
20
20
已知:
方盒的高
方盒的容积
未知:
20cm
2880cm3
原金属片的边长
小正方形的边长
20cm
例题解析
x
20
20
问题中的等量关系
方盒的容积
方盒的底面积
×高
=2880
=2880
方盒的高
=20
方盒的底面是什么形状?
盒底面积=
( 正方形 )
(课本第42页例4 )正方形金属片一块,将其四个角各截去一个相同大小的小正方形,围成高20cm,容积为2 880cm3的开口方盒,问原金属片边长是多少?
盒底边长的平方
例题解析
x
20
20
问题中的等量关系
方盒的容积
方盒的底面积
×高
=2880
=2880
方盒的高
=20
盒底面积=
方盒的底面边长是多少?
方盒的底面边长与金属片的边长有什么关系
盒底边长=
金属片的边长
- 2小正方形的边长
x-40
(x-40)2
=2880
·20
盒底边长的平方
例题解析
设原金属片边长为xcm,
x
20
20
x-40
解:
根据题意,得
则方盒的底边长为
(x-40)cm.
(x-40)2
=2 880.
×高
=2880
盒底边长的平方
20·
(x-40)2
=144.
x-40
=±12
x1=52,
x2=28.
x2=28 < 40,不合题意,舍去.
∴x=52.
答:原金属片边长52cm.
例题解析
x
20
20
x-40
问题中的等量关系
方盒的容积
方盒的底面积
×高
=2880
=2880
方盒的高
=20
方盒的底面边长的平方
方盒的底面积=
盒底边长=
金属片的边长
- 2小正方形的边长
明显的
隐藏的
课堂练习
一长方形铁片长40m,宽30m,在它的四周截去一个全等的小正方形,然后折成一个无盖的长方体盒子,并使底面积所占面积为原来长方形形面积的一半.
40m
30m
xm
xm
问题中的等量关系
底面长方形面积=原来长方形形面积的一半.
底面长方形的长=原长方形的长
-2小正方形的边长
底面长方形的宽=原长方形的宽
-2小正方形的边长
底面长×
底面宽
= × 40×30
1
2
课堂练习
40m
30m
xm
xm
小正方形的边长为xm,
解:
根据题意,得
(40-2x)
(30-2x)
= × 40×30
1200-80x
-60x+4x2
= 600
4x2-140x+600=0
x2-35x+150=0
(x-5)
(x-30)=0
x1=5,
x2=30.
(舍去)
1
2
答:小正方形的边长为5m.
课堂小结
面积问题
(1)规则图形:套用面积公式列方程.
(2)不规则图形:通过割补变为规则图形后,
利用面积间的和差关系列方程.
利用面积间的和差关系建立一元二次方程模型解决实际题时,要注意哪些方法?
1.扬帆中学有一块长 30 m,宽20m的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为xm,则可列方程为( ) .
A.(30-x)(20-x)= ×20×30
B. 30x+2×20x= ×20×30
C. (30-x)(20-x)= ×20×30
D. (30-2x)(20-x)= ×20×30
练习巩固
3
4
1
4
1
4
3
4
D
30m
20m
xm
xm
练习巩固
2.如图,长方形ABCD的周长为20m,以AB、AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和正方形ADGH的面积之和为68m2.则长方形ABCD的面积为( ).
A
B
C
D
E
F
G
H
A.24m2 B.21m2
C.16m2 D.9m2
C
练习巩固
3.如图,小明用一张长11cm,宽7cm的矩形纸板制作一个底面积积为 21 cm 的无盖长方体纸盒,他将纸板 的四个角各剪去一个同样大小的正方形, 将四周向上折叠即可(损耗不计).设剪去的的正方形边长为xcm,则可列出关于的方程为 .
(11-2x)(7-2x)=21
11cm
7cm
xcm
xcm
练习巩固
4.如图,在一块长10m、宽8m的长方形空地上,修筑宽相等的小路(图中阴影部分),余下部分种草.要使草坪的面积为48m2,则小路的宽应是 m .
2
练习巩固
解:设BC边的长为x米,根据题意,得
x· =120,
解得 x1=12,x2=20.
∵20>16,
答:该矩形草坪BC边的长为12米.
∴x2=20不合题意,舍去.
32-x
2
5.如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的长方形草坪ABCD.求该长方形草坪BC边的长.
∴x=12.
作业布置
今天作业
课本P47页第1题
课本P48页第7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
