17.5一元二次方程的应用(5) 课件(共25张PPT)
文档属性
| 名称 | 17.5一元二次方程的应用(5) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 15:41:39 | ||
图片预览








文档简介
(共25张PPT)
沪科版八年级下册
17.5一元二次方程的应用(5)
教学目标
1.使学生掌握运用去分母或换元的方法解可化为
一元二次方程的分式方程;使学生理解转化的
数学基本思想.
2.使学生能够利用最简分母进行验根.
教学重点
掌握可化为一元二次方程的分式方程的解法.
教学难点
使学生认识解分式方程必须检验的道理,且方程 的解符合实际问题的要求.
复习旧知
怎样解分式方程 怎样进行检验
解:方程两边同乘(x+2)(x-2)得,
x-2+4x-2(x+2)=x2-4
整理,得x2-3x+2=0
当x=1时,(x+2)(x-2) ≠0,
当x=2时,(x+2)(x-2)=0,
∴x=2不是原方程的解,原方程解为x=1.
解得 x=1,x=2,
1
x+2
+
+
=1
2
2-x
4x
x2-4
检验:
新知导入
把分式方程 去分母,并整理为一元二次方程的一般形式,得 .
答:分式方程两边同乘以最简公分母,将分式方程转化为一元二次方程(整式方程),解一元二次方程,并检验所求得的根是否为分式方程的根.
如何解可化为一元二次方程的分式方程
4
x
-
=1
1
x-1
x2-4x+4=0
例题解析
例5 一组学生组织春游,预计共需费用120元.后来又有2人参加进来,费用不变,这样每人可少分摊3元.问原来这组学生的人数是多少?
问题中的等量关系
原来这组学生数×每人分摊的费用=120
原来每人分摊的费用-加人后每人分摊的费用=3
后来这组学生数×加人后每人分摊的费用=120
例题解析
设原来这组学生的人数是x人,则把题中信息整理成下表:
例5 一组学生组织春游,预计共需费用120元.后来又有2人参加进来,费用不变,这样每人可少分摊3元.问原来这组学生的人数是多少?
分析:
总费用/元 人数/人 每人费用/元
原来 120 x
后来 120 x+2
120/x
120/(x+2)
新知导入
x1=8,
x2= -10.
经检验, x1=8, x2=-10 都是原方程的根,
但x2= - 10不符合题意,应舍去.
解:
设原来这组学生的人数是x人,
x2 + 2x - 80= 0
根据题意,得
(x-8)
(x+10)=0
120(x+2)
-120x
= 3x
(x+2)
120x+240
-120x
= 3x2+6x
3x2+6x-240=0
120
x
-
120
x+2
=3
例题解析
整理, 得
∴ x1=8,
x2= -10.
经检验, x1=8, x2=-10 都是原方程的根.
但x2= –10不符合题意,应舍去.
答:原来这组学生的人数是8人.
解:
设原来这组学生的人数是x人,
x2 + 2x - 80= 0
根据题意,得
120
x
-
120
x+2
=3
∴(x-8)
(x+10)=0
检验
一检是否是原分式方程的解
二检原分式方程的解是否使实际问题有意义
例题解析
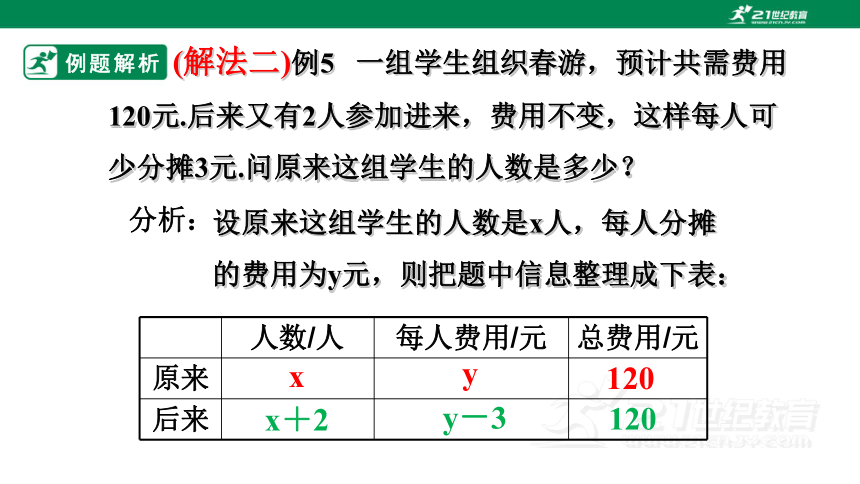
设原来这组学生的人数是x人,每人分摊的费用为y元,则把题中信息整理成下表:
每人费用/元 总费用/元
原来
后来
(解法二)例5 一组学生组织春游,预计共需费用120元.后来又有2人参加进来,费用不变,这样每人可少分摊3元.问原来这组学生的人数是多少?
分析:
人数/人
x
y
x+2
y-3
120
120
例题解析
解:
设原来这组学生的人数是x人,
则有
每人分摊的费用为y元,
xy
(x+2)
(y-3)
=120
=120
①
②
③
④
由②得
xy-3x
+2y-6
=120
2y= 3x+6
由①得
x · 2y =240
把③代入④得
x · (3x+6)=240
x1=8,
x2= -10
x2 + 2x-80= 0;
(x-8)
(x+10)=0.
(舍去) .
例题解析
解:
设原来这组学生的人数是x人,
则有
每人分摊的费用为y元,
xy
(x+2)
(y-3)
=120
=120
①
②
解这个方程组, 得
x=8
y=15
x=-10
y=-12
(舍去)
答:
原来这组学生的人数是8人.
方法总结
解法1的优点是方程比较容易解,
解法2的优点是不需检验,
但必须
注意检验,
且要双检验.
并且适合有两问
缺点是解方程组的过程稍麻烦.
的题目,
课堂练习
1.小王乘公共汽车从甲地到相距 40 km 的乙地办事,然后乘出租车返回,出租车的平均速度比公共汽车 快 20 km/h,回来路上花的时间比去时节省了 . 设公共汽车的平均速度是xkm/h,则下面所列方程正确的是 ( ) .
A. B.
C. D.
A
4
1
40
x+20
=
4
3
×
x
40
40
x+20
=
x
40
4
3
×
40
x+20
=
4
1
+
x
40
x
40
40
x+20
=
4
1
-
课堂练习
2.今年我市工业试验区投资 50 760 万元开发了多个项目,今后还将投资 106 960 万元开发多个新项目, 每个新项目平均投资比今年每个项目平均投资多 500万元,并且新增项目数量比今年多 20 个.假设 今年每个项目平均投资是x万元,那么下列方程符 合题意的是 ( ) .
A. B.
C. D.
B
-
=20
50760
x
106960
x+500
-
=500
50760
x
106960
x+20
-
=500
50760
x
106960
x+20
-
=20
50760
x
106960
x+500
课堂练习
3.甲,乙两组工人合做某项工作,10 天后,因乙组另有任务,甲组再单独做2天才完成任务.如果单独完 成这项工作,甲组比乙组快4天,设乙组单独完成要工天,则可列方程为 .
10
x
+
=1
12
x-4
课堂小结
1.解可化为一元二次方程的分式方程怎样验根?
2.列可化为一元二次方程的分式方程解应用题
要怎样验根?
检验要2检
一检未知数的值是否是原分式方程的解;
二检原分式方程的解是否使实际问题有意义.
练习巩固
1.解分式方程:
去分母,得
整理,得
6x+5(x+1)=(x+4)(x-1)
x2-8x-9=0
∴(x+1)(x-9)=0,
+
=
5
x-1
6x
x2-1
x+4
x+1
检验:
∴原方程的根是x=9.
∴x=-1,或x=9.
x=9是原方程的根.
x= -1是增根;
当x=-1时,(x+1)(x-1)=0,
当x=9时,(x+1)(x-1) ≠0,
练习巩固
2.某商店以2400元购进某种盒装茶叶,第一个月每盒按进价增加 20%作为售价,售出50盒,第二个月每盒以低于进价5元作为售价,售完余下的茶叶.在整个买卖过程中赢利 350 元,则每盒茶叶的进价为 ( ).
A.40元 B.50元 C.60元 D.70 元
A
50·(1+20%)x
+
(x-5)
( -50)
-2400=350
2400
x
设每盒茶叶的进价为x元
练习巩固
3.杭州市到北京的铁路长1487 km.火车的原平均速度为 xkm/h,提速后平均速度增加了 70 km/h,由杭州到北京的行驶时间缩短了3h,则可列方程为
.
-
=3
1487
x
1487
x+70
练习巩固
4.甲、乙两班学生绿化校园,如果两班合作6天可以完成,如果单独工作,甲班比乙班少用5天,那么甲、乙两班单独工作分别需要 .
10 天和15天
设甲班单独工作需要x天,
则乙班单独工作需要(x+5)天.
6
x
+
=1
6
x+5
练习巩固
5.甲、乙两地间铁路长2 400km,经技术改造后,列车实 现了提速,提速后比提速前增加 20 km/h,列车从甲地到乙地行驶时间减少4h.已知列车在现有条件下完全行驶的速度不超过140km/h.请你用学过的数学知识说明这条铁路在现有条件下是否还可以再次提速
练习巩固
解:设提速后列车速度为xkm/h,则提速前的速度为
-
=4
2400
x
2400
x-20
∴x1=120,x2=-100.
经检验, x1=120, x2=-100 都是原方程的根.
但x2= –100不符合题意,应舍去.
∴x=120.
∵120km/h<140/kh,
(x-20) km/h,
根据题意,得
∴可以再次提速.
作业布置
今天作业
课本P47页第4题
课本P45页第5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版八年级下册
17.5一元二次方程的应用(5)
教学目标
1.使学生掌握运用去分母或换元的方法解可化为
一元二次方程的分式方程;使学生理解转化的
数学基本思想.
2.使学生能够利用最简分母进行验根.
教学重点
掌握可化为一元二次方程的分式方程的解法.
教学难点
使学生认识解分式方程必须检验的道理,且方程 的解符合实际问题的要求.
复习旧知
怎样解分式方程 怎样进行检验
解:方程两边同乘(x+2)(x-2)得,
x-2+4x-2(x+2)=x2-4
整理,得x2-3x+2=0
当x=1时,(x+2)(x-2) ≠0,
当x=2时,(x+2)(x-2)=0,
∴x=2不是原方程的解,原方程解为x=1.
解得 x=1,x=2,
1
x+2
+
+
=1
2
2-x
4x
x2-4
检验:
新知导入
把分式方程 去分母,并整理为一元二次方程的一般形式,得 .
答:分式方程两边同乘以最简公分母,将分式方程转化为一元二次方程(整式方程),解一元二次方程,并检验所求得的根是否为分式方程的根.
如何解可化为一元二次方程的分式方程
4
x
-
=1
1
x-1
x2-4x+4=0
例题解析
例5 一组学生组织春游,预计共需费用120元.后来又有2人参加进来,费用不变,这样每人可少分摊3元.问原来这组学生的人数是多少?
问题中的等量关系
原来这组学生数×每人分摊的费用=120
原来每人分摊的费用-加人后每人分摊的费用=3
后来这组学生数×加人后每人分摊的费用=120
例题解析
设原来这组学生的人数是x人,则把题中信息整理成下表:
例5 一组学生组织春游,预计共需费用120元.后来又有2人参加进来,费用不变,这样每人可少分摊3元.问原来这组学生的人数是多少?
分析:
总费用/元 人数/人 每人费用/元
原来 120 x
后来 120 x+2
120/x
120/(x+2)
新知导入
x1=8,
x2= -10.
经检验, x1=8, x2=-10 都是原方程的根,
但x2= - 10不符合题意,应舍去.
解:
设原来这组学生的人数是x人,
x2 + 2x - 80= 0
根据题意,得
(x-8)
(x+10)=0
120(x+2)
-120x
= 3x
(x+2)
120x+240
-120x
= 3x2+6x
3x2+6x-240=0
120
x
-
120
x+2
=3
例题解析
整理, 得
∴ x1=8,
x2= -10.
经检验, x1=8, x2=-10 都是原方程的根.
但x2= –10不符合题意,应舍去.
答:原来这组学生的人数是8人.
解:
设原来这组学生的人数是x人,
x2 + 2x - 80= 0
根据题意,得
120
x
-
120
x+2
=3
∴(x-8)
(x+10)=0
检验
一检是否是原分式方程的解
二检原分式方程的解是否使实际问题有意义
例题解析
设原来这组学生的人数是x人,每人分摊的费用为y元,则把题中信息整理成下表:
每人费用/元 总费用/元
原来
后来
(解法二)例5 一组学生组织春游,预计共需费用120元.后来又有2人参加进来,费用不变,这样每人可少分摊3元.问原来这组学生的人数是多少?
分析:
人数/人
x
y
x+2
y-3
120
120
例题解析
解:
设原来这组学生的人数是x人,
则有
每人分摊的费用为y元,
xy
(x+2)
(y-3)
=120
=120
①
②
③
④
由②得
xy-3x
+2y-6
=120
2y= 3x+6
由①得
x · 2y =240
把③代入④得
x · (3x+6)=240
x1=8,
x2= -10
x2 + 2x-80= 0;
(x-8)
(x+10)=0.
(舍去) .
例题解析
解:
设原来这组学生的人数是x人,
则有
每人分摊的费用为y元,
xy
(x+2)
(y-3)
=120
=120
①
②
解这个方程组, 得
x=8
y=15
x=-10
y=-12
(舍去)
答:
原来这组学生的人数是8人.
方法总结
解法1的优点是方程比较容易解,
解法2的优点是不需检验,
但必须
注意检验,
且要双检验.
并且适合有两问
缺点是解方程组的过程稍麻烦.
的题目,
课堂练习
1.小王乘公共汽车从甲地到相距 40 km 的乙地办事,然后乘出租车返回,出租车的平均速度比公共汽车 快 20 km/h,回来路上花的时间比去时节省了 . 设公共汽车的平均速度是xkm/h,则下面所列方程正确的是 ( ) .
A. B.
C. D.
A
4
1
40
x+20
=
4
3
×
x
40
40
x+20
=
x
40
4
3
×
40
x+20
=
4
1
+
x
40
x
40
40
x+20
=
4
1
-
课堂练习
2.今年我市工业试验区投资 50 760 万元开发了多个项目,今后还将投资 106 960 万元开发多个新项目, 每个新项目平均投资比今年每个项目平均投资多 500万元,并且新增项目数量比今年多 20 个.假设 今年每个项目平均投资是x万元,那么下列方程符 合题意的是 ( ) .
A. B.
C. D.
B
-
=20
50760
x
106960
x+500
-
=500
50760
x
106960
x+20
-
=500
50760
x
106960
x+20
-
=20
50760
x
106960
x+500
课堂练习
3.甲,乙两组工人合做某项工作,10 天后,因乙组另有任务,甲组再单独做2天才完成任务.如果单独完 成这项工作,甲组比乙组快4天,设乙组单独完成要工天,则可列方程为 .
10
x
+
=1
12
x-4
课堂小结
1.解可化为一元二次方程的分式方程怎样验根?
2.列可化为一元二次方程的分式方程解应用题
要怎样验根?
检验要2检
一检未知数的值是否是原分式方程的解;
二检原分式方程的解是否使实际问题有意义.
练习巩固
1.解分式方程:
去分母,得
整理,得
6x+5(x+1)=(x+4)(x-1)
x2-8x-9=0
∴(x+1)(x-9)=0,
+
=
5
x-1
6x
x2-1
x+4
x+1
检验:
∴原方程的根是x=9.
∴x=-1,或x=9.
x=9是原方程的根.
x= -1是增根;
当x=-1时,(x+1)(x-1)=0,
当x=9时,(x+1)(x-1) ≠0,
练习巩固
2.某商店以2400元购进某种盒装茶叶,第一个月每盒按进价增加 20%作为售价,售出50盒,第二个月每盒以低于进价5元作为售价,售完余下的茶叶.在整个买卖过程中赢利 350 元,则每盒茶叶的进价为 ( ).
A.40元 B.50元 C.60元 D.70 元
A
50·(1+20%)x
+
(x-5)
( -50)
-2400=350
2400
x
设每盒茶叶的进价为x元
练习巩固
3.杭州市到北京的铁路长1487 km.火车的原平均速度为 xkm/h,提速后平均速度增加了 70 km/h,由杭州到北京的行驶时间缩短了3h,则可列方程为
.
-
=3
1487
x
1487
x+70
练习巩固
4.甲、乙两班学生绿化校园,如果两班合作6天可以完成,如果单独工作,甲班比乙班少用5天,那么甲、乙两班单独工作分别需要 .
10 天和15天
设甲班单独工作需要x天,
则乙班单独工作需要(x+5)天.
6
x
+
=1
6
x+5
练习巩固
5.甲、乙两地间铁路长2 400km,经技术改造后,列车实 现了提速,提速后比提速前增加 20 km/h,列车从甲地到乙地行驶时间减少4h.已知列车在现有条件下完全行驶的速度不超过140km/h.请你用学过的数学知识说明这条铁路在现有条件下是否还可以再次提速
练习巩固
解:设提速后列车速度为xkm/h,则提速前的速度为
-
=4
2400
x
2400
x-20
∴x1=120,x2=-100.
经检验, x1=120, x2=-100 都是原方程的根.
但x2= –100不符合题意,应舍去.
∴x=120.
∵120km/h<140/kh,
(x-20) km/h,
根据题意,得
∴可以再次提速.
作业布置
今天作业
课本P47页第4题
课本P45页第5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
