3.2.1双曲线及其标准方程 课件(共22张PPT)
文档属性
| 名称 | 3.2.1双曲线及其标准方程 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 323.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 11:09:23 | ||
图片预览







文档简介
(共22张PPT)
双曲线及其标准方程
Standard equation
Hyperbola
一、类比探究
思 考
我们知道
与两个定点距离的和为非零常数(大于两个定点间的距离)的点的轨迹是椭圆。
那么,与两个定点距离的差为非零常数的点的轨迹是什么?
点的轨迹(椭圆):
与两个定点距离的和为非零常数
点的轨迹(双曲线一支):
与两个定点距离的差为非零常数
二、新知探究
1、双曲线的定义:
我们把平面内与两个定点F1、F2的距离的差的绝对值等于常数(小于| F1F2 |) 的点的轨迹叫做双曲线, 这两个定点叫做双曲线的焦点, 两焦点间的距离叫做双曲线的焦距.
2、双曲线的标准方程:
思 考
x
y
我们应该建立怎样的平面直角坐标系来方面求出双曲线的标准方程?
x
y
设P(x, y)是双曲线上任意一点,双曲线的焦距为2c(c>0),那么,焦点F1, F2的坐标分别是(-c, 0), (c, 0),又设点P与F1, F2的距离的差的绝对值等于常数2a.
2、双曲线的标准方程:
思 考
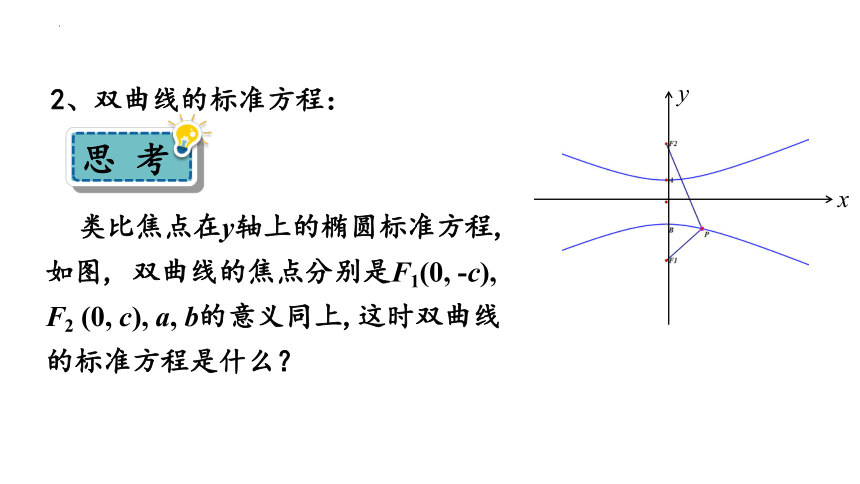
2、双曲线的标准方程:
类比焦点在y轴上的椭圆标准方程,如图, 双曲线的焦点分别是F1(0, -c), F2 (0, c), a, b的意义同上,这时双曲线的标准方程是什么?
x
y
思 考
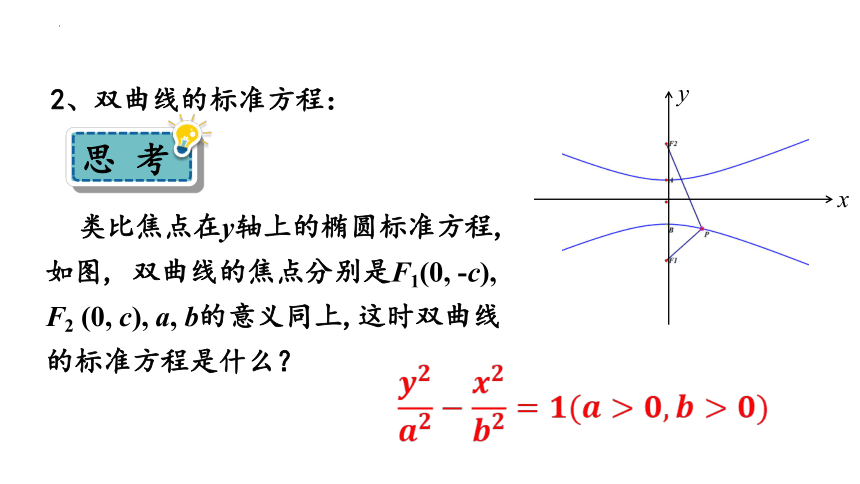
2、双曲线的标准方程:
类比焦点在y轴上的椭圆标准方程,如图, 双曲线的焦点分别是F1(0, -c), F2 (0, c), a, b的意义同上,这时双曲线的标准方程是什么?
x
y
3、椭圆方程与双曲线方程之间的区别:
椭圆 双曲线
定义
方程
焦点
a,b,c关系
3、椭圆方程与双曲线方程之间的区别:
椭圆 双曲线
定义 =2a ||=2a
方程 =1(a>0,b>0) =1(a>0,b>0) =1(a>0,b>0)
=1(a>0,b>0)
焦点
a,b,c关系
三、课堂练习
【例1】
已知双曲线两个焦点分别为F1(-5, 0), F2(5,0), 双曲线上一点P到F1, F2距离差的绝对值等于6,求双曲线的标准方程.
【例1】
已知双曲线两个焦点分别为F1(-5, 0), F2(5,0), 双曲线上一点P到F1, F2距离差的绝对值等于6,求双曲线的标准方程.
【例2】
已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.
【例2】
已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.
四、课后小结
1、双曲线的定义;
2、双曲线的标准方程;
3、双曲线与椭圆的区别.
五、课后作业
P121 练习4
谢 谢
双曲线及其标准方程
Standard equation
Hyperbola
一、类比探究
思 考
我们知道
与两个定点距离的和为非零常数(大于两个定点间的距离)的点的轨迹是椭圆。
那么,与两个定点距离的差为非零常数的点的轨迹是什么?
点的轨迹(椭圆):
与两个定点距离的和为非零常数
点的轨迹(双曲线一支):
与两个定点距离的差为非零常数
二、新知探究
1、双曲线的定义:
我们把平面内与两个定点F1、F2的距离的差的绝对值等于常数(小于| F1F2 |) 的点的轨迹叫做双曲线, 这两个定点叫做双曲线的焦点, 两焦点间的距离叫做双曲线的焦距.
2、双曲线的标准方程:
思 考
x
y
我们应该建立怎样的平面直角坐标系来方面求出双曲线的标准方程?
x
y
设P(x, y)是双曲线上任意一点,双曲线的焦距为2c(c>0),那么,焦点F1, F2的坐标分别是(-c, 0), (c, 0),又设点P与F1, F2的距离的差的绝对值等于常数2a.
2、双曲线的标准方程:
思 考
2、双曲线的标准方程:
类比焦点在y轴上的椭圆标准方程,如图, 双曲线的焦点分别是F1(0, -c), F2 (0, c), a, b的意义同上,这时双曲线的标准方程是什么?
x
y
思 考
2、双曲线的标准方程:
类比焦点在y轴上的椭圆标准方程,如图, 双曲线的焦点分别是F1(0, -c), F2 (0, c), a, b的意义同上,这时双曲线的标准方程是什么?
x
y
3、椭圆方程与双曲线方程之间的区别:
椭圆 双曲线
定义
方程
焦点
a,b,c关系
3、椭圆方程与双曲线方程之间的区别:
椭圆 双曲线
定义 =2a ||=2a
方程 =1(a>0,b>0) =1(a>0,b>0) =1(a>0,b>0)
=1(a>0,b>0)
焦点
a,b,c关系
三、课堂练习
【例1】
已知双曲线两个焦点分别为F1(-5, 0), F2(5,0), 双曲线上一点P到F1, F2距离差的绝对值等于6,求双曲线的标准方程.
【例1】
已知双曲线两个焦点分别为F1(-5, 0), F2(5,0), 双曲线上一点P到F1, F2距离差的绝对值等于6,求双曲线的标准方程.
【例2】
已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.
【例2】
已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.
四、课后小结
1、双曲线的定义;
2、双曲线的标准方程;
3、双曲线与椭圆的区别.
五、课后作业
P121 练习4
谢 谢
