6.4生活中的圆周运动 课件(27页)
文档属性
| 名称 | 6.4生活中的圆周运动 课件(27页) |  | |
| 格式 | pptx | ||
| 文件大小 | 15.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-06 11:24:05 | ||
图片预览








文档简介
(共27张PPT)
第4节 生活中的圆周运动
年 级:高一
学 科:物理(人教版)
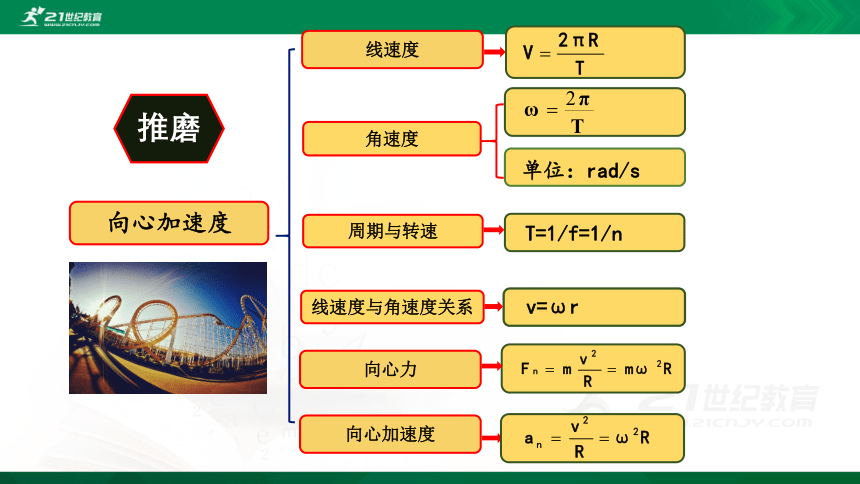
向心加速度
线速度
角速度
线速度与角速度关系
推磨
周期与转速
单位:rad/s
T=1/f=1/n
v=ωr
向心力
向心加速度
一、火车转弯
在铁路弯道处,稍微留意一下,就能发现内、外轨道的高度略有不同。这是为什么呢?
内侧轨道
外侧轨道
水平线
假设内、外轨道的倾斜程度与水平线之间的角度为
火车转弯时的轨迹可以视为一段小圆弧,故我们可以将火车的转弯视为很小的一段圆周运动。
转弯的轨道
一、火车转弯
火车转弯时的轨迹可以视为一段小圆弧,故我们可以将火车的转弯视为很小的一段圆周运动,满足圆周运动的规律,可以用圆周运动的方法分析。
转弯的轨迹
一、火车转弯
火车的车轮上两侧都有突出的轮缘。
车轮的结构
一、火车转弯
水平的转弯轨道
如果铁路弯道的内外轨一样高,转弯时,外侧车轮的轮缘挤压外轨,使外轨发生弹性形变,外轨对轮缘的弹力是火车转弯所需向心力的主要来源。但火车质量太大,靠这种办法得到向心力,将会使轮缘与外轨间的相互作用力过大,不仅铁轨和车轮极易受损,还可能使火车侧翻。
内侧轨道
外侧轨道
一、火车转弯
如果在弯道处使外轨略高于内轨,火车转弯时铁轨对火车的支持力FN的方向不再是竖直的,而是斜向弯道的内侧,它与重力G的合力指向圆心,为火车转弯提供了一部分向心力。这就减轻了轮缘与外轨间的挤压。
G
FN
在修筑铁路时,要根据弯道的半径和规定的行驶速度,适当选择内外轨的高度差,使转弯时所需的向心力几乎完全由重力G和支持力 FN的合力来提供。
倾斜的转弯轨道
一、火车转弯
在修筑铁路时,要根据弯道的半径和规定的行驶速度,适当选择内外轨的高度差,使转弯时所需的向心力几乎完全由重力G和支持力 FN的合力来提供。
G
FN
倾斜的转弯轨道
汽车过拱形桥时的运动也可以看作圆周运动。质量为m的汽车在拱形桥上以速度v前进,设桥面的圆弧半径为 r,分析汽车通过桥的最高点时对桥的压力。
O
r
桥对车的支持力:
车对桥的压力:
由此可得,汽车对桥的压力FN′小于汽车所受的重力G,而且汽车的速度越大,汽车对桥的压力越小。
二、汽车过拱形桥
拱形桥面
汽车过拱形桥时的运动也可以看作圆周运动。质量为m的汽车在拱形桥上以速度v前进,设桥面的圆弧半径为 r,分析汽车通过桥的最高点时对桥的压力。
O
r
当桥对车的支持力FN刚好等于零时,即此时车刚刚离开桥面,有:
二、汽车过拱形桥
此后车离开桥面,做平抛运动,直至落回水平地面。
拱形桥面
二、汽车过拱形桥
拱形桥面
地球可以看作一个巨大的拱形桥,桥面的半径就是地球的半径R(约为 6400 km)。地面上有一辆汽车在行驶,所受重力G = mg,地面对它的支持力是FN 。根据上面的分析,汽车速度越大,地面对它的支持力就越小。
r
O
FN
G
桥对车的支持力:
车对桥的压力:
二、汽车过拱形桥
拱形桥面
r
O
FN
G
桥对车的支持力:
车对桥的压力:
会不会出现这样的情况:速度大到一定程度时,地面对车的支持力是0?这时驾驶员与座椅之间的压力是多少?驾驶员躯体各部分之间的压力是多少?他这时有什么感觉?
公路在通过小型水库泄洪闸的下游时常常要修建凹形路面,也叫“过水路面”。汽车通过凹形路面的最低点时,车对地面的压力比汽车所受的重力大些还是小些?
O
r
二、汽车过凹形地面
凹形路面
故汽车通过凹形路面的最低点时,车对地面的压力比汽车所受的重力要大一些。
三、航天器中的失重现象
失重现象
r ≈ R
O
以绕地球做匀速圆周运动的宇宙飞船为例,当飞船距地面高度为100 200 km 时,它的轨道半径近似等于地球半径R,航天员受到的地球引力近似等于他在地面受到的重力mg。
三、航天器中的失重现象
失重现象
对飞船:
对飞船内的航天员:
代入
故航天员处于完全失重状态。
r ≈ R
正是由于地球引力的存在,才使航天器连同其中的乘员有可能做环绕地球的圆周运动。
四、离心运动
离心现象
做圆周运动的物体,由于惯性,总有沿着切线方向飞出去的趋势。但是物体没有飞出去,这是因为有其他力提供的向心力在拉着它,使它与圆心的距离保持不变。一旦提供的向心力突然消失,物体就会沿切线方向飞出去。
四、离心运动
供需关系图
提
提
提
物体沿切线方向沿直线飞出;
物体做离心运动,逐渐远离圆心;
物体做圆周运动;
提
物体做近心运动,逐渐靠近圆心。
F 是由指向圆心的合力来充当的,可以是重力、拉力、摩擦力等;
提
F 是由物体的运动速度来决定的,即:
需
F =
需
四、离心运动
离心运动的应用
1. 洗衣机脱水时利用离心运动把附着在物体上的水分甩掉;
2.纺织厂也用这样的方法使棉纱、毛线、纺织品干燥。
3. 在炼钢厂中,把熔化的钢水浇入圆柱形模子,模子沿圆柱的中心轴线高速旋转,钢水由于离心运动趋于周壁,冷却后就形成无缝钢管。
4.水泥管道和水泥电线杆的制造也可以采用这种离心制管技术。借助离心机,医务人员可以从血液中分离出血浆和红细胞。
离心运动的危害
在水平公路上行驶的汽车,如果转弯时速度过大,所需向心力F很大,如果大于了最大静摩擦力Fmax,汽车将做离心运动而造成事故。因此,在公路弯道,车辆不允许超过规定的速度。
高速转动的砂轮、飞轮等,都不得超过允许的最大转速。转速过高时,砂轮、飞轮内部分子间的相互作用力不足以提供所需向心力,离心运动会使它们破裂,酿成事故。
四、离心运动
教材第38页课后习题
1. 如果高速转动的飞轮的重心不在转轴上,运行将不稳定,而且轴承会受到很大的作用力,加速磨损。图中飞轮半径 r = 20 cm,OO′为转动轴。正常工作时转动轴受到的水平作用力可以认为是0。假想在飞轮的边缘固定一个质量m = 0.01 kg 的小螺丝钉P,当飞轮转速n = 1000 r/s 时,转动轴OO′受到多大的力?
五、练习与应用
教材第38页课后习题
2. 有一种叫“飞椅”的游乐项目。长为L的钢绳一端系着座椅,另一端固定在半径为 r 的水平转盘边缘。转盘可绕穿过其中心的竖直轴转动。当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ。不计钢绳的重力。分析转盘转动的角速度ω与夹角θ的关系。
五、练习与应用
教材第39页课后习题
3. 质量为 2.0×10 kg 的汽车在水平公路上行驶,轮胎与路面间的最大静摩擦力为1.4×10 N。汽车经过半径为50 m的弯路时,如果车速达到72 km/h,这辆车会不会发生侧滑?
五、练习与应用
3
4
会发生侧滑。
教材第39页课后习题
4. 有一辆质量为 800 kg 的小汽车驶上圆弧半径为 50 m 的拱桥。
五、练习与应用
(1)汽车到达桥顶时速度为5 m/s,汽车对桥的压力是多大?
(2)汽车以多大速度经过桥顶时恰好腾空,对桥没有压力?
(3)汽车对地面的压力过小是不安全的。从这个角度讲,汽车过桥时的速度不能过大。对于同样的车速,拱桥圆弧的半径大些比较安全,还是小些比较安全?
(4)如果拱桥的半径增大到与地球半径R一样,汽车要在桥面上腾空,速度要多大?
解(1):
教材第39页课后习题
4. 有一辆质量为 800 kg 的小汽车驶上圆弧半径为 50 m 的拱桥。
五、练习与应用
(1)汽车到达桥顶时速度为5 m/s,汽车对桥的压力是多大?
(2)汽车以多大速度经过桥顶时恰好腾空,对桥没有压力?
(3)汽车对地面的压力过小是不安全的。从这个角度讲,汽车过桥时的速度不能过大。对于同样的车速,拱桥圆弧的半径大些比较安全,还是小些比较安全?
(4)如果拱桥的半径增大到与地球半径R一样,汽车要在桥面上腾空,速度要多大?
解(2):
令
教材第39页课后习题
4. 有一辆质量为 800 kg 的小汽车驶上圆弧半径为 50 m 的拱桥。
五、练习与应用
(1)汽车到达桥顶时速度为5 m/s,汽车对桥的压力是多大?
(2)汽车以多大速度经过桥顶时恰好腾空,对桥没有压力?
(3)汽车对地面的压力过小是不安全的。从这个角度讲,汽车过桥时的速度不能过大。对于同样的车速,拱桥圆弧的半径大些比较安全,还是小些比较安全?
(4)如果拱桥的半径增大到与地球半径R一样,汽车要在桥面上腾空,速度要多大?
解(3):
可得:当半径r越大时,支持力FN越大,汽车行驶越安全。
教材第39页课后习题
4. 有一辆质量为 800 kg 的小汽车驶上圆弧半径为 50 m 的拱桥。
五、练习与应用
(1)汽车到达桥顶时速度为5 m/s,汽车对桥的压力是多大?
(2)汽车以多大速度经过桥顶时恰好腾空,对桥没有压力?
(3)汽车对地面的压力过小是不安全的。从这个角度讲,汽车过桥时的速度不能过大。对于同样的车速,拱桥圆弧的半径大些比较安全,还是小些比较安全?
(4)如果拱桥的半径增大到与地球半径R一样,汽车要在桥面上腾空,速度要多大?
解(4):
令
教材第39页课后习题
5. 质量为25 kg 的小孩坐在秋千上,小孩离系绳子的横梁2.5 m。秋千摆到最低点时,如果小孩运动速度的大小是5 m/s,他对秋千的压力是多大?
五、练习与应用
第4节 生活中的圆周运动
年 级:高一
学 科:物理(人教版)
向心加速度
线速度
角速度
线速度与角速度关系
推磨
周期与转速
单位:rad/s
T=1/f=1/n
v=ωr
向心力
向心加速度
一、火车转弯
在铁路弯道处,稍微留意一下,就能发现内、外轨道的高度略有不同。这是为什么呢?
内侧轨道
外侧轨道
水平线
假设内、外轨道的倾斜程度与水平线之间的角度为
火车转弯时的轨迹可以视为一段小圆弧,故我们可以将火车的转弯视为很小的一段圆周运动。
转弯的轨道
一、火车转弯
火车转弯时的轨迹可以视为一段小圆弧,故我们可以将火车的转弯视为很小的一段圆周运动,满足圆周运动的规律,可以用圆周运动的方法分析。
转弯的轨迹
一、火车转弯
火车的车轮上两侧都有突出的轮缘。
车轮的结构
一、火车转弯
水平的转弯轨道
如果铁路弯道的内外轨一样高,转弯时,外侧车轮的轮缘挤压外轨,使外轨发生弹性形变,外轨对轮缘的弹力是火车转弯所需向心力的主要来源。但火车质量太大,靠这种办法得到向心力,将会使轮缘与外轨间的相互作用力过大,不仅铁轨和车轮极易受损,还可能使火车侧翻。
内侧轨道
外侧轨道
一、火车转弯
如果在弯道处使外轨略高于内轨,火车转弯时铁轨对火车的支持力FN的方向不再是竖直的,而是斜向弯道的内侧,它与重力G的合力指向圆心,为火车转弯提供了一部分向心力。这就减轻了轮缘与外轨间的挤压。
G
FN
在修筑铁路时,要根据弯道的半径和规定的行驶速度,适当选择内外轨的高度差,使转弯时所需的向心力几乎完全由重力G和支持力 FN的合力来提供。
倾斜的转弯轨道
一、火车转弯
在修筑铁路时,要根据弯道的半径和规定的行驶速度,适当选择内外轨的高度差,使转弯时所需的向心力几乎完全由重力G和支持力 FN的合力来提供。
G
FN
倾斜的转弯轨道
汽车过拱形桥时的运动也可以看作圆周运动。质量为m的汽车在拱形桥上以速度v前进,设桥面的圆弧半径为 r,分析汽车通过桥的最高点时对桥的压力。
O
r
桥对车的支持力:
车对桥的压力:
由此可得,汽车对桥的压力FN′小于汽车所受的重力G,而且汽车的速度越大,汽车对桥的压力越小。
二、汽车过拱形桥
拱形桥面
汽车过拱形桥时的运动也可以看作圆周运动。质量为m的汽车在拱形桥上以速度v前进,设桥面的圆弧半径为 r,分析汽车通过桥的最高点时对桥的压力。
O
r
当桥对车的支持力FN刚好等于零时,即此时车刚刚离开桥面,有:
二、汽车过拱形桥
此后车离开桥面,做平抛运动,直至落回水平地面。
拱形桥面
二、汽车过拱形桥
拱形桥面
地球可以看作一个巨大的拱形桥,桥面的半径就是地球的半径R(约为 6400 km)。地面上有一辆汽车在行驶,所受重力G = mg,地面对它的支持力是FN 。根据上面的分析,汽车速度越大,地面对它的支持力就越小。
r
O
FN
G
桥对车的支持力:
车对桥的压力:
二、汽车过拱形桥
拱形桥面
r
O
FN
G
桥对车的支持力:
车对桥的压力:
会不会出现这样的情况:速度大到一定程度时,地面对车的支持力是0?这时驾驶员与座椅之间的压力是多少?驾驶员躯体各部分之间的压力是多少?他这时有什么感觉?
公路在通过小型水库泄洪闸的下游时常常要修建凹形路面,也叫“过水路面”。汽车通过凹形路面的最低点时,车对地面的压力比汽车所受的重力大些还是小些?
O
r
二、汽车过凹形地面
凹形路面
故汽车通过凹形路面的最低点时,车对地面的压力比汽车所受的重力要大一些。
三、航天器中的失重现象
失重现象
r ≈ R
O
以绕地球做匀速圆周运动的宇宙飞船为例,当飞船距地面高度为100 200 km 时,它的轨道半径近似等于地球半径R,航天员受到的地球引力近似等于他在地面受到的重力mg。
三、航天器中的失重现象
失重现象
对飞船:
对飞船内的航天员:
代入
故航天员处于完全失重状态。
r ≈ R
正是由于地球引力的存在,才使航天器连同其中的乘员有可能做环绕地球的圆周运动。
四、离心运动
离心现象
做圆周运动的物体,由于惯性,总有沿着切线方向飞出去的趋势。但是物体没有飞出去,这是因为有其他力提供的向心力在拉着它,使它与圆心的距离保持不变。一旦提供的向心力突然消失,物体就会沿切线方向飞出去。
四、离心运动
供需关系图
提
提
提
物体沿切线方向沿直线飞出;
物体做离心运动,逐渐远离圆心;
物体做圆周运动;
提
物体做近心运动,逐渐靠近圆心。
F 是由指向圆心的合力来充当的,可以是重力、拉力、摩擦力等;
提
F 是由物体的运动速度来决定的,即:
需
F =
需
四、离心运动
离心运动的应用
1. 洗衣机脱水时利用离心运动把附着在物体上的水分甩掉;
2.纺织厂也用这样的方法使棉纱、毛线、纺织品干燥。
3. 在炼钢厂中,把熔化的钢水浇入圆柱形模子,模子沿圆柱的中心轴线高速旋转,钢水由于离心运动趋于周壁,冷却后就形成无缝钢管。
4.水泥管道和水泥电线杆的制造也可以采用这种离心制管技术。借助离心机,医务人员可以从血液中分离出血浆和红细胞。
离心运动的危害
在水平公路上行驶的汽车,如果转弯时速度过大,所需向心力F很大,如果大于了最大静摩擦力Fmax,汽车将做离心运动而造成事故。因此,在公路弯道,车辆不允许超过规定的速度。
高速转动的砂轮、飞轮等,都不得超过允许的最大转速。转速过高时,砂轮、飞轮内部分子间的相互作用力不足以提供所需向心力,离心运动会使它们破裂,酿成事故。
四、离心运动
教材第38页课后习题
1. 如果高速转动的飞轮的重心不在转轴上,运行将不稳定,而且轴承会受到很大的作用力,加速磨损。图中飞轮半径 r = 20 cm,OO′为转动轴。正常工作时转动轴受到的水平作用力可以认为是0。假想在飞轮的边缘固定一个质量m = 0.01 kg 的小螺丝钉P,当飞轮转速n = 1000 r/s 时,转动轴OO′受到多大的力?
五、练习与应用
教材第38页课后习题
2. 有一种叫“飞椅”的游乐项目。长为L的钢绳一端系着座椅,另一端固定在半径为 r 的水平转盘边缘。转盘可绕穿过其中心的竖直轴转动。当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ。不计钢绳的重力。分析转盘转动的角速度ω与夹角θ的关系。
五、练习与应用
教材第39页课后习题
3. 质量为 2.0×10 kg 的汽车在水平公路上行驶,轮胎与路面间的最大静摩擦力为1.4×10 N。汽车经过半径为50 m的弯路时,如果车速达到72 km/h,这辆车会不会发生侧滑?
五、练习与应用
3
4
会发生侧滑。
教材第39页课后习题
4. 有一辆质量为 800 kg 的小汽车驶上圆弧半径为 50 m 的拱桥。
五、练习与应用
(1)汽车到达桥顶时速度为5 m/s,汽车对桥的压力是多大?
(2)汽车以多大速度经过桥顶时恰好腾空,对桥没有压力?
(3)汽车对地面的压力过小是不安全的。从这个角度讲,汽车过桥时的速度不能过大。对于同样的车速,拱桥圆弧的半径大些比较安全,还是小些比较安全?
(4)如果拱桥的半径增大到与地球半径R一样,汽车要在桥面上腾空,速度要多大?
解(1):
教材第39页课后习题
4. 有一辆质量为 800 kg 的小汽车驶上圆弧半径为 50 m 的拱桥。
五、练习与应用
(1)汽车到达桥顶时速度为5 m/s,汽车对桥的压力是多大?
(2)汽车以多大速度经过桥顶时恰好腾空,对桥没有压力?
(3)汽车对地面的压力过小是不安全的。从这个角度讲,汽车过桥时的速度不能过大。对于同样的车速,拱桥圆弧的半径大些比较安全,还是小些比较安全?
(4)如果拱桥的半径增大到与地球半径R一样,汽车要在桥面上腾空,速度要多大?
解(2):
令
教材第39页课后习题
4. 有一辆质量为 800 kg 的小汽车驶上圆弧半径为 50 m 的拱桥。
五、练习与应用
(1)汽车到达桥顶时速度为5 m/s,汽车对桥的压力是多大?
(2)汽车以多大速度经过桥顶时恰好腾空,对桥没有压力?
(3)汽车对地面的压力过小是不安全的。从这个角度讲,汽车过桥时的速度不能过大。对于同样的车速,拱桥圆弧的半径大些比较安全,还是小些比较安全?
(4)如果拱桥的半径增大到与地球半径R一样,汽车要在桥面上腾空,速度要多大?
解(3):
可得:当半径r越大时,支持力FN越大,汽车行驶越安全。
教材第39页课后习题
4. 有一辆质量为 800 kg 的小汽车驶上圆弧半径为 50 m 的拱桥。
五、练习与应用
(1)汽车到达桥顶时速度为5 m/s,汽车对桥的压力是多大?
(2)汽车以多大速度经过桥顶时恰好腾空,对桥没有压力?
(3)汽车对地面的压力过小是不安全的。从这个角度讲,汽车过桥时的速度不能过大。对于同样的车速,拱桥圆弧的半径大些比较安全,还是小些比较安全?
(4)如果拱桥的半径增大到与地球半径R一样,汽车要在桥面上腾空,速度要多大?
解(4):
令
教材第39页课后习题
5. 质量为25 kg 的小孩坐在秋千上,小孩离系绳子的横梁2.5 m。秋千摆到最低点时,如果小孩运动速度的大小是5 m/s,他对秋千的压力是多大?
五、练习与应用
