【解析版】河北省唐山一中2014届高三下学期开学调研考试数学(理)试题
文档属性
| 名称 | 【解析版】河北省唐山一中2014届高三下学期开学调研考试数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 508.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-06 16:34:36 | ||
图片预览




文档简介
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知复数,是的共轭复数,且 则a、b的值分别为( )
A. B. C. D.
2.已知等差数列中,, 则的值是( )
A. 15 B.30 C.31 D.64
3.实数满足条件,则的最小值为( )
A.16 B.4 C.1 D.
【答案】D
【解析】
4.二项式展开式中的常数项是( )
A.第7项 B.第8项 C.第9项 D.第10项
5.直线的方向向量为且过抛物线的焦点,则直线与抛物线围成的封闭图形面积为( )
A. B. C. D.
.联立直线与抛物线方程,则可知直线与抛物线围
6.已知,则是成立的( )
A 充要条件 B 充分不必要条件 C 必要不充分条件 D.既不充分也不必要条件
7.设m,n分别是先后抛掷一枚骰子得到的点数,则在先后两次出现的点数中有5的条件下,方程有实根的概率为( )
A. B. C. D.
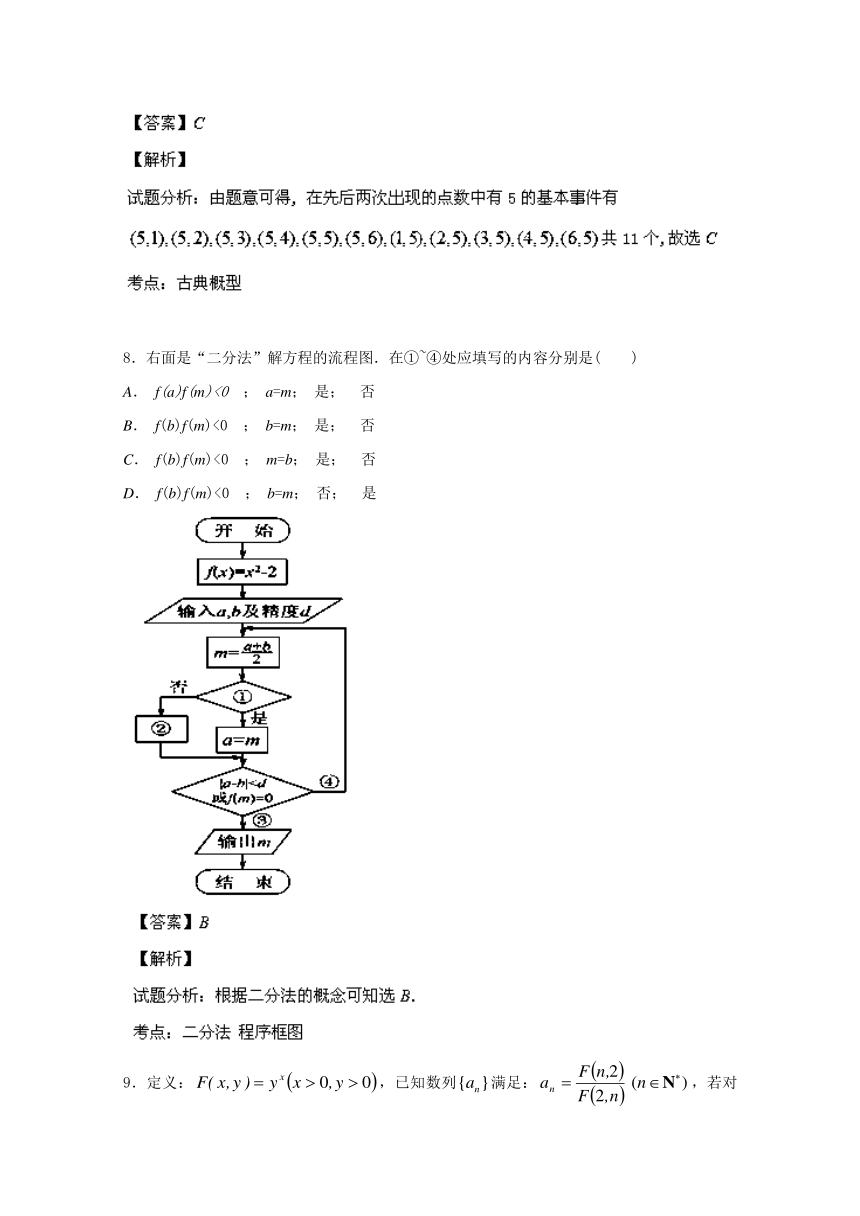
8.右面是“二分法”解方程的流程图.在①~④处应填写的内容分别是( )
A. f(a)f(m)<0 ; a=m; 是; 否
B. f(b)f(m)<0 ; b=m; 是; 否
C. f(b)f(m)<0 ; m=b; 是; 否
D. f(b)f(m)<0 ; b=m; 否; 是
9.定义:,已知数列满足:,若对任意正整数,都有成立,则的值为( )
A. B. C. D.
10.如图,正方体的棱长为,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( )
A. B. C. D.
11.已知,,规定:当时, ;当时, ,则( )
A. 有最小值,最大值1 B. 有最大值1,无最小值
C. 有最小值,无最大值 D. 有最大值,无最小值
12. 已知双曲线上一点,过双曲线中心的直线交双曲线于两点,记直线的斜率分别为,当最小时,双曲线离心率为( )
A . B. C D
第Ⅱ卷(共90分)
二、填空题(每题4分,满分16分,将答案填在答题纸上)
13.已知函数满足=1 且,则=___________.
14.若,则满足不等式的m的取值范围为 .
15.把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的主视图与俯视图如右上图所示,则二面角 C-AB-D的正切值为 .
16.如右图,在直角梯形ABCD中,AB//DC,AD⊥AB , AD=DC=2,AB=3,点是梯形内或边界上的一个动点,点N是DC边的中点,则的最大值是________ .
三、解答题 (本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
17.(本题满分12分)若的图像与直线相切,并且切点横坐标依次成公差为的等差数列.
(1)求和的值;
(2) ABC中a、b、c分别是∠A、∠B、∠C的对边.若是函数图象的一个对称中心,且a=4,求ABC面积的最大值.
18. (本小题满分12分)某高校在2012年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
(1)分别求第3,4,5组的频率;
(2) 若该校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
(ⅰ) 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙恰有一人进入第二轮面试的概率;
(ⅱ) 学校决定在这已抽取到的6名学生中随机抽取2名学生接受考官L的面试,设第4组中有名学生被考官L面试,求的分布列和数学期望.
人的情况数和分别有0,1,2人是第四组的情况数,即可得到相应的概率,进而得到分布列,在把三种情
19.(本小题满分12分)如图,四棱锥中,底面为平行四边形,,,⊥底面.
(1)证明:平面平面;
(2)若二面角为,求与平面所成角的正弦值.
【解析】
20. (本小题满分12分)已知圆 ,若椭圆的右顶点为圆的圆心,离心率为.
(1)求椭圆C的方程;
(2)若存在直线,使得直线与椭圆分别交于两点,与圆分别交于两点,点在线段上,且,求圆的半径的取值范围.
【答案】(1) (2)
21.(本小题满分12分)设函数
(1)若关于x的不等式在有实数解,求实数m的取值范围;
(2)设,若关于x的方程至少有一个解,求p的最小值.
(3)证明不等式:
考点:导数 不等式 函数最值
请考生在22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.
22.(本小题满分10分)选修4-1:几何证明选讲.如图,是⊙的直径, 是⊙的切线,与的延长线交于点,为切点.若,,的平分线与和⊙分别交于点、,求的值.
23.(本小题满分10分)选修4-4:坐标系与参数方程选讲.
在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为.
求圆C的极坐标方程;
在以极点O为原点,以极轴为x轴正半轴建立的直角坐标系中,直线的参数方程为
(t为参数),直线与圆C相交于A,B两点,已知定点,求|MA|·|MB|.
24.(本小题满分10分)选修4—5:不等式选讲
设函数
(1)若时,解不等式;
(2)若不等式的对一切恒成立,求实数的取值范围
同课章节目录
