2022-2023学年 冀教版九年级数学下册 30.4二次函数的应用课后练习 (无答案)
文档属性
| 名称 | 2022-2023学年 冀教版九年级数学下册 30.4二次函数的应用课后练习 (无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 698.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 00:00:00 | ||
图片预览




文档简介
30.4二次函数的应用课后测评
班级:________ 姓名:________
一、单选题(共 10 小题)
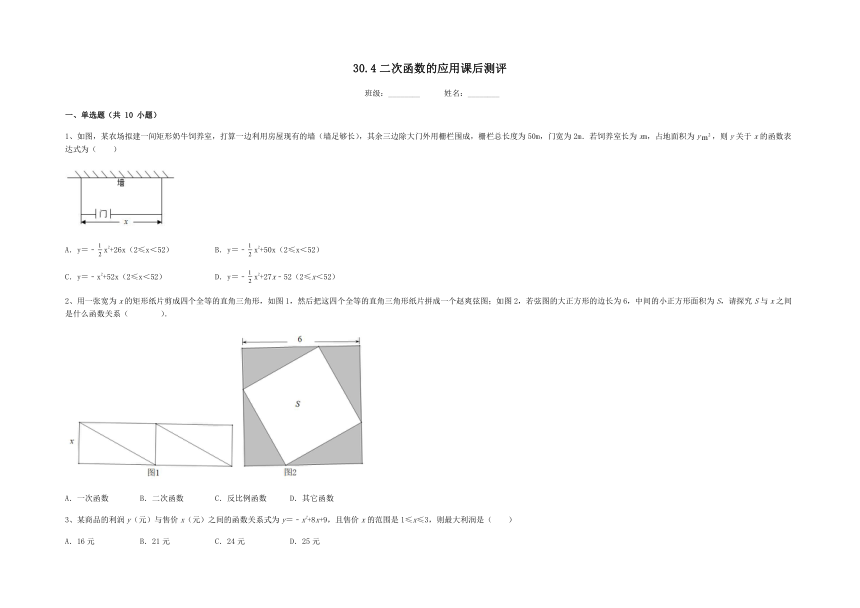
1、如图,某农场拟建一间矩形奶牛饲养室,打算一边利用房屋现有的墙(墙足够长),其余三边除大门外用栅栏围成,栅栏总长度为50m,门宽为2m.若饲养室长为xm,占地面积为y,则y关于x的函数表达式为( )
A.y=﹣x2+26x(2≤x<52) B.y=﹣x2+50x(2≤x<52)
C.y=﹣x2+52x(2≤x<52) D.y=﹣x2+27x﹣52(2≤x<52)
2、用一张宽为x的矩形纸片剪成四个全等的直角三角形,如图1,然后把这四个全等的直角三角形纸片拼成一个赵爽弦图;如图2,若弦图的大正方形的边长为6,中间的小正方形面积为S,请探究S与x之间是什么函数关系( ).
A.一次函数 B.二次函数 C.反比例函数 D.其它函数
3、某商品的利润y(元)与售价x(元)之间的函数关系式为y=﹣x2+8x+9,且售价x的范围是1≤x≤3,则最大利润是( )
A.16元 B.21元 C.24元 D.25元
4、如图,在平面直角坐标系中,点是抛物线的图象的顶点,点,的坐标分别为,,将沿轴向下平移使点平移到点,再绕点逆时针旋转,若此时点,的对应点,恰好落在抛物线上,则的值为( )
A. B.-1 C. D.-2
5、某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.则最大利润是( )
A.180 B.220 C.190 D.200
6、在同一平面直角坐标系中,若抛物线与关于y轴对称,则符合条件的m,n的值为( )
A.m=,n= B.m=5,n= -6 C.m= -1,n=6 D.m=1,n= -2
7、某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为和,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得最大利润为( )
A.45.51万元 B.45.56万元 C.45.6万元 D.45.606万元
8、根据防疫的相关要求,学生入校需晨检,体温超标的同学须进入临时隔离区进行留观.某校要建一个长方形临时隔离区,隔离区的一面利用学校边墙(墙长5米),其它三面用防疫隔离材料搭建,但要开一扇1米宽的进出口(不需材料),共用防疫隔离材料10米搭建的隔离区的面积最大为( )平方米.
A. B.25 C. D.15
9、小明以二次函数的图象为灵感为某葡萄酒大赛设计了一款杯子,如图为杯子的设计稿,若,,则杯子的高CE为( )
A.12 B.11 C.6 D.3
10、如图,四边形是边长为1的正方形,与x轴正半轴的夹角为,点B在抛物线()的图象上,则( )
A. B. C. D.
二、填空题(共 10 小题)
1、某公司经过市场调查,整理出某种商品在某个月的第x天与日销售量的相关信息如下表所示.已知商品的进价为20元/件,设该商品的日销售利润为y元.
第x天 售价(元/件) 日销售量件
(1)y与x的函数解析式为_______________;
(2)日销售的最大利润为_________元.
2、矩形ABCD中,点P从点A出发,沿AB边以每秒1个单位的速度向B点运动,至B点停止;同时点Q也从A点出发,以同样的速度沿A-D-C-B的路径运动,至B点停止,在此过程中△APQ的面积y与运动时间t的函数关系图象如图所示,则m的值为________
3、汽车刹车后行驶的距离s与行驶时间t(秒)的函数关系是s=15t﹣6t2,汽车从刹车到停下来所用时间是_______秒.
4、如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降________米,水面宽8米.
5、如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高时,水柱落点距O点;喷头高时,水柱落点距O点.那么喷头高_______________m时,水柱落点距O点.
6、如图,某农场要盖一排三间长方形的羊圈,打算一面利用旧墙,其余各面用木材围成栅栏,该计划用木材围成总长24m的栅栏,设面积为s(m2),垂直于墙的一边长为x(m)米.则s关于x的函数关系式:___(并写出自变量的取值范围)
7、如图,某拱桥呈抛物线形状,桥的最大高度是16米,跨度是40米,在线段上离中心处5米的地方,桥的高度是___________米.
8、如图是抛物线型拱桥,当拱顶高距离水面2m时,水面宽4m,如果水面上升1.5m,则水面宽度为________.
9、某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售价每涨价1元,月销售量就减少10千克,则月销售利润y(单位:元)与售价x(单位:元/千克)之间的函数解析式为_______________________
10、一座拱桥的轮廓是抛物线型(如图所示),桥高为8米,拱高6米,跨度20米.相邻两支柱间的距离均为5米,则支柱MN的高度为 _____米.
三、解答题(共 6 小题)
1、某企业接到生产一批设备的订单,要求不超过12天完成.这种设备的出厂价为1200元/台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台.若干天后,每台设备的生产成本将会增加,设第x天(x为整数)的生产成本为m(元台),m与x的关系如图所示.
(1)若第x天可以生产这种设备y台,则y与x的函数关系式为______,x的取值范围为______;
(2)第几天时,该企业当天的销售利润最大?最大利润为多少?
(3)求当天销售利润低于10800元的天数.
2、某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为.
(1)求雕塑高OA.
(2)求落水点C,D之间的距离.
(3)若需要在OD上的点E处竖立雕塑EF,,.问:顶部F是否会碰到水柱?请通过计算说明.
3、一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
4、掷实心球是兰州市高中阶段学校招生体育考试的选考项目.如图1是一名女生投掷实心球,实心求行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图2所示,抛出时起点处高度为,当水平距离为3m时,实心球行进至最高点3m处.
(1)求y关于x的函数表达式;
(2)根据兰州市高中阶段学校招生体有考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.70m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.
5、果园有果树60棵,现准备多种一些果树提高果园产量.如果多种树,那么树之间的距离和每棵果树所受光照就会减少,每棵果树的平均产量随之降低.根据经验,增种10棵果树时,果园内的每棵果树平均产量为.在确保每棵果树平均产量不低于的前提下,设增种果树x(且x为整数)棵,该果园每棵果树平均产量为,它们之间的函数关系满足如图所示的图象.
(1)图中点P所表示的实际意义是________________________,每增种1棵果树时,每棵果树平均产量减少____________;
(2)求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(3)当增种果树多少棵时,果园的总产量最大?最大产量是多少?
6、为积极响应国家“旧房改造”工程,该市推出《加快推进旧房改造工作的实施方案》推进新型城镇化建设,改善民生,优化城市建设.
(1)根据方案该市的旧房改造户数从2020年底的3万户增长到2022年底的4.32万户,求该市这两年旧房改造户数的平均年增长率;
(2)该市计划对某小区进行旧房改造,如果计划改造300户,计划投入改造费用平均20000元/户,且计划改造的户数每增加1户,投入改造费平均减少50元/户,求旧房改造申报的最高投入费用是多少元?
班级:________ 姓名:________
一、单选题(共 10 小题)
1、如图,某农场拟建一间矩形奶牛饲养室,打算一边利用房屋现有的墙(墙足够长),其余三边除大门外用栅栏围成,栅栏总长度为50m,门宽为2m.若饲养室长为xm,占地面积为y,则y关于x的函数表达式为( )
A.y=﹣x2+26x(2≤x<52) B.y=﹣x2+50x(2≤x<52)
C.y=﹣x2+52x(2≤x<52) D.y=﹣x2+27x﹣52(2≤x<52)
2、用一张宽为x的矩形纸片剪成四个全等的直角三角形,如图1,然后把这四个全等的直角三角形纸片拼成一个赵爽弦图;如图2,若弦图的大正方形的边长为6,中间的小正方形面积为S,请探究S与x之间是什么函数关系( ).
A.一次函数 B.二次函数 C.反比例函数 D.其它函数
3、某商品的利润y(元)与售价x(元)之间的函数关系式为y=﹣x2+8x+9,且售价x的范围是1≤x≤3,则最大利润是( )
A.16元 B.21元 C.24元 D.25元
4、如图,在平面直角坐标系中,点是抛物线的图象的顶点,点,的坐标分别为,,将沿轴向下平移使点平移到点,再绕点逆时针旋转,若此时点,的对应点,恰好落在抛物线上,则的值为( )
A. B.-1 C. D.-2
5、某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.则最大利润是( )
A.180 B.220 C.190 D.200
6、在同一平面直角坐标系中,若抛物线与关于y轴对称,则符合条件的m,n的值为( )
A.m=,n= B.m=5,n= -6 C.m= -1,n=6 D.m=1,n= -2
7、某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为和,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得最大利润为( )
A.45.51万元 B.45.56万元 C.45.6万元 D.45.606万元
8、根据防疫的相关要求,学生入校需晨检,体温超标的同学须进入临时隔离区进行留观.某校要建一个长方形临时隔离区,隔离区的一面利用学校边墙(墙长5米),其它三面用防疫隔离材料搭建,但要开一扇1米宽的进出口(不需材料),共用防疫隔离材料10米搭建的隔离区的面积最大为( )平方米.
A. B.25 C. D.15
9、小明以二次函数的图象为灵感为某葡萄酒大赛设计了一款杯子,如图为杯子的设计稿,若,,则杯子的高CE为( )
A.12 B.11 C.6 D.3
10、如图,四边形是边长为1的正方形,与x轴正半轴的夹角为,点B在抛物线()的图象上,则( )
A. B. C. D.
二、填空题(共 10 小题)
1、某公司经过市场调查,整理出某种商品在某个月的第x天与日销售量的相关信息如下表所示.已知商品的进价为20元/件,设该商品的日销售利润为y元.
第x天 售价(元/件) 日销售量件
(1)y与x的函数解析式为_______________;
(2)日销售的最大利润为_________元.
2、矩形ABCD中,点P从点A出发,沿AB边以每秒1个单位的速度向B点运动,至B点停止;同时点Q也从A点出发,以同样的速度沿A-D-C-B的路径运动,至B点停止,在此过程中△APQ的面积y与运动时间t的函数关系图象如图所示,则m的值为________
3、汽车刹车后行驶的距离s与行驶时间t(秒)的函数关系是s=15t﹣6t2,汽车从刹车到停下来所用时间是_______秒.
4、如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降________米,水面宽8米.
5、如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高时,水柱落点距O点;喷头高时,水柱落点距O点.那么喷头高_______________m时,水柱落点距O点.
6、如图,某农场要盖一排三间长方形的羊圈,打算一面利用旧墙,其余各面用木材围成栅栏,该计划用木材围成总长24m的栅栏,设面积为s(m2),垂直于墙的一边长为x(m)米.则s关于x的函数关系式:___(并写出自变量的取值范围)
7、如图,某拱桥呈抛物线形状,桥的最大高度是16米,跨度是40米,在线段上离中心处5米的地方,桥的高度是___________米.
8、如图是抛物线型拱桥,当拱顶高距离水面2m时,水面宽4m,如果水面上升1.5m,则水面宽度为________.
9、某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售价每涨价1元,月销售量就减少10千克,则月销售利润y(单位:元)与售价x(单位:元/千克)之间的函数解析式为_______________________
10、一座拱桥的轮廓是抛物线型(如图所示),桥高为8米,拱高6米,跨度20米.相邻两支柱间的距离均为5米,则支柱MN的高度为 _____米.
三、解答题(共 6 小题)
1、某企业接到生产一批设备的订单,要求不超过12天完成.这种设备的出厂价为1200元/台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台.若干天后,每台设备的生产成本将会增加,设第x天(x为整数)的生产成本为m(元台),m与x的关系如图所示.
(1)若第x天可以生产这种设备y台,则y与x的函数关系式为______,x的取值范围为______;
(2)第几天时,该企业当天的销售利润最大?最大利润为多少?
(3)求当天销售利润低于10800元的天数.
2、某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为.
(1)求雕塑高OA.
(2)求落水点C,D之间的距离.
(3)若需要在OD上的点E处竖立雕塑EF,,.问:顶部F是否会碰到水柱?请通过计算说明.
3、一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
4、掷实心球是兰州市高中阶段学校招生体育考试的选考项目.如图1是一名女生投掷实心球,实心求行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图2所示,抛出时起点处高度为,当水平距离为3m时,实心球行进至最高点3m处.
(1)求y关于x的函数表达式;
(2)根据兰州市高中阶段学校招生体有考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.70m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.
5、果园有果树60棵,现准备多种一些果树提高果园产量.如果多种树,那么树之间的距离和每棵果树所受光照就会减少,每棵果树的平均产量随之降低.根据经验,增种10棵果树时,果园内的每棵果树平均产量为.在确保每棵果树平均产量不低于的前提下,设增种果树x(且x为整数)棵,该果园每棵果树平均产量为,它们之间的函数关系满足如图所示的图象.
(1)图中点P所表示的实际意义是________________________,每增种1棵果树时,每棵果树平均产量减少____________;
(2)求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(3)当增种果树多少棵时,果园的总产量最大?最大产量是多少?
6、为积极响应国家“旧房改造”工程,该市推出《加快推进旧房改造工作的实施方案》推进新型城镇化建设,改善民生,优化城市建设.
(1)根据方案该市的旧房改造户数从2020年底的3万户增长到2022年底的4.32万户,求该市这两年旧房改造户数的平均年增长率;
(2)该市计划对某小区进行旧房改造,如果计划改造300户,计划投入改造费用平均20000元/户,且计划改造的户数每增加1户,投入改造费平均减少50元/户,求旧房改造申报的最高投入费用是多少元?
