2022-2023学年华东师大版九年级数学下册27.2与圆有关的位置关系练习 (无答案)
文档属性
| 名称 | 2022-2023学年华东师大版九年级数学下册27.2与圆有关的位置关系练习 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 431.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 09:28:53 | ||
图片预览



文档简介
27.2与圆有关的位置关系达标测评
班级:________ 姓名:________
一、单选题(共 10 小题)
1、如图,是的切线,点A为切点,交于点B,,点C在上,.则等于( )
A.20° B.25° C.30° D.50°
2、如图,直线AB是⊙O的切线,点C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为( )
A.30° B.35° C.40° D.45°
3、如图,的半径为4,圆心M的坐标为(6,8),P是⊙M上的任意一点,,且、与x轴分别交于A、B两点.若点A、B关于原点O对称,则长的最小值为( )
A.6 B.8 C.12 D.16
4、如图,与相切于点,若,则的度数为( )
A. B. C. D.
5、如图,半径的⊙M在轴上平移,且圆心M在x轴上,当⊙M与直线相切时,圆心M的坐标为( )
A.(0,0) B.(2,0) C.(-6,0) D.(2,0) 或(-6,0)
6、如图,、分别与相切于点、,连接并延长与交于点、,若,,则的值为( )
A. B. C. D.
7、如图,在Rt△ABC中,∠C=90°,BC=18,AC=24,点O在边AB上,且BO=2OA.以点O为圆心,r为半径作圆,如果⊙O与Rt△ABC的边有3个公共点,那么下列各值中,半径r不可以取的是( )
A.6 B.10 C.15 D.16
8、如图,在⊙O中,点C在优弧上,将弧沿BC折叠后刚好经过AB的中点D.若⊙O的半径为,AB=4,则BC的长是( )
A.2 B.3 C.4 D.3
9、如图,点P为⊙O外一点,过点P作⊙O的切线PA、PB,记切点为A、B,点C为⊙O上一点,连接AC、BC.若∠ACB=62°,则∠APB等于( )
A.68° B.64° C.58° D.56°
10、如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )
A.PA=PB B.∠BPD=∠APD C.AB⊥PD D.AB平分PD
二、填空题(共 8 小题)
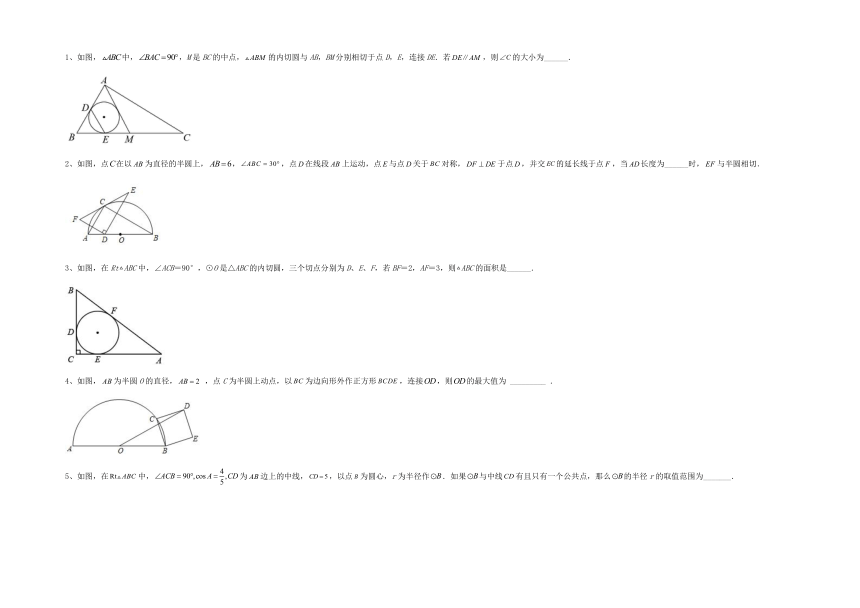
1、如图,中,,M是BC的中点,的内切圆与AB,BM分别相切于点D,E,连接DE.若,则的大小为______.
2、如图,点在以为直径的半圆上,,,点在线段上运动,点与点关于对称,于点,并交的延长线于点,当长度为______时,与半圆相切.
3、如图,在RtABC中,∠ACB=90°,⊙O是△ABC的内切圆,三个切点分别为D、E、F,若BF=2,AF=3,则ABC的面积是______.
4、如图,为半圆O的直径, ,点C为半圆上动点,以为边向形外作正方形,连接,则的最大值为 _________ .
5、如图,在中,为边上的中线,,以点为圆心,r为半径作.如果与中线有且只有一个公共点,那么的半径r的取值范围为_______.
6、在平面直角坐标系中,以点A(﹣2,3)为圆心、r为半径的圆与坐标轴恰好有三个公共点,那么r的值为_____.
7、在平面直角坐标系中,直线y=x-2与x轴、y轴分别交于点B、C,半径为1的⊙P的圆心P从点A(4,m )出发以每秒个单位长度的速度沿射线AC的方向运动,设点P运动的时间为t秒,则当t=_____秒时,⊙P与坐标轴相切.
8、有高度相同的一段方木和一段圆木,体积之比是1:1.在高度不变的情况下,如果将方木加工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得到的圆柱和长方体的体积之比为____.
三、解答题(共 6 小题)
1、如图,是的直径,过点作的切线,点是射线上的动点,连接,过点作//,交于点,连接.
(1)求证:是的切线;
(2)当的度数为______时,四边形是平行四边形.
2、如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A、B、D三点作⊙O,AE是⊙O的直径,连接DE.
(1)求证:AC是⊙O的切线
(2)若cosC,AC=24,求直径AE的长.
3、如图,是的直径,点C在上,的平分线交于点D,过点D作的垂线交的延长线于点E.
(1)证明:是的切线;
(2)已知 ,求的长.
4、如图,在中,.以AB为直径的与线段BC交于点D,过点D作,垂足为E,ED的延长线与AB的延长线交于点P.
(1)求证:直线PE是的切线;
(2)若的半径为6,,求CE的长.
5、如图,是的直径,为上一点,平分交于点.过点作交的延长线于点.
(1)求证:是的切线.
(2)若,,求的长.
6、定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是 ;(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形中,,,过点作垂线交的延长线于点,且,证明:四边形是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为的垂等四边形内接于⊙O中,.求⊙O的半径.
班级:________ 姓名:________
一、单选题(共 10 小题)
1、如图,是的切线,点A为切点,交于点B,,点C在上,.则等于( )
A.20° B.25° C.30° D.50°
2、如图,直线AB是⊙O的切线,点C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为( )
A.30° B.35° C.40° D.45°
3、如图,的半径为4,圆心M的坐标为(6,8),P是⊙M上的任意一点,,且、与x轴分别交于A、B两点.若点A、B关于原点O对称,则长的最小值为( )
A.6 B.8 C.12 D.16
4、如图,与相切于点,若,则的度数为( )
A. B. C. D.
5、如图,半径的⊙M在轴上平移,且圆心M在x轴上,当⊙M与直线相切时,圆心M的坐标为( )
A.(0,0) B.(2,0) C.(-6,0) D.(2,0) 或(-6,0)
6、如图,、分别与相切于点、,连接并延长与交于点、,若,,则的值为( )
A. B. C. D.
7、如图,在Rt△ABC中,∠C=90°,BC=18,AC=24,点O在边AB上,且BO=2OA.以点O为圆心,r为半径作圆,如果⊙O与Rt△ABC的边有3个公共点,那么下列各值中,半径r不可以取的是( )
A.6 B.10 C.15 D.16
8、如图,在⊙O中,点C在优弧上,将弧沿BC折叠后刚好经过AB的中点D.若⊙O的半径为,AB=4,则BC的长是( )
A.2 B.3 C.4 D.3
9、如图,点P为⊙O外一点,过点P作⊙O的切线PA、PB,记切点为A、B,点C为⊙O上一点,连接AC、BC.若∠ACB=62°,则∠APB等于( )
A.68° B.64° C.58° D.56°
10、如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )
A.PA=PB B.∠BPD=∠APD C.AB⊥PD D.AB平分PD
二、填空题(共 8 小题)
1、如图,中,,M是BC的中点,的内切圆与AB,BM分别相切于点D,E,连接DE.若,则的大小为______.
2、如图,点在以为直径的半圆上,,,点在线段上运动,点与点关于对称,于点,并交的延长线于点,当长度为______时,与半圆相切.
3、如图,在RtABC中,∠ACB=90°,⊙O是△ABC的内切圆,三个切点分别为D、E、F,若BF=2,AF=3,则ABC的面积是______.
4、如图,为半圆O的直径, ,点C为半圆上动点,以为边向形外作正方形,连接,则的最大值为 _________ .
5、如图,在中,为边上的中线,,以点为圆心,r为半径作.如果与中线有且只有一个公共点,那么的半径r的取值范围为_______.
6、在平面直角坐标系中,以点A(﹣2,3)为圆心、r为半径的圆与坐标轴恰好有三个公共点,那么r的值为_____.
7、在平面直角坐标系中,直线y=x-2与x轴、y轴分别交于点B、C,半径为1的⊙P的圆心P从点A(4,m )出发以每秒个单位长度的速度沿射线AC的方向运动,设点P运动的时间为t秒,则当t=_____秒时,⊙P与坐标轴相切.
8、有高度相同的一段方木和一段圆木,体积之比是1:1.在高度不变的情况下,如果将方木加工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得到的圆柱和长方体的体积之比为____.
三、解答题(共 6 小题)
1、如图,是的直径,过点作的切线,点是射线上的动点,连接,过点作//,交于点,连接.
(1)求证:是的切线;
(2)当的度数为______时,四边形是平行四边形.
2、如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A、B、D三点作⊙O,AE是⊙O的直径,连接DE.
(1)求证:AC是⊙O的切线
(2)若cosC,AC=24,求直径AE的长.
3、如图,是的直径,点C在上,的平分线交于点D,过点D作的垂线交的延长线于点E.
(1)证明:是的切线;
(2)已知 ,求的长.
4、如图,在中,.以AB为直径的与线段BC交于点D,过点D作,垂足为E,ED的延长线与AB的延长线交于点P.
(1)求证:直线PE是的切线;
(2)若的半径为6,,求CE的长.
5、如图,是的直径,为上一点,平分交于点.过点作交的延长线于点.
(1)求证:是的切线.
(2)若,,求的长.
6、定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是 ;(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形中,,,过点作垂线交的延长线于点,且,证明:四边形是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为的垂等四边形内接于⊙O中,.求⊙O的半径.
