北师大版八年级下册第一章 三角形的证明 单元测试卷(无答案)
文档属性
| 名称 | 北师大版八年级下册第一章 三角形的证明 单元测试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 115.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 10:09:56 | ||
图片预览

文档简介
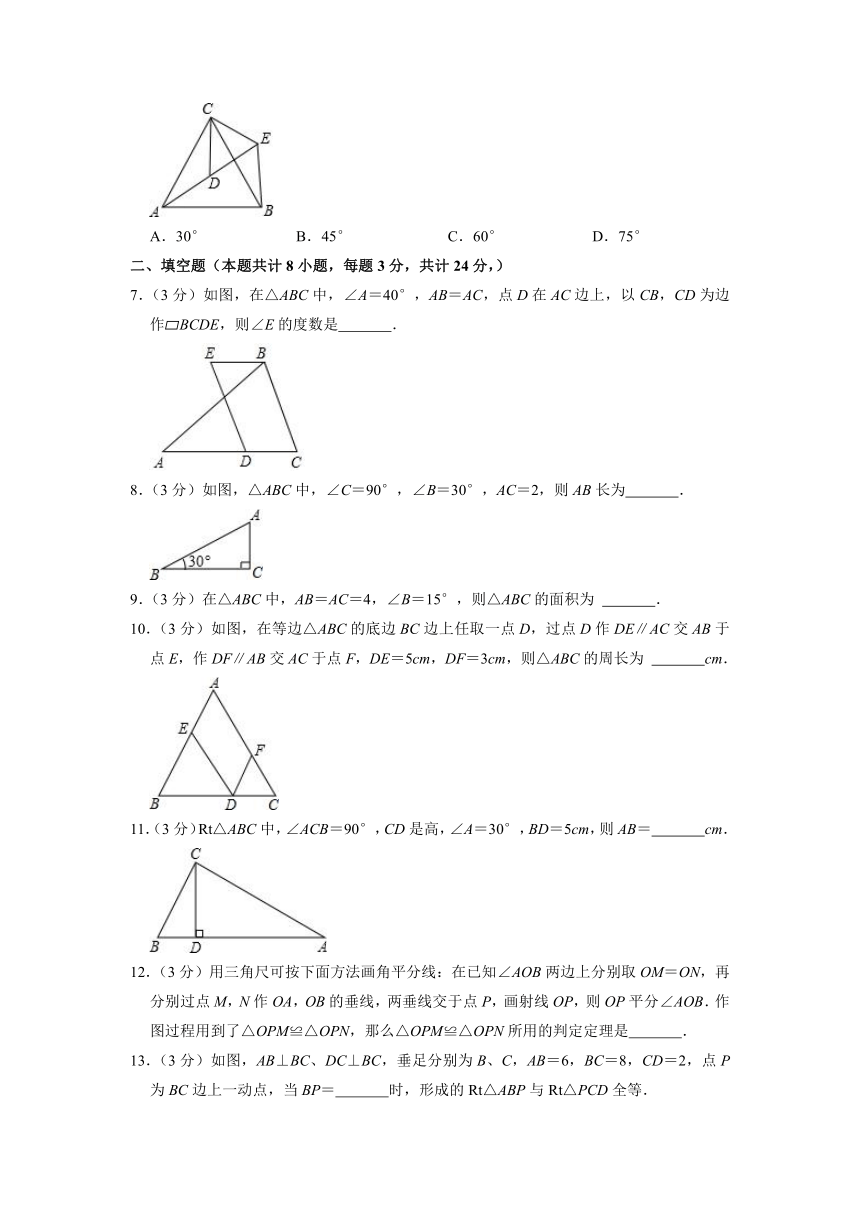
《第1章 三角形的证明》单元测试卷
一、选择题(本题共计6小题,每题3分,共计18分,)
1.(3分)已知直角三角形中30°角所对的直角边为2cm,则斜边的长为( )
A.2cm B.4cm C.6cm D.8cm
2.(3分)直角三角形的两条直角边分别12cm和16cm,斜边为20cm,则斜边上的高为( )
A.8cm B.10cm C.9.1cm D.9.6cm
3.(3分)如图等边△ABC边长为1cm,D、E分别是AB、AC上两点,将△ADE沿直线DE折叠,点A落在A′处,A在△ABC外,则阴影部分图形周长为( )
A.1cm B.1.5cm C.2cm D.3cm
4.(3分)如图,四边形ABCD是矩形,AB>BC,点P在直线CD上,则满足△PAB是等腰三角形的点P共有( )
A.3个 B.4个 C.5个 D.6个
5.(3分)如图,DE⊥AC,BF⊥AC,垂足分别是E,F,且DE=BF,若利用“HL”证明△DEC≌△BFA,则需添加的条件是( )
A.EC=FA B.DC=BA C.∠D=∠B D.∠DCE=∠BAF
6.(3分)如图,△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,则∠AEB的度数是( )
A.30° B.45° C.60° D.75°
二、填空题(本题共计8小题,每题3分,共计24分,)
7.(3分)如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作 BCDE,则∠E的度数是 .
8.(3分)如图,△ABC中,∠C=90°,∠B=30°,AC=2,则AB长为 .
9.(3分)在△ABC中,AB=AC=4,∠B=15°,则△ABC的面积为 .
10.(3分)如图,在等边△ABC的底边BC边上任取一点D,过点D作DE∥AC交AB于点E,作DF∥AB交AC于点F,DE=5cm,DF=3cm,则△ABC的周长为 cm.
11.(3分)Rt△ABC中,∠ACB=90°,CD是高,∠A=30°,BD=5cm,则AB= cm.
12.(3分)用三角尺可按下面方法画角平分线:在已知∠AOB两边上分别取OM=ON,再分别过点M,N作OA,OB的垂线,两垂线交于点P,画射线OP,则OP平分∠AOB.作图过程用到了△OPM≌△OPN,那么△OPM≌△OPN所用的判定定理是 .
13.(3分)如图,AB⊥BC、DC⊥BC,垂足分别为B、C,AB=6,BC=8,CD=2,点P为BC边上一动点,当BP= 时,形成的Rt△ABP与Rt△PCD全等.
14.(3分)如图,∠BCA=90°,CD⊥AB,E为AB的中点,∠DCA:∠BCD=3:1,∠DCE的度数为 .
三、解答题(本题共计7小题,共计78分,)
15.如图,在等边三角形ABC中,点E为CB边上一点(与点C不重合),点F是AC边上一点,若AB=5,BE=2,∠AEF=60°,求AF的长度.
16.如图,在四边形ABCD中,∠BAD=∠BCD=90°,O为BD的中点.
(1)若AC=8,BD=10,求△AOC的周长.
(2)若∠ABD=60°,∠CBD=50°,求∠AOC和∠OCA的度数.
17.已知:如图,△ABC是等边三角形,D是BC延长线上一点,连接AD,以AD为边作等边三角形ADE,连接CE.
(1)求证:AC+CD=CE;
(2)求∠DCE的度数.
18.如图,已知△ABC中,∠ACB=120°,CE平分∠ACB,AD∥EC,交BC的延长线于点D,
(1)求∠BCE的度数;
(2)试找出图中的等边三角形,并说明理由.
19.已知,如图所示,DE⊥AB于点E,DF⊥AC于点F,BE=CF,BD=CD.
(1)求证:DE=DF;
(2)求证:AD平分∠BAC.
20.如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE
(1)若AC=10,BD=8,求△BDE的周长;
(2)判断△BDE的形状,并说明理由.
21.八年级数学课上,老师出示了如下框中的题目.
小华与同桌小明讨论后,进行了如下解答:
(1)特殊情况入手探索:
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系.
请你直接写出结论:AE DB(填“>”,“<”或“=”).
(2)一般情况进行论证:
对原题中的一般情形,二人讨论后得出(1)中的结论仍然成立,并且可以通过构造一个三角形与△EBD全等来证明.以下是他们的部分证明过程:
证明:如图2,过点E作EF∥BC,交AC于点F.……(请完成余下的证明过程)
(3)应用结论解决问题:
在边长为3的等边三角形ABC中,点E在直线AB上,且AE=1,点D在直线BC上,ED=EC.则CD= (直接写出结果).
一、选择题(本题共计6小题,每题3分,共计18分,)
1.(3分)已知直角三角形中30°角所对的直角边为2cm,则斜边的长为( )
A.2cm B.4cm C.6cm D.8cm
2.(3分)直角三角形的两条直角边分别12cm和16cm,斜边为20cm,则斜边上的高为( )
A.8cm B.10cm C.9.1cm D.9.6cm
3.(3分)如图等边△ABC边长为1cm,D、E分别是AB、AC上两点,将△ADE沿直线DE折叠,点A落在A′处,A在△ABC外,则阴影部分图形周长为( )
A.1cm B.1.5cm C.2cm D.3cm
4.(3分)如图,四边形ABCD是矩形,AB>BC,点P在直线CD上,则满足△PAB是等腰三角形的点P共有( )
A.3个 B.4个 C.5个 D.6个
5.(3分)如图,DE⊥AC,BF⊥AC,垂足分别是E,F,且DE=BF,若利用“HL”证明△DEC≌△BFA,则需添加的条件是( )
A.EC=FA B.DC=BA C.∠D=∠B D.∠DCE=∠BAF
6.(3分)如图,△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,则∠AEB的度数是( )
A.30° B.45° C.60° D.75°
二、填空题(本题共计8小题,每题3分,共计24分,)
7.(3分)如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作 BCDE,则∠E的度数是 .
8.(3分)如图,△ABC中,∠C=90°,∠B=30°,AC=2,则AB长为 .
9.(3分)在△ABC中,AB=AC=4,∠B=15°,则△ABC的面积为 .
10.(3分)如图,在等边△ABC的底边BC边上任取一点D,过点D作DE∥AC交AB于点E,作DF∥AB交AC于点F,DE=5cm,DF=3cm,则△ABC的周长为 cm.
11.(3分)Rt△ABC中,∠ACB=90°,CD是高,∠A=30°,BD=5cm,则AB= cm.
12.(3分)用三角尺可按下面方法画角平分线:在已知∠AOB两边上分别取OM=ON,再分别过点M,N作OA,OB的垂线,两垂线交于点P,画射线OP,则OP平分∠AOB.作图过程用到了△OPM≌△OPN,那么△OPM≌△OPN所用的判定定理是 .
13.(3分)如图,AB⊥BC、DC⊥BC,垂足分别为B、C,AB=6,BC=8,CD=2,点P为BC边上一动点,当BP= 时,形成的Rt△ABP与Rt△PCD全等.
14.(3分)如图,∠BCA=90°,CD⊥AB,E为AB的中点,∠DCA:∠BCD=3:1,∠DCE的度数为 .
三、解答题(本题共计7小题,共计78分,)
15.如图,在等边三角形ABC中,点E为CB边上一点(与点C不重合),点F是AC边上一点,若AB=5,BE=2,∠AEF=60°,求AF的长度.
16.如图,在四边形ABCD中,∠BAD=∠BCD=90°,O为BD的中点.
(1)若AC=8,BD=10,求△AOC的周长.
(2)若∠ABD=60°,∠CBD=50°,求∠AOC和∠OCA的度数.
17.已知:如图,△ABC是等边三角形,D是BC延长线上一点,连接AD,以AD为边作等边三角形ADE,连接CE.
(1)求证:AC+CD=CE;
(2)求∠DCE的度数.
18.如图,已知△ABC中,∠ACB=120°,CE平分∠ACB,AD∥EC,交BC的延长线于点D,
(1)求∠BCE的度数;
(2)试找出图中的等边三角形,并说明理由.
19.已知,如图所示,DE⊥AB于点E,DF⊥AC于点F,BE=CF,BD=CD.
(1)求证:DE=DF;
(2)求证:AD平分∠BAC.
20.如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE
(1)若AC=10,BD=8,求△BDE的周长;
(2)判断△BDE的形状,并说明理由.
21.八年级数学课上,老师出示了如下框中的题目.
小华与同桌小明讨论后,进行了如下解答:
(1)特殊情况入手探索:
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系.
请你直接写出结论:AE DB(填“>”,“<”或“=”).
(2)一般情况进行论证:
对原题中的一般情形,二人讨论后得出(1)中的结论仍然成立,并且可以通过构造一个三角形与△EBD全等来证明.以下是他们的部分证明过程:
证明:如图2,过点E作EF∥BC,交AC于点F.……(请完成余下的证明过程)
(3)应用结论解决问题:
在边长为3的等边三角形ABC中,点E在直线AB上,且AE=1,点D在直线BC上,ED=EC.则CD= (直接写出结果).
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
