人教版八年级下册16.3二次根式的加减(第1课时)课件(共18张PPT)
文档属性
| 名称 | 人教版八年级下册16.3二次根式的加减(第1课时)课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
16.3 二根次式的加减
第1课时 二次根式的加减
学习目标
1、了解同类二次根式的意义。
2、能熟练进行二次根式的加减运算。
重点
二次根式加减法的运算。
难点
熟练进行二次根式加减法的运算。
问题1 满足什么条件的根式是最简二次根式
问题2 化简下列两组二次根式,每组化简后有什么共同特点
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
化简后被开方数相同
复习引入
合并同类项的过程是通过使用分配律来完成的!
同类项、合并同类项知识点回顾
合并同类项概念:
合并同类项注意事项:
1.合并同类项后,所得项的系数是合并前各同类项的系数的和。
2.合并同类项后,字母连同它的指数不变。
把多项式中的同类项合并成一项,叫做
合并同类项.
练一练:
1. 2x5-6x5+5x5 =
2. 3a2-4a2+a3 =
x5
a3-a2
同类项概念:
所含字母相同,并且相同字母的指数也相
同的项叫做同类项
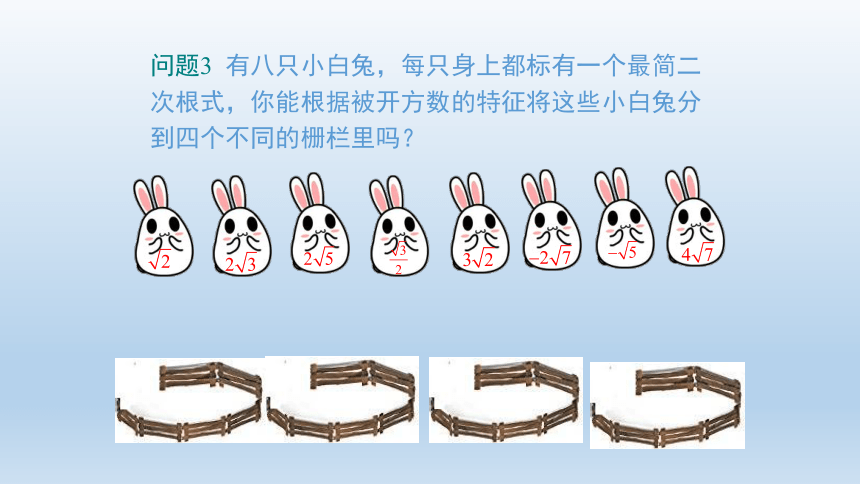
问题3 有八只小白兔,每只身上都标有一个最简二次根式,你能根据被开方数的特征将这些小白兔分到四个不同的栅栏里吗?
a
a
a
a
a
a
a
a
a
a
=
+
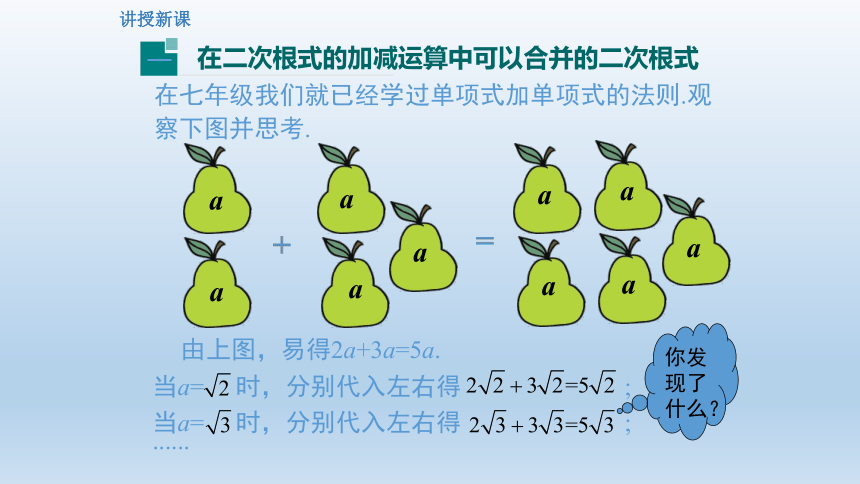
在七年级我们就已经学过单项式加单项式的法则.观察下图并思考.
由上图,易得2a+3a=5a.
当a= 时,分别代入左右得 ;
当a= 时,分别代入左右得 ;
......
讲授新课
在二次根式的加减运算中可以合并的二次根式
一
你发现了什么?
因为 ,两者可以合并为8
当a= ,b= 时,得2a+3b= .
a
2a+3b
b
=
+
b
b
a
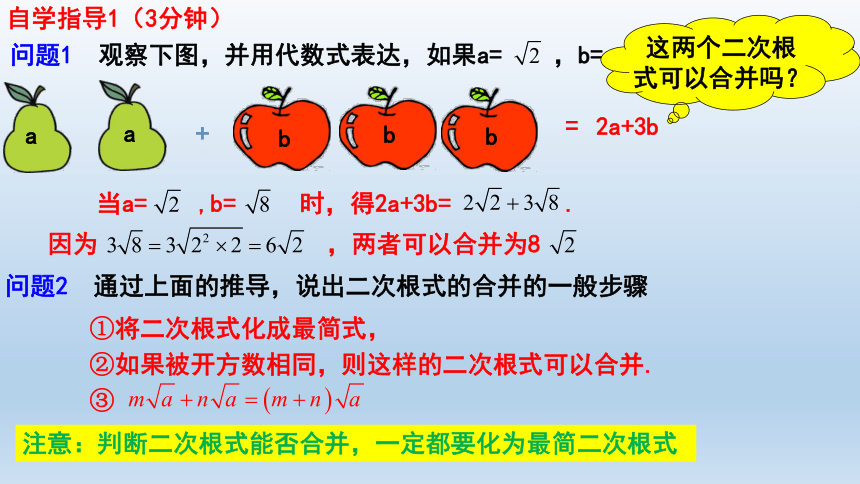
自学指导1(3分钟)
问题1 观察下图,并用代数式表达,如果a= ,b= 时,求代数式的值
这两个二次根式可以合并吗?
问题2 通过上面的推导,说出二次根式的合并的一般步骤
①将二次根式化成最简式,
②如果被开方数相同,则这样的二次根式可以合并.
③
注意:判断二次根式能否合并,一定都要化为最简二次根式
练一练
1.下列各式中,与 是同类二次根式的是( )
A. B. C. D.
D
2. 与最简二次根式 能合并,则m=_____.
1
3.下列二次根式,不能与 合并的是________(填
序号).
②⑤
二次根式的加减及其应用
二
思考 现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个分别是8dm2和18dm2的正方形木板?
7.5dm
5dm
问题1 怎样列式求两个正方形边长的和
S=8dm2
S=18dm2
问题2 所列算式能直接进行加减运算吗 如果不能,把式中各个二次根式化成最简二次根式后,再试一试(说出每步运算的依据).
(化成最简二次根式)
(逆用分配律)
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
解:列式如下:
在有理数范围内成立的运算律,在实数范围内仍然成立.
归纳总结
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
典例精析
例2 计算:
解:
例3 计算:
解:
有括号,先去括号
巩固提高
练习1 计算:
(1)
(2)
.
(3)
(4)
1.计算:(1) (2)
(3) (4)
解:
解:
5.计算:
解:
二次根式的加减与整式的加减根据都是分配律,它们的运算实质也基本相同。
二次根式的加减即为对同类二次根式的合并。
先化为最简二次根式
把同类二次根式合并(合并系数)。
课堂小结
16.3 二根次式的加减
第1课时 二次根式的加减
学习目标
1、了解同类二次根式的意义。
2、能熟练进行二次根式的加减运算。
重点
二次根式加减法的运算。
难点
熟练进行二次根式加减法的运算。
问题1 满足什么条件的根式是最简二次根式
问题2 化简下列两组二次根式,每组化简后有什么共同特点
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
化简后被开方数相同
复习引入
合并同类项的过程是通过使用分配律来完成的!
同类项、合并同类项知识点回顾
合并同类项概念:
合并同类项注意事项:
1.合并同类项后,所得项的系数是合并前各同类项的系数的和。
2.合并同类项后,字母连同它的指数不变。
把多项式中的同类项合并成一项,叫做
合并同类项.
练一练:
1. 2x5-6x5+5x5 =
2. 3a2-4a2+a3 =
x5
a3-a2
同类项概念:
所含字母相同,并且相同字母的指数也相
同的项叫做同类项
问题3 有八只小白兔,每只身上都标有一个最简二次根式,你能根据被开方数的特征将这些小白兔分到四个不同的栅栏里吗?
a
a
a
a
a
a
a
a
a
a
=
+
在七年级我们就已经学过单项式加单项式的法则.观察下图并思考.
由上图,易得2a+3a=5a.
当a= 时,分别代入左右得 ;
当a= 时,分别代入左右得 ;
......
讲授新课
在二次根式的加减运算中可以合并的二次根式
一
你发现了什么?
因为 ,两者可以合并为8
当a= ,b= 时,得2a+3b= .
a
2a+3b
b
=
+
b
b
a
自学指导1(3分钟)
问题1 观察下图,并用代数式表达,如果a= ,b= 时,求代数式的值
这两个二次根式可以合并吗?
问题2 通过上面的推导,说出二次根式的合并的一般步骤
①将二次根式化成最简式,
②如果被开方数相同,则这样的二次根式可以合并.
③
注意:判断二次根式能否合并,一定都要化为最简二次根式
练一练
1.下列各式中,与 是同类二次根式的是( )
A. B. C. D.
D
2. 与最简二次根式 能合并,则m=_____.
1
3.下列二次根式,不能与 合并的是________(填
序号).
②⑤
二次根式的加减及其应用
二
思考 现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个分别是8dm2和18dm2的正方形木板?
7.5dm
5dm
问题1 怎样列式求两个正方形边长的和
S=8dm2
S=18dm2
问题2 所列算式能直接进行加减运算吗 如果不能,把式中各个二次根式化成最简二次根式后,再试一试(说出每步运算的依据).
(化成最简二次根式)
(逆用分配律)
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
解:列式如下:
在有理数范围内成立的运算律,在实数范围内仍然成立.
归纳总结
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
典例精析
例2 计算:
解:
例3 计算:
解:
有括号,先去括号
巩固提高
练习1 计算:
(1)
(2)
.
(3)
(4)
1.计算:(1) (2)
(3) (4)
解:
解:
5.计算:
解:
二次根式的加减与整式的加减根据都是分配律,它们的运算实质也基本相同。
二次根式的加减即为对同类二次根式的合并。
先化为最简二次根式
把同类二次根式合并(合并系数)。
课堂小结
