第三章 图形的平移与旋转同步练习题(含答案)
文档属性
| 名称 | 第三章 图形的平移与旋转同步练习题(含答案) | 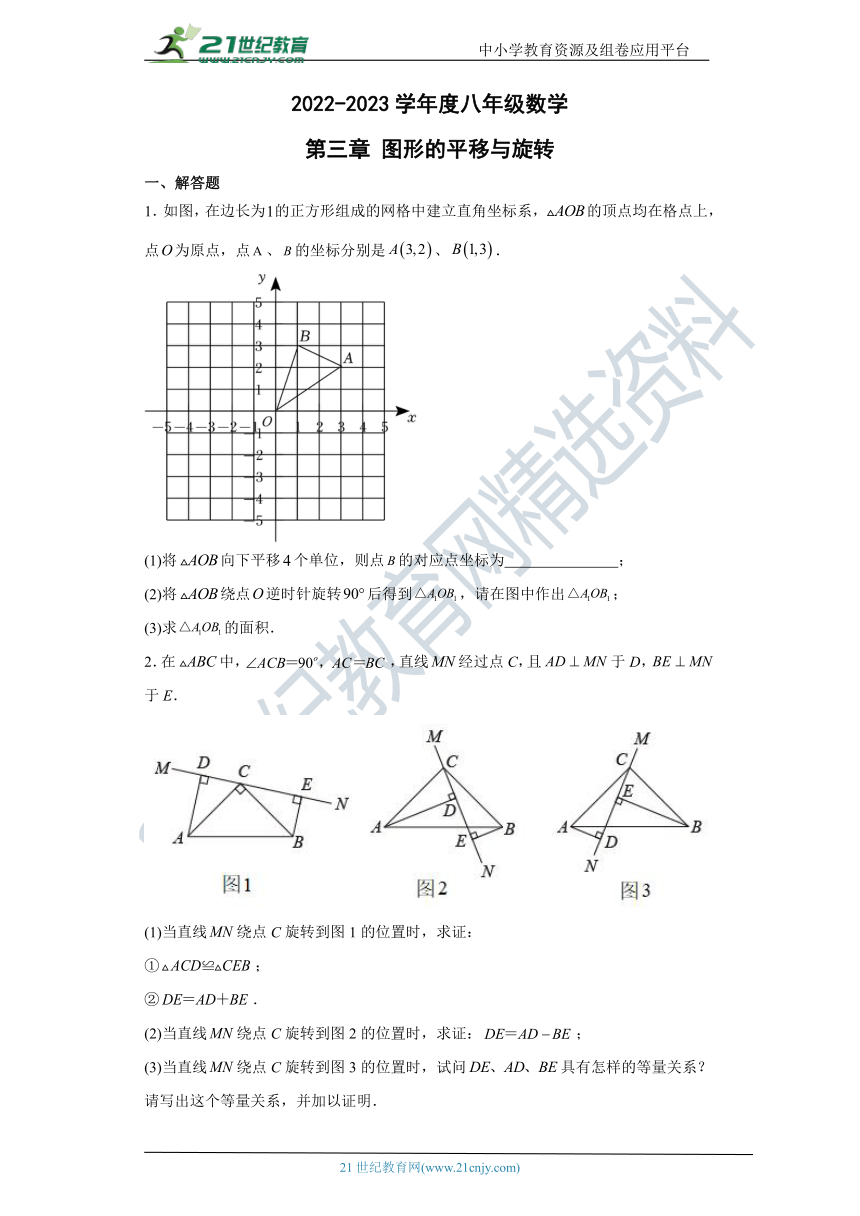 | |
| 格式 | docx | ||
| 文件大小 | 301.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 19:32:48 | ||
图片预览




文档简介
2022-2023学年度八年级数学
第三章 图形的平移与旋转
一、解答题
1.如图,在边长为的正方形组成的网格中建立直角坐标系,的顶点均在格点上,点为原点,点、的坐标分别是、.
(1)将向下平移个单位,则点的对应点坐标为 ;
(2)将绕点逆时针旋转后得到,请在图中作出;
(3)求的面积.
2.在中,,直线经过点C,且于D,于E.
(1)当直线绕点C旋转到图1的位置时,求证:
①;
②.
(2)当直线绕点C旋转到图2的位置时,求证:;
(3)当直线绕点C旋转到图3的位置时,试问具有怎样的等量关系?请写出这个等量关系,并加以证明.
3.如图,点O是等边三角形内一点,,.将 绕点C按顺时针方向旋转60°得到,连结.
(1)求证:是等边三角形.
(2)当时,判断的形状,并说明理由.
(3)当是等腰三角形时,直接写出的度数.
4.如图点O是等边内一点,,∠ACD=∠BCO,OC=CD,
(1)试说明:是等边三角形;
(2)当时,试判断的形状,并说明理由;
(3)当为多少度时,是等腰三角形
5.如图,正方形ABCD内有一点P,若PA=1,PB=2,PC=3.
(1)画出△ABP绕点B顺时针旋转90°得到的△CBE;
(2)求∠APB度数;
(3)求正方形ABCD的面积.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)图见解析;
(2)图见解析
(3)
【分析】(1)利用平移变换的性质作出图形,可得结论;
(2)利用旋转变换的性质作出图形即可;
(3)把三角形的面积看成矩形的面积减去周围的三个三角形面积即可.
【详解】(1)解:如图,即为所求,.
故答案为:.
(2)解:如图,即为所求.
(3)解:.
【点睛】本题考查了图形的平移和旋转的画法,及在网格图中求三角形的面积,确定旋转中心、旋转角度、旋转方向是解答本题的关键.
2.(1)①见解析;②见解析
(2)见解析
(3),证明见解析
【分析】(1)①由垂直关系可得,则由即可证明;
②由的性质及线段和的关系即可证得结论;
(2)由垂直可得,则由可证明,由全等三角形的性质及线段差的关系即可证得结论;
(3)由垂直可得,则由可证得,由全等三角形的性质及线段的和差关系即可得到三线段间的关系.
【详解】(1)解:如图
①∵,
∴,
∴.
又∵,,
∴.
②∵,
∴,,
∴.
(2)∵,
∴,
∴.
又∵,
∴,
∴,
∴.
(3)当旋转到图3的位置时,所满足的等量关系是(或等).
∵,
∴,
∴,
又∵,
∴,
∴,
∴.
【点睛】本题考查了全等三角形的判定与性质,互余的性质等知识,证明两个三角形全等是问题的关键.
3.(1)证明见详解
(2)是直角三角形;理由见详解
(3)110°或125°或140°
【分析】(1)先求出,再由旋转得出,即可得出结论;
(2)先求出 ,再求出,即可得出结论;
(3)先表示出,进而求出,再分三种情况,建立方程求解,即可得出结论.
【详解】(1)∵是等边三角形,
∴,
由旋转,得,
∴,
∴,
∴是等边三角形;
(2)当时,是直角三角形,
理由:由旋转,得,
由(1)知,为等边三角形,
∴,
∴,
∴是直角三角形.
(3)解:由(1)知,为等边三角形,
∴,
∴ ,
,
∴,
∵是等腰三角形,
①当时,即,
解得:;
②当时,则,
解得:;
③当时,即,
解得:;
即α的度数为110°或125°或140°.
【点睛】此题是几何变换综合题,主要考查了等边三角形的判定和性质,旋转的性质,直角三角形的判定,等腰三角形的性质,用分类讨论和方程的思想解决问题是解本题的关键.
4.(1)见解析;(2)△AOD是直角三角形,理由见解析;(3) 110°或125°或140°时,△AOD是等腰三角形.
【分析】(1)根据CO=CD,∠OCD=60°,然后根据等边三角形的判定方法即可得到△COD是等边三角形;
(2)先求得∠ADC=∠BOC=α=150°,再利用△COD是等边三角形得∠CDO=60°,于是可计算出∠ADO=90°,由此可判断△AOD是直角三角形;
(3)先利用α表示出∠ADO=α-60°,∠AOD=190°-α,再进行分类讨论:当∠AOD=∠ADO时,△AOD是等腰三角形,即190°-α=α-60°;当∠AOD=∠DAO时,△AOD是等腰三角形,即2(190°-α)+α-60°=180°;当∠ADO=∠DAO时,△AOD是等腰三角形,即190°-α+2(α-60°)=180°,然后分别解方程求出对应的α的值即可.
【详解】(1)∵∠ACD=∠BCO
∴∠ACD+∠ACO=∠BCO+∠ACO=60°
又∵CO=CD
∴△COD是等边三角形;
(2)∵△COD是等边三角形
∴CO=CD
又∵∠ACD=∠BCO,AC=BC
∴△ACD≌△BCO(SAS)
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠CDO=60°,
∴∠ADO=∠ADC ∠CDO=90°,
∴△AOD是直角三角形;
(3)∵△COD是等边三角形,
∴∠CDO=∠COD=60°,
∴∠ADO=α 60°,∠AOD=360° 60° 110° α=190° α,
当∠AOD=∠ADO时,△AOD是等腰三角形,即190° α=α 60°,解得α=125°;
当∠AOD=∠DAO时,△AOD是等腰三角形,即2(190° α)+α 60°=180°,解得α=140°;
当∠ADO=∠DAO时,△AOD是等腰三角形,即190° α+2(α 60°)=180°,解得α=110°,
综上所述,∠BOC的度数为110°或125°或140°时,△AOD是等腰三角形.
【点睛】此题考查等腰三角形的判定,旋转的性质,等边三角形的判定与性质,解题关键在于掌握判定定理.
5.(1)画图见解析;(2)∠APB=135°;(3)正方形ABCD的面积为5+2.
【分析】(1)作∠QBC=∠ABP,BP=BQ=2,连接QC即可得出△BCQ;
(2)先由△BPQ是等腰直角三角形求出∠BQP的度数,再证明∠PQC=90°,即可得出∠BQC的度数,进而得出结论;
(3)如图,作CH⊥BQ交BQ的延长线于H.求出BH,CH,利用勾股定理即可解决问题.
【详解】(1)作∠QBC=∠ABP,BP=BQ=2,连接QC即可得出△BCQ;
(2)连接PQ,
在Rt△PBQ中∵BP=BQ=2,
∴PQ2=BP2+BQ2=22+22=8,
在△PCQ中,
∵PC=3,QC=AP=1,
∴PC2=PQ2+QC2,
∴△PCQ是直角三角形,∠PQC=90°,
∵BP=BQ=2,∠PBQ=90°,
∴△PBQ是等腰直角三角形,
∴∠BQP=45°,
∵∠PQC=90°,
∴∠BQC=∠BQP+∠PQC=45°+90°=135°,
∵△BQC由△BPA旋转而成,
∴∠APB=∠BQC=135°.
(3)如图,作CH⊥BQ交BQ的延长线于H,
∵∠BQC=135°,
∴∠CQH=∠QCH=45°,
∴CH=QH,∵CQ=QP=1,
∴CH=QH=,
∴BH=BQ+QH=2+,
在Rt△BCH中,BC===,
∴正方形ABCD的面积为5+2.
【点睛】本题考查的是作图-旋转变换、勾股定理的逆定理及正方形的性质,熟知图形经过旋转后所得图形与原图形全等是解答此题的关键.
第三章 图形的平移与旋转
一、解答题
1.如图,在边长为的正方形组成的网格中建立直角坐标系,的顶点均在格点上,点为原点,点、的坐标分别是、.
(1)将向下平移个单位,则点的对应点坐标为 ;
(2)将绕点逆时针旋转后得到,请在图中作出;
(3)求的面积.
2.在中,,直线经过点C,且于D,于E.
(1)当直线绕点C旋转到图1的位置时,求证:
①;
②.
(2)当直线绕点C旋转到图2的位置时,求证:;
(3)当直线绕点C旋转到图3的位置时,试问具有怎样的等量关系?请写出这个等量关系,并加以证明.
3.如图,点O是等边三角形内一点,,.将 绕点C按顺时针方向旋转60°得到,连结.
(1)求证:是等边三角形.
(2)当时,判断的形状,并说明理由.
(3)当是等腰三角形时,直接写出的度数.
4.如图点O是等边内一点,,∠ACD=∠BCO,OC=CD,
(1)试说明:是等边三角形;
(2)当时,试判断的形状,并说明理由;
(3)当为多少度时,是等腰三角形
5.如图,正方形ABCD内有一点P,若PA=1,PB=2,PC=3.
(1)画出△ABP绕点B顺时针旋转90°得到的△CBE;
(2)求∠APB度数;
(3)求正方形ABCD的面积.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)图见解析;
(2)图见解析
(3)
【分析】(1)利用平移变换的性质作出图形,可得结论;
(2)利用旋转变换的性质作出图形即可;
(3)把三角形的面积看成矩形的面积减去周围的三个三角形面积即可.
【详解】(1)解:如图,即为所求,.
故答案为:.
(2)解:如图,即为所求.
(3)解:.
【点睛】本题考查了图形的平移和旋转的画法,及在网格图中求三角形的面积,确定旋转中心、旋转角度、旋转方向是解答本题的关键.
2.(1)①见解析;②见解析
(2)见解析
(3),证明见解析
【分析】(1)①由垂直关系可得,则由即可证明;
②由的性质及线段和的关系即可证得结论;
(2)由垂直可得,则由可证明,由全等三角形的性质及线段差的关系即可证得结论;
(3)由垂直可得,则由可证得,由全等三角形的性质及线段的和差关系即可得到三线段间的关系.
【详解】(1)解:如图
①∵,
∴,
∴.
又∵,,
∴.
②∵,
∴,,
∴.
(2)∵,
∴,
∴.
又∵,
∴,
∴,
∴.
(3)当旋转到图3的位置时,所满足的等量关系是(或等).
∵,
∴,
∴,
又∵,
∴,
∴,
∴.
【点睛】本题考查了全等三角形的判定与性质,互余的性质等知识,证明两个三角形全等是问题的关键.
3.(1)证明见详解
(2)是直角三角形;理由见详解
(3)110°或125°或140°
【分析】(1)先求出,再由旋转得出,即可得出结论;
(2)先求出 ,再求出,即可得出结论;
(3)先表示出,进而求出,再分三种情况,建立方程求解,即可得出结论.
【详解】(1)∵是等边三角形,
∴,
由旋转,得,
∴,
∴,
∴是等边三角形;
(2)当时,是直角三角形,
理由:由旋转,得,
由(1)知,为等边三角形,
∴,
∴,
∴是直角三角形.
(3)解:由(1)知,为等边三角形,
∴,
∴ ,
,
∴,
∵是等腰三角形,
①当时,即,
解得:;
②当时,则,
解得:;
③当时,即,
解得:;
即α的度数为110°或125°或140°.
【点睛】此题是几何变换综合题,主要考查了等边三角形的判定和性质,旋转的性质,直角三角形的判定,等腰三角形的性质,用分类讨论和方程的思想解决问题是解本题的关键.
4.(1)见解析;(2)△AOD是直角三角形,理由见解析;(3) 110°或125°或140°时,△AOD是等腰三角形.
【分析】(1)根据CO=CD,∠OCD=60°,然后根据等边三角形的判定方法即可得到△COD是等边三角形;
(2)先求得∠ADC=∠BOC=α=150°,再利用△COD是等边三角形得∠CDO=60°,于是可计算出∠ADO=90°,由此可判断△AOD是直角三角形;
(3)先利用α表示出∠ADO=α-60°,∠AOD=190°-α,再进行分类讨论:当∠AOD=∠ADO时,△AOD是等腰三角形,即190°-α=α-60°;当∠AOD=∠DAO时,△AOD是等腰三角形,即2(190°-α)+α-60°=180°;当∠ADO=∠DAO时,△AOD是等腰三角形,即190°-α+2(α-60°)=180°,然后分别解方程求出对应的α的值即可.
【详解】(1)∵∠ACD=∠BCO
∴∠ACD+∠ACO=∠BCO+∠ACO=60°
又∵CO=CD
∴△COD是等边三角形;
(2)∵△COD是等边三角形
∴CO=CD
又∵∠ACD=∠BCO,AC=BC
∴△ACD≌△BCO(SAS)
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠CDO=60°,
∴∠ADO=∠ADC ∠CDO=90°,
∴△AOD是直角三角形;
(3)∵△COD是等边三角形,
∴∠CDO=∠COD=60°,
∴∠ADO=α 60°,∠AOD=360° 60° 110° α=190° α,
当∠AOD=∠ADO时,△AOD是等腰三角形,即190° α=α 60°,解得α=125°;
当∠AOD=∠DAO时,△AOD是等腰三角形,即2(190° α)+α 60°=180°,解得α=140°;
当∠ADO=∠DAO时,△AOD是等腰三角形,即190° α+2(α 60°)=180°,解得α=110°,
综上所述,∠BOC的度数为110°或125°或140°时,△AOD是等腰三角形.
【点睛】此题考查等腰三角形的判定,旋转的性质,等边三角形的判定与性质,解题关键在于掌握判定定理.
5.(1)画图见解析;(2)∠APB=135°;(3)正方形ABCD的面积为5+2.
【分析】(1)作∠QBC=∠ABP,BP=BQ=2,连接QC即可得出△BCQ;
(2)先由△BPQ是等腰直角三角形求出∠BQP的度数,再证明∠PQC=90°,即可得出∠BQC的度数,进而得出结论;
(3)如图,作CH⊥BQ交BQ的延长线于H.求出BH,CH,利用勾股定理即可解决问题.
【详解】(1)作∠QBC=∠ABP,BP=BQ=2,连接QC即可得出△BCQ;
(2)连接PQ,
在Rt△PBQ中∵BP=BQ=2,
∴PQ2=BP2+BQ2=22+22=8,
在△PCQ中,
∵PC=3,QC=AP=1,
∴PC2=PQ2+QC2,
∴△PCQ是直角三角形,∠PQC=90°,
∵BP=BQ=2,∠PBQ=90°,
∴△PBQ是等腰直角三角形,
∴∠BQP=45°,
∵∠PQC=90°,
∴∠BQC=∠BQP+∠PQC=45°+90°=135°,
∵△BQC由△BPA旋转而成,
∴∠APB=∠BQC=135°.
(3)如图,作CH⊥BQ交BQ的延长线于H,
∵∠BQC=135°,
∴∠CQH=∠QCH=45°,
∴CH=QH,∵CQ=QP=1,
∴CH=QH=,
∴BH=BQ+QH=2+,
在Rt△BCH中,BC===,
∴正方形ABCD的面积为5+2.
【点睛】本题考查的是作图-旋转变换、勾股定理的逆定理及正方形的性质,熟知图形经过旋转后所得图形与原图形全等是解答此题的关键.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
