【解析版】辽宁省沈阳市2014届高三教学质量监测(一)数学(理)试题
文档属性
| 名称 | 【解析版】辽宁省沈阳市2014届高三教学质量监测(一)数学(理)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 558.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-06 00:00:00 | ||
图片预览




文档简介
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.设全集,集合,,则( )
A. B. C. D.
2.若复数满足,则的虚部为( )
A. B.- C.4 D.-4
3.设向量,,若满足,则( )
A. B. C. D.
【答案】D
【解析】
试题分析:因为,所以, ,解得: ,故选D.
考点:向量共线的条件.
4.已知,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
5.在等比数列中,若,是方程的两根,则的值是 ( )
A. B. C. D.
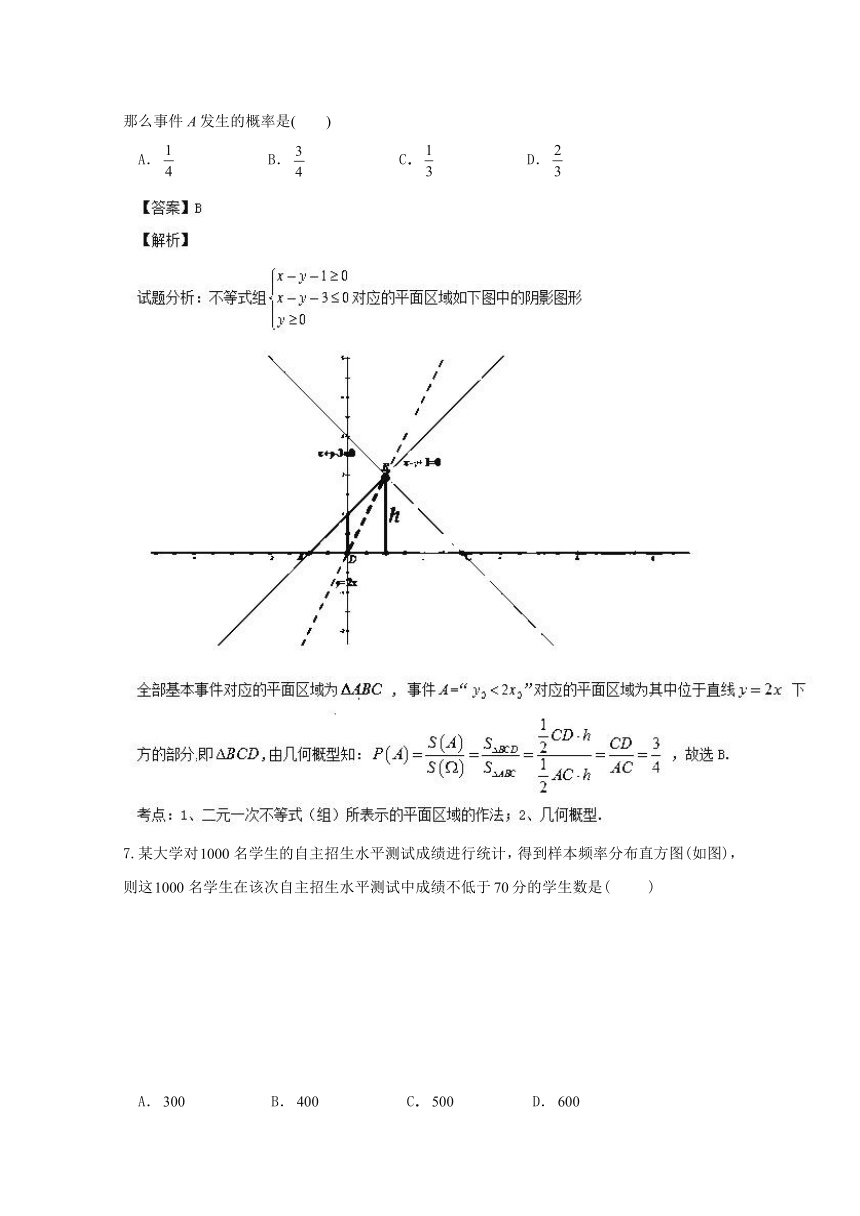
6.在满足不等式组的平面点集中随机取一点,设事件=“”,
那么事件发生的概率是( )
A. B. C. D.
7.某大学对名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图(如图),则这名学生在该次自主招生水平测试中成绩不低于分的学生数是( )
A. B. C. D.
8.已知双曲线的一个焦点与抛物线的焦点重合,则此双曲线的离心率为( )
A.2 B. C.3 D.4
9.有如图所示的程序框图,则该程序框图表示的算法的功能是( )
A.输出使成立的最小整数.
B.输出使成立的最大整数.
C.输出使成立的最大整数+2.
D.输出使成立的最小整数+2.
10.已知直线()经过圆的圆心,则的最小值是( )
A.9 B.8 C.4 D.2
11.已知四面体的四个顶点都在球的球面上,若平面,,且,
,则球的表面积为( )
A. B. C. D.
12.已知函数是R上的可导函数,当时,有,则函数的零点个数是( )
A.0 B.1 C.2 D.3
第Ⅱ卷(共90分)
二、填空题(本大题共4小题,每小题5分,共20分,将答案填在答题纸上)
13.某一容器的三视图如图所示,则该几何体的体积为__________.
14.已知的三个内角所对的边分别为,
且,则角的大小为 .
15.定义运算:,例如:,,
则函数的最大值为____________.
16.已知为定义在上的偶函数,当时,有,且当时,,给出下列命题:
①的值为0;②函数在定义域上为周期是2的周期函数;
③直线与函数的图像有1个交点;④函数的值域为.
其中正确的命题序号有 .
【答案】①③④
【解析】
试题分析:根据题意,可在同一坐标系中画出直线和函数的图象如下:
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分12分)已知函数,记函数的最小正周期为,
向量, (),且.
(Ⅰ)求在区间上的最值;
(Ⅱ)求的值.
(Ⅱ) ……………………………………………………………………7分
……………………………………………………………………9分
====…………………………12分
(此处涉及三个三角公式,请各位阅卷老师酌情处理)
考点:1、同角三角函数的基本关系;2、两角和与差的正弦公式、二倍角公式;3、三角函数的性质.
18.(本小题满分12分)某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
围棋社
舞蹈社
拳击社
男生
5
10
28
女生
15
30
m
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从三个社团成员中抽取18人,结果拳击社被抽出了6人.
(Ⅰ)求拳击社团被抽出的6人中有5人是男生的概率;
(Ⅱ)设拳击社团有X名女生被抽出,求X的分布列及数学期望.
19.(本小题满分12分)四棱锥,底面为平行四边形,
侧面底面.已知,,
,为线段的中点.
(Ⅰ)求证:平面;
(Ⅱ)求面与面所成二面角大小.
20.(本小题满分12分)已知函数,.
(Ⅰ)若与在处相切,试求的表达式;
(Ⅱ)若在上是减函数,求实数的取值范围;
(Ⅲ)证明不等式:.
当时: 即
21.(本小题满分12分)已知两点,直线AM、BM相交于点M,且这两条直线的斜率之积为.
(Ⅰ)求点M的轨迹方程;
(Ⅱ)记点M的轨迹为曲线C,曲线C上在第一象限的点P的横坐标为1,直线PE、PF与圆()相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
求△OQR的面积的最大值(其中点O为坐标原点).
试题解析:(Ⅰ)设点, …………………………2分
所以 ………………………………10分
原点O到直线RQ的距离为 ………………………………………………11分
………………12分
考点:1、动点轨迹方程的求法;2、直线与圆、圆锥曲线的位置关系;3、基本不等式的应用.
22.(本小题满分10分)选修4—1:几何证明选讲
如图,已知圆与圆外切于点,直线是两圆的外公切线,分别与两圆相切于两点,是圆的直径,过作圆的切线,切点为.
(Ⅰ)求证:三点共线;
(Ⅱ)求证:.
23.(本小题满分10分)选修4—4:极坐标与参数方程
已知曲线的极坐标方程为,曲线的极坐标方程为,曲线、相交于、两点. ( )
(Ⅰ)求、两点的极坐标;
(Ⅱ)曲线与直线(为参数)分别相交于两点,求线段的长度.
24.(本小题满分10分)选修4—5:不等式选讲
已知函数.
(Ⅰ)若,使得不等式成立,求的取值范围;
(Ⅱ)求使得等式成立的的取值范围.
同课章节目录
