《名师学典·数学》学案:新人教八下18.2.2菱形的判定例题+中考题训练+课时自测(答案详细)
文档属性
| 名称 | 《名师学典·数学》学案:新人教八下18.2.2菱形的判定例题+中考题训练+课时自测(答案详细) |  | |
| 格式 | zip | ||
| 文件大小 | 329.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-07 11:16:16 | ||
图片预览

文档简介
《名题学典·数学》人教版八年级系列第十八章
18.2.2 菱形的判定
1.回顾:
菱形的定义:
菱形的性质:
菱形的面积公式:
2.判定菱形的两个定理:
3.请写出判定菱形的两种思路:
4.(1)请判断下列哪些条件能判定四边形ABCD是菱形的有 .
①AC⊥BD,AC与BD互相平分
②AB=BC=CD=DA
③AB=BC,AD=CD,AC⊥BD
④AB=CD,AD=BC,AC⊥BD
(2)请判断下列哪些条件能判定□ABCD是菱形的有 .
①AC⊥BD
②∠BAD=90°
③AB=BC
④AC=BD
用菱形的定义判定
学会运用菱形的定义判定菱形.
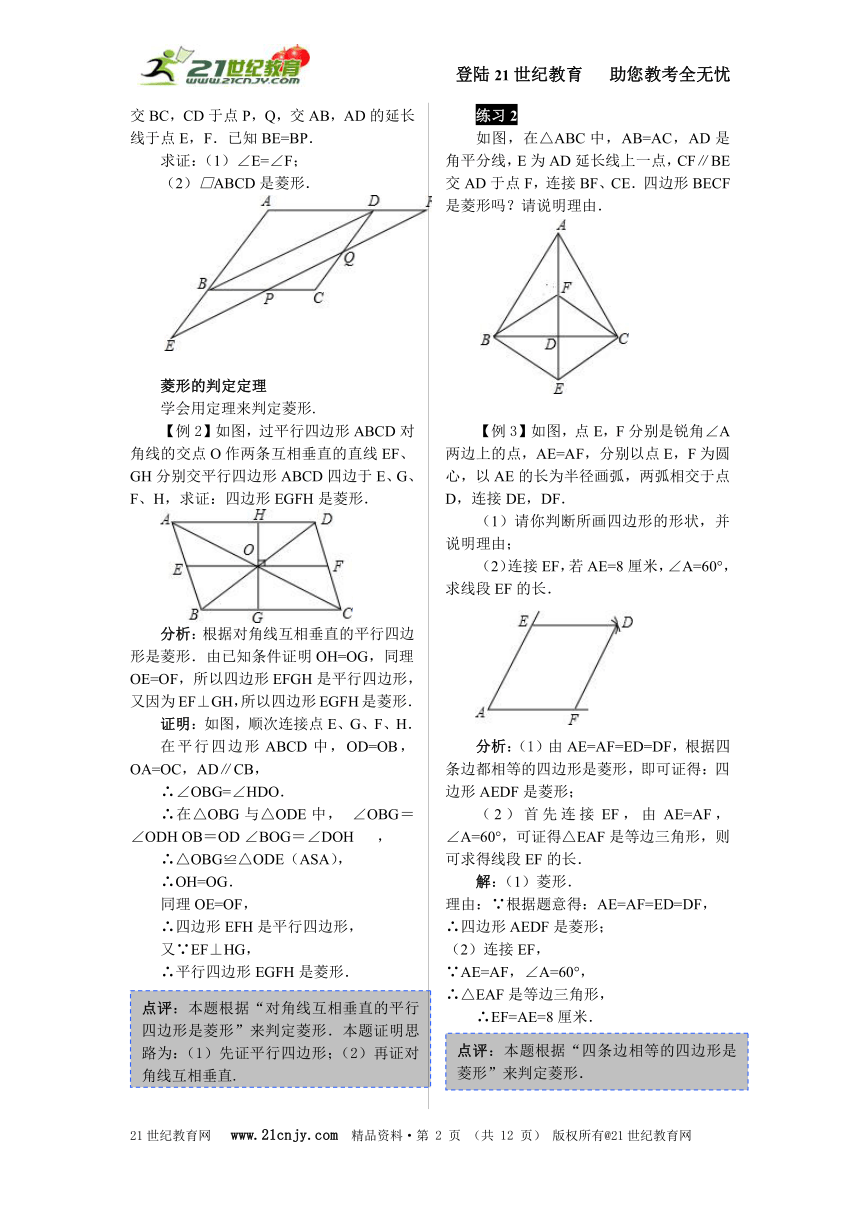
【例1】如图,四边形ABCD为平行四边形,BD为对角线,点E在AB边的延长线上,作EF∥BD,交BC边于点F,BE=BF.求证:四边形ABCD是菱形.
分析:根据平行线性质和等腰三角形性质推出∠DBC=∠DBA,推出DC=BC,根据菱形的判定推出即可.
证明:∵EF∥BD,
∴∠E=∠ABD,∠EFB=∠DBC,
∵BE=BF,
∴∠E=∠EFB,
∴∠DBC=∠DBA,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CDB=∠DBA,
∴∠CDB=∠CBD,
∴DC=BC,
∴平行四边形ABCD是菱形.
练习1
如图,在□ABCD中,EF∥BD,分别交BC,CD于点P,Q,交AB,AD的延长线于点E,F.已知BE=BP.
求证:(1)∠E=∠F;
(2)□ABCD是菱形.
菱形的判定定理
学会用定理来判定菱形.
【例2】如图,过平行四边形ABCD对角线的交点O作两条互相垂直的直线EF、GH分别交平行四边形ABCD四边于E、G、F、H,求证:四边形EGFH是菱形.
分析:根据对角线互相垂直的平行四边形是菱形.由已知条件证明OH=OG,同理OE=OF,所以四边形EFGH是平行四边形,又因为EF⊥GH,所以四边形EGFH是菱形.
证明:如图,顺次连接点E、G、F、H.
在平行四边形ABCD中,OD=OB,OA=OC,AD∥CB,
∴∠OBG=∠HDO.
∴在△OBG与△ODE中, ∠OBG=∠ODH OB=OD ∠BOG=∠DOH ,
∴△OBG≌△ODE(ASA),
∴OH=OG.
同理OE=OF,
∴四边形EFH是平行四边形,
又∵EF⊥HG,
∴平行四边形EGFH是菱形.
练习2
如图,在△ABC中,AB=AC,AD是角平分线,E为AD延长线上一点,CF∥BE交AD于点F,连接BF、CE.四边形BECF是菱形吗?请说明理由.
【例3】如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
(1)请你判断所画四边形的形状,并说明理由;
(2)连接EF,若AE=8厘米,∠A=60°,求线段EF的长.
分析:(1)由AE=AF=ED=DF,根据四条边都相等的四边形是菱形,即可证得:四边形AEDF是菱形;
(2)首先连接EF,由AE=AF,∠A=60°,可证得△EAF是等边三角形,则可求得线段EF的长.
解:(1)菱形.
理由:∵根据题意得:AE=AF=ED=DF,
∴四边形AEDF是菱形;
(2)连接EF,
∵AE=AF,∠A=60°,
∴△EAF是等边三角形,
∴EF=AE=8厘米.
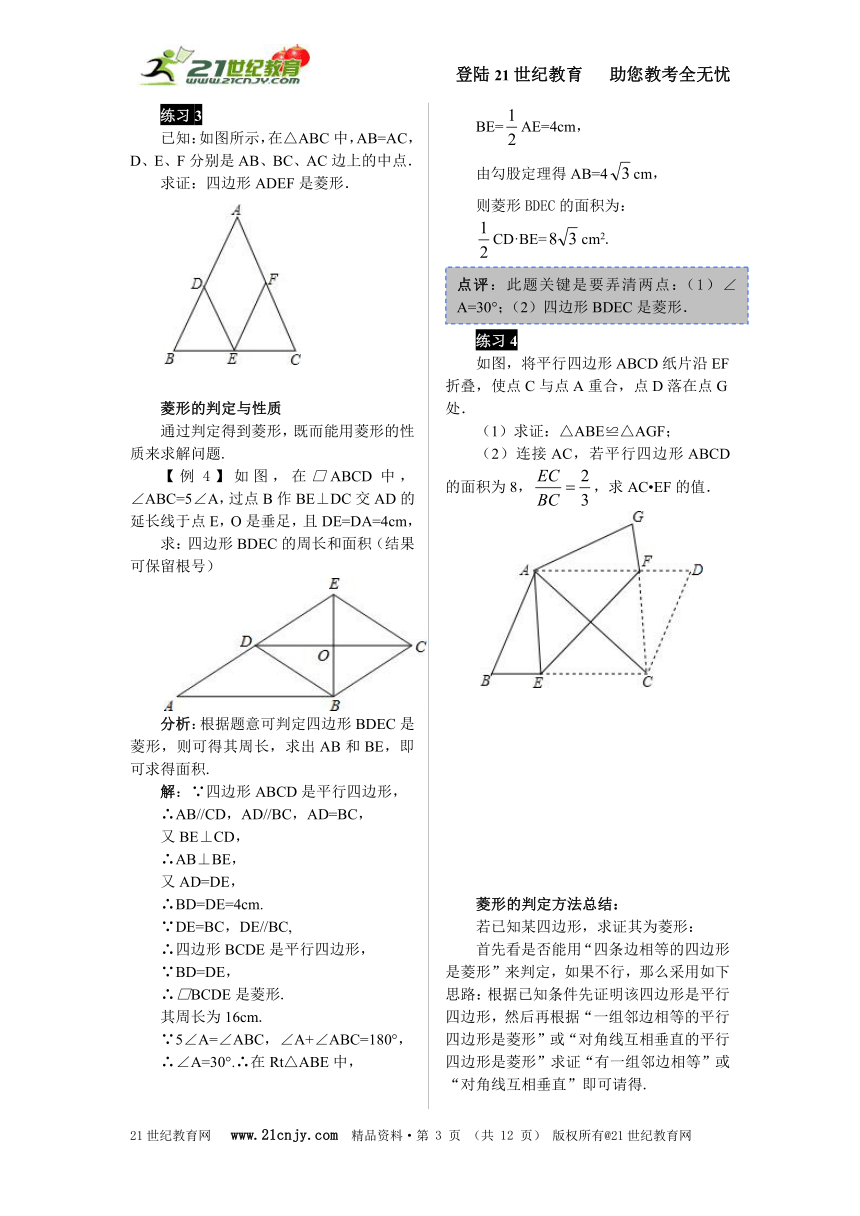
练习3
已知:如图所示,在△ABC中,AB=AC,D、E、F分别是AB、BC、AC边上的中点.
求证:四边形ADEF是菱形.
菱形的判定与性质
通过判定得到菱形,既而能用菱形的性质来求解问题.
【例4】如图,在□ABCD中,∠ABC=5∠A,过点B作BE⊥DC交AD的延长线于点E,O是垂足,且DE=DA=4cm,
求:四边形BDEC的周长和面积(结果可保留根号)
分析:根据题意可判定四边形BDEC是菱形,则可得其周长,求出AB和BE,即可求得面积.
解:∵四边形ABCD是平行四边形,
∴AB//CD,AD//BC,AD=BC,
又BE⊥CD,
∴AB⊥BE,
又AD=DE,
∴BD=DE=4cm.
∵DE=BC,DE//BC,
∴四边形BCDE是平行四边形,
∵BD=DE,
∴□BCDE是菱形.
其周长为16cm.
∵5∠A=∠ABC,∠A+∠ABC=180°,
∴∠A=30°.∴在Rt△ABE中,
BE=AE=4cm,
由勾股定理得AB=4cm,
则菱形BDEC的面积为:
CD·BE=cm2.
练习4
如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处.
(1)求证:△ABE≌△AGF;
(2)连接AC,若平行四边形ABCD的面积为8,,求AC?EF的值.
菱形的判定方法总结:
若已知某四边形,求证其为菱形:
首先看是否能用“四条边相等的四边形是菱形”来判定,如果不行,那么采用如下思路:根据已知条件先证明该四边形是平行四边形,然后再根据“一组邻边相等的平行四边形是菱形”或“对角线互相垂直的平行四边形是菱形”求证“有一组邻边相等”或“对角线互相垂直”即可请得.
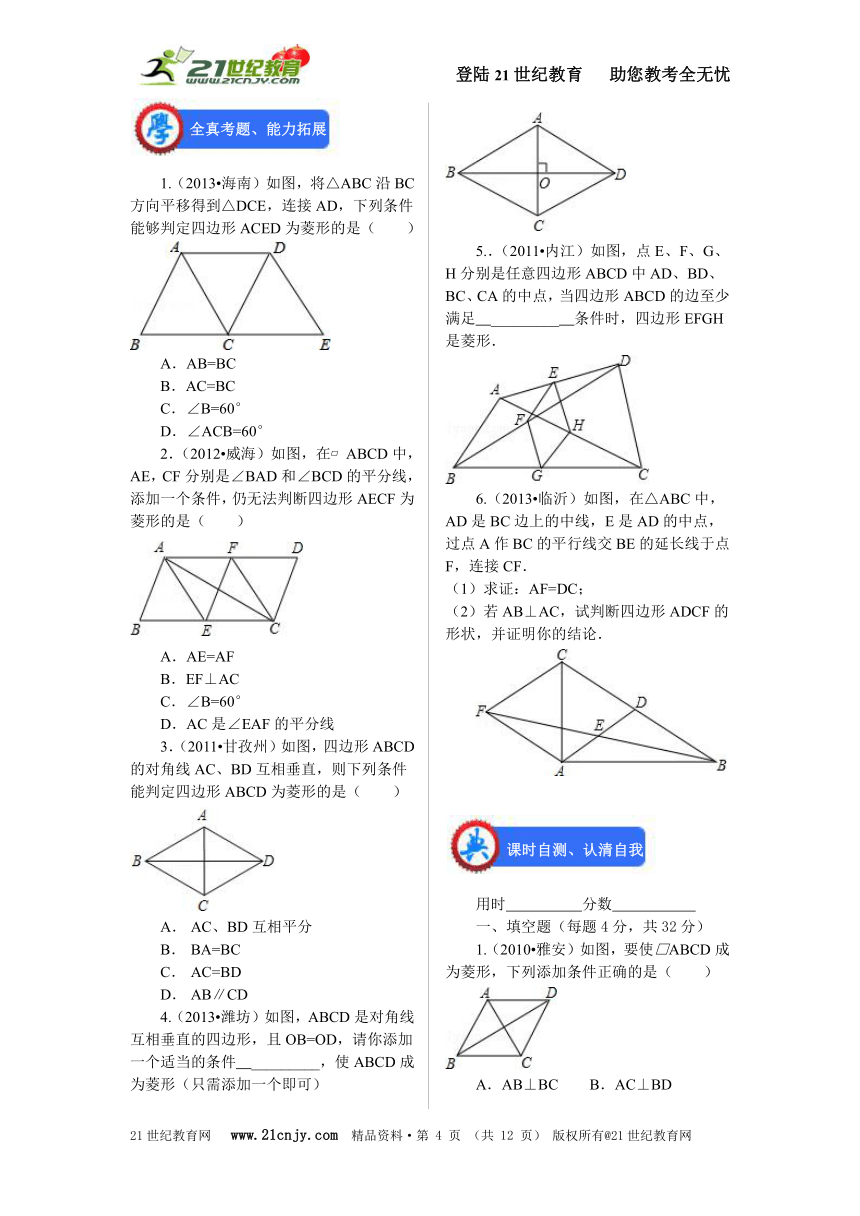
1.(2013?海南)如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )
A.AB=BC
B.AC=BC
C.∠B=60°
D.∠ACB=60°
2.(2012?威海)如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AECF为菱形的是( )
A.AE=AF
B.EF⊥AC
C.∠B=60°
D.AC是∠EAF的平分线
3.(2011?甘孜州)如图,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A. AC、BD互相平分
B. BA=BC
C. AC=BD
D. AB∥CD
4.(2013?潍坊)如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 _________,使ABCD成为菱形(只需添加一个即可)
5..(2011?内江)如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足 _________ 条件时,四边形EFGH是菱形.
6.(2013?临沂)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
用时 分数
一、填空题(每题4分,共32分)
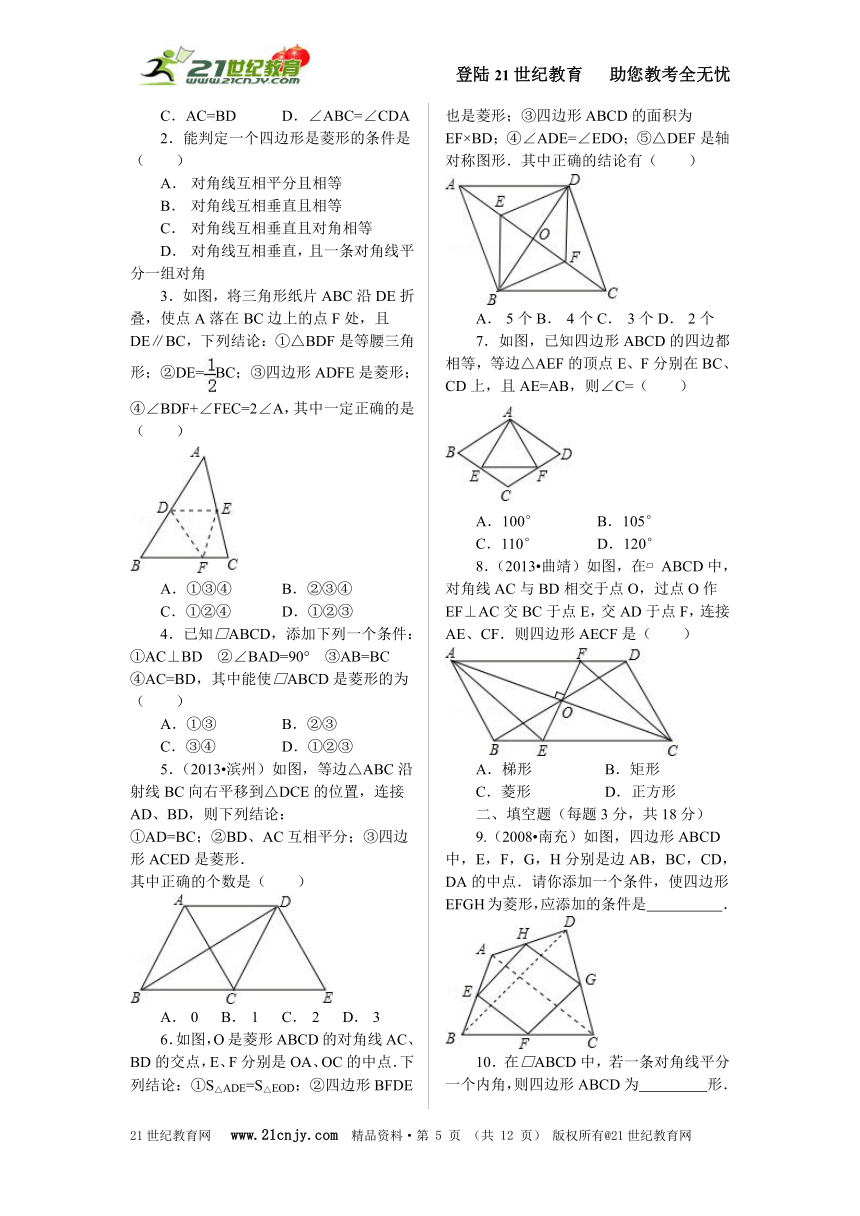
1.(2010?雅安)如图,要使□ABCD成为菱形,下列添加条件正确的是( )
A.AB⊥BC B.AC⊥BD
C.AC=BD D.∠ABC=∠CDA
2.能判定一个四边形是菱形的条件是( )
A. 对角线互相平分且相等
B. 对角线互相垂直且相等
C. 对角线互相垂直且对角相等
D. 对角线互相垂直,且一条对角线平分一组对角
3.如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论:①△BDF是等腰三角形;②DE=BC;③四边形ADFE是菱形;④∠BDF+∠FEC=2∠A,其中一定正确的是( )
A.①③④ B.②③④
C.①②④ D.①②③
4.已知□ABCD,添加下列一个条件:①AC⊥BD ②∠BAD=90° ③AB=BC ④AC=BD,其中能使□ABCD是菱形的为( )
A.①③ B.②③
C.③④ D.①②③
5.(2013?滨州)如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:
①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.
其中正确的个数是( )
A. 0 B. 1 C. 2 D. 3
6.如图,O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③四边形ABCD的面积为EF×BD;④∠ADE=∠EDO;⑤△DEF是轴对称图形.其中正确的结论有( )
A. 5个 B. 4个 C. 3个 D. 2个
7.如图,已知四边形ABCD的四边都相等,等边△AEF的顶点E、F分别在BC、CD上,且AE=AB,则∠C=( )
A.100° B.105°
C.110° D.120°
8.(2013?曲靖)如图,在?ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF.则四边形AECF是( )
A.梯形 B.矩形
C.菱形 D.正方形
二、填空题(每题3分,共18分)
9.(2008?南充)如图,四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点.请你添加一个条件,使四边形EFGH为菱形,应添加的条件是 .
10.在□ABCD中,若一条对角线平分
一个内角,则四边形ABCD为 形.
11.四边形的四条边长分别为a,b,c,d,满足条件a2+b2+c2=ab+bc+cd+da,则此四边形一定是 ______ .
12.如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF.
(1)四边形ADEF是 _________ ;
(2)当△ABC满足条件 _________ 时,四边形ADEF为菱形;
(3)当△ABC满足条件 _________ 时,四边形ADEF不存在.
13.如图,两张宽度均为3cm的纸条交错叠放在一起,相交成锐角α,且两张纸片中重叠部分的面积为9cm2,则锐角α的度数 _________ .
14.已知如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB,交CB的延长线于G,连接GF,若AD⊥BD.下列结论:
①DE∥BF;②四边形BEDF是菱形;③FG⊥AB;④S△BFG=S四边形ABCD
其中正确的是 _________ .
三、解答题(共40分)
15.(6分)(2002?咸宁)如图所示,已
知AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,
求证:AD⊥EF.
16.(6分)(2013?遂宁)如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是E、F,并且DE=DF.求证:
(1)△ADE≌△CDF;
(2)四边形ABCD是菱形.
17.(6分)(2013?盐城)如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD且AE=AB.
(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.
21世纪教育网版权所有
18.(6分)(2010?沈阳)如图,菱形ABCD的对角线AC与BD相交于点O,点E,F分别为边AB,AD的中点,连接EF,OE,OF,求证:四边形AEOF是菱形.
21世纪教育网版权所有
19.(8分)(2013?安顺)如图,在△ABC中,
D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
20.(8分)(2012?建宁县质检)如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形;
(3)在(2)的条件下,若AB=AO,且OD=a,求菱形ADCE的周长.
21世纪教育网版权所有
21世纪教育网版权所有
参考答案
基础为本、掌握新知
1.有一组邻边相等的平行四边形是菱形.
(1)边:四条边相等;两组对边平行且相等;
(2)角:两组对角相等;邻角互补;
(3)对角线:对角线互相平分且垂直;每一条对角线平分一组对角.
两条对角线之积的一半
2.有四条边相等的四边形是菱形;对角线互相垂直的平行四边形是菱形
3.(1)由四边形,证四条边相等,得菱形;(2)由四边形,先请其为平行四边形,再证其为菱形.
4.(1)①②④ (2)①③
一例一练、活用数学
练习1 证明:(1)∵BE=BP,∴∠E=∠BPE,∵BC∥AF,∴∠BPE=∠F,∴∠E=∠F. (2)∵EF∥BD,∴∠E=∠ABD,∠F=∠ADB,∴∠ABD=∠ADB,
∴AB=AD,∵四边形ABCD是平行四边形,∴□ABCD是菱形.
练习2 证明:∵AB=AC,AD是角平分线,∴BD=CD,∵CF∥BE,∴∠DBE=∠FCD,在△CDF和△BDE中,∠DBE=∠FCD,DB=CD,∠BDE=∠CDF,
∴△BDE≌△CDF(ASA),∴CF=BE,又∵CF∥BE,∴四边形BFCE是平行四边形;
∵AB=AC,D是BC的中点,∴AD⊥BC,又∵四边形BFCE是平行四边形,
∴四边形BFCE是菱形.
(2)解:连接CF,∵△ABE≌△AGF,∴AE=AF,根据翻折的性质EC=AE,∴EC=AE=AF,又∵AF∥EC,∴四边形AECF是平行四边形,根据翻折后点A、C重合,∴AC⊥EF,
∴□AECF是菱形,∴AC?EF=2×菱形AECF的面积,
∵□ABCD的面积=8,,∴△AEC的面积=×8×=,
∴菱形AECF的面积等于,∴AC?EF=2×菱形AECF的面积=.
全真考题、能力拓展
1.B 【解析】∵将△ABC沿BC方向平移得到△DCE,∴ABCD,∴四边形ABCD为平行四边形,当AC=BC时,平行四边形ACED是菱形.
2.C
3.A 【解析】A、∵AC、BD互相平分,∴四边形ABCD是平行四边形,
∵AC⊥BD(已知),∴平行四边形ABCD是菱形,故本选项正确;B、根据已知AC⊥BD和BA=BC不能推出四边形ABCD是平行四边形,即更不是菱形,故本选项错误;
C、根据已知AC⊥BD和AC=BD不能推出四边形ABCD是平行四边形,即更不是菱形,故本选项错误;D、根据已知AC⊥BD和AB∥DC不能推出四边形ABCD是平行四边形,即更不是菱形,故本选项错误.
4.OA=OC(答案不唯一)
(2)四边形ADCF是菱形,证明:AF∥BC,AF=DC,∴四边形ADCF是平行四边形,
∵AC⊥AB,AD是斜边BC的中线,∴AD=DC,∴平行四边形ADCF是菱形.
课时自测、认清自我
1.B 【解析】A、添加AB⊥BC,可以证明?ABCD是矩形,故此选项错误;
B、添加AC⊥BD,可以证明?ABCD是菱形,故此选项正确;
C、添加AC=BD,可以证明?ABCD是矩形,故此选项错误;
D、添加∠ABC=∠CDA不能证明?ABCD是菱形形,故此选项错误;
故选:B.
2.C 【解析】∵对角线互相垂直平分的四边形是菱形.∴A、B、D都不正确.
∵对角相等的四边形是平行四边形,而对角线互相垂直的平行四边形是菱形.
3.C 【解析】分别过点D、E作BC的垂线DG、EH;连接AF,∵折叠是轴对称图形,∴AF⊥DE,∵DE∥BC,∴AF⊥BC,且AM=MF,∴D、E分别是AB、AC的中点,
即;②DE=BC,正确.∵AD=DF,AE=EF,∴DA=DB=DF,∴①△BDF是等腰三角形,正确.∵DG∥AF∥EH,∴∠BDG=∠DAM,又∵DG是等腰三角形BDF的高,
∴∠BDF=2∠DAM,同理∠CEF=2∠EAM,∴④∠BDF+∠FEC=2∠A;如图显然③四边形ADFE是菱形是错误的.故选C.
4.A 【解析】∵四边形ABCD是平行四边形,①若AC⊥BD,则可得其为菱形,故①选项正确,②中∠BAD=90°,得到一矩形,不是菱形,所以②错误,③中一组邻边相等,也可得到一菱形,所以③成立,④中并不能得到其为矩形,菱形或正方形等,所以④不成立,
故A选项中①③都正确,B中②不成立,C中④错误,而D中多一个选项②也不对,
则能使□ABCD是菱形的有①或③.
5.D 【解析】△ABC、△DCE是等边三角形,∴∠ACB=∠DCE=60°,AC=CD,
∴∠ACD=180°﹣∠ACB﹣∠DCE=60°,∴△ACD是等边三角形,∴AD=AC=BC,故①正确;由①可得AD=BC,∵AB=CD,∴四边形ABCD是平行四边形,∴BD、AC互相平分,故②正确;由①可得AD=AC=CE=DE,故四边形ACED是菱形,即③正确.
6.B 【解析】①正确:∵E、F分别是OA、OC的中点.∴AE=OE.∵S△ADE=×AE×OD=×OE×OD=S△EOD∴S△ADE=S△EOD.②正确:∵四边形ABCD是菱形,E,F分别是OA,OC的中点.∴EF⊥OD,OE=OF.∵OD=OD.∴DE=DF.同理:BE=BF∴四边形BFDE是菱形.③正确:∵菱形ABCD的面积=AC×BD.∵E、F分别是OA、OC的中点.∴EF=AC.∴菱形ABCD的面积=EF×BD.④不正确:由已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO.⑤正确:∵EF⊥OD,OE=OF,OD=OD.
∴△DEO≌△DFO.∴△DEF是轴对称图形.∴正确的结论有四个,分别是①②③⑤.
7.A 【解析】∵四边形ABCD的四边都相等,∴四边形ABCD是菱形,∴∠B=∠D,∠A=∠C,AD∥BC,∴∠DAB+∠B=180°,∵△AEF是等边三角形,AE=AB,∴∠AEF=∠AFE=60°,AF=AD,∴∠B=∠AEB,∠D=∠AFD,由三角形的内角和定理得:∠BAE=∠FAD,设∠BAE=∠FAD=x,则∠D=∠AFD=180°﹣60°﹣2x,∵∠FAD+∠D+∠AFD=180°,
∴x+2(180°﹣60°﹣2x)=180°,解得:x=20°,∴∠C=∠BAD=2×20°+60°=100°,故选A.
8.C 【解析】四边形AECF是菱形,理由:∵在□ABCD中,对角线AC与BD相交于点O,∴AO=CO,∠AFO=∠CEO,∴在△AFO和△CEO中
,∴△AFO≌△CEO(AAS),∴FO=EO,∴四边形AECF平行四边形,
∵EF⊥AC,∴平行四边形AECF是菱形.
9.AC=BD(答案不唯一)
10.菱形 【解析】一条对角线平分一个内角,根据两直线平行内错角相等,等角对等边可求得此对角线和一组邻边组成的是等腰三角形,有一组邻边相等的平行四边形是菱形.故四边形ABCD是菱形.
11.菱形 【解析】∵a2+b2+c2+d2=ab+bc+cd+da∴2(a2+b2+c2+d2)﹣2ab﹣2bc﹣2cd﹣2da=0
∴(a﹣b)2+(b﹣c)2+(c﹣d)2+(d﹣a)2=0由非负数的性质可知:(a﹣b)=0,(b﹣c)=0,(c﹣d)=0,(a﹣d)=0,∴a=b=c=d,∴四边形为菱形.
12.(1)平行四边形 (2)AB=AC≠BC (3)AB=AC=BC 【解析】(1)四边形ADEF
∴DE=AC=AF,FE=AB=AD,∴四边形ADEF是个平行四边形;(2)当△ABC为等腰三角形并且不是等边三角形时,即AB=AC时,由第(1)题中可知四边形ADEF的四边都相等,此时四边形ADEF是菱形;(3)当△ABC为等边三角形时,即AB=AC=BC时,四边形ADEF中的A点与E点重合,此时以A、D、E、F为顶点的四边形不存在.
13.45° 【解析】过点D作DE⊥BC于E,过点B作BF⊥CD于F,∴∠DEC=∠BFC=90°,∵两张宽度均为3cm的纸条交错叠放在一起,∴AD∥BC,AB∥CD,BF=DE=3,∴四边形ABCD是平行四边形,∵∠DCE=∠BCF,∴△DEC≌△BFC(AAS),∴BC=DC,∴四边形ABCD是菱形,∵两张纸片中重叠部分的面积为9cm2,∴BC?DE=9,∴BC=CD=3(cm),
∵∠DCE=∠α,由勾股定理得CE=DE=3,∴∠α=45°.
14.①②④ 【解析】①∵在平行四边形ABCD中,E、F分别为边AB、CD的中点
∴四边形DEBF为平行四边形,∴DE∥BF故①正确.②由①知四边形DEBF为平行四边形,
∵AD⊥BD,E为边AB的中点,∴DE=BE=AE,∴四边形BEDF是菱形故②正确.
③∵AG∥DB AD∥BG AD⊥BD∴AGBD为矩形,∴AD=BG=BC,要使FG⊥AB,则BF=BC=BG,不能证明BF=BC,即FG⊥AB不恒成立,故③不正确.
④由③知BC=BG,∴S△BFG=S△FCG,∵F为CD中点∴S△FCG=S平行四边形ABCD,∴S△BFG=故④正确.
15.证明:∵DE∥AC,DF∥AB,∴四边形AEDF为平行四边形.又∵∠1=∠2,而∠2=∠3,
∴∠1=∠3,∴AE=DE.∴=□AEDF为菱形.∴AD⊥EF.
17.证明:(1)在平行四边形ABCD中,AD∥BC,∴∠AEB=∠EAD,∵AE=AB,∴∠ABE=∠AEB,∴∠ABE=∠EAD;
(2)∵AD∥BC,∴∠ADB=∠DBE,∵∠ABE=∠AEB,∠AEB=2∠ADB,
∴∠ABE=2∠ADB,∴∠ABD=∠ABE﹣∠DBE=2∠ADB﹣∠ADB=∠ADB,
∴AB=AD,又∵四边形ABCD是平行四边形,∴四边形ABCD是菱形
18.证明:∵点E,F分别为AB,AD的中点∴AE=AB,AF=AD,又∵四边形ABCD是菱形,∴AB=AD,∴AE=AF,又∵菱形ABCD的对角线AC与BD相交于点O∴O为BD的中点,∴OE,OF是△ABD的中位线. ∴OE∥AD,OF∥AB,∴四边形AEOF是平行四边形,∵AE=AF,∴四边形AEOF是菱形.
19.(1)证明:∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC,又∵BE=2DE,EF=BE,∴EF=BC,EF∥BC,∴四边形BCFE是平行四边形,又∵BE=FE,∴四边形BCFE是菱形;(2)解:∵∠BCF=120°,∴∠EBC=60°,∴△EBC是等边三角形,∴菱形的边长为4,高为2,∴菱形的面积为4×2=8.
20.证明:(1)∵AE∥BC,DE∥AB,∴四边形ABDE是平行四边形,∴AE=BD,∵D是BC中点,∴DC=DB,∴AE=DC,AE∥DC,∴四边形ADCE是平行四边形,∴AD=EC;
(2)∵当∠BAC=90°时,AD是Rt△ABC斜边上的中线,∴AD=BC=CD,
∴四边形ADCE是菱形;(3)∵四边形ADCE是菱形,∴对角线AC⊥DE且O是DE中点,∵ABDE是平行四边形,∴AB=DE,又已知AB=AO∴AO=DE=2DO=2a,
在Rt△AOD中,可求出AD=,∴菱形ADCE的周长为4.
18.2.2 菱形的判定
1.回顾:
菱形的定义:
菱形的性质:
菱形的面积公式:
2.判定菱形的两个定理:
3.请写出判定菱形的两种思路:
4.(1)请判断下列哪些条件能判定四边形ABCD是菱形的有 .
①AC⊥BD,AC与BD互相平分
②AB=BC=CD=DA
③AB=BC,AD=CD,AC⊥BD
④AB=CD,AD=BC,AC⊥BD
(2)请判断下列哪些条件能判定□ABCD是菱形的有 .
①AC⊥BD
②∠BAD=90°
③AB=BC
④AC=BD
用菱形的定义判定
学会运用菱形的定义判定菱形.
【例1】如图,四边形ABCD为平行四边形,BD为对角线,点E在AB边的延长线上,作EF∥BD,交BC边于点F,BE=BF.求证:四边形ABCD是菱形.
分析:根据平行线性质和等腰三角形性质推出∠DBC=∠DBA,推出DC=BC,根据菱形的判定推出即可.
证明:∵EF∥BD,
∴∠E=∠ABD,∠EFB=∠DBC,
∵BE=BF,
∴∠E=∠EFB,
∴∠DBC=∠DBA,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CDB=∠DBA,
∴∠CDB=∠CBD,
∴DC=BC,
∴平行四边形ABCD是菱形.
练习1
如图,在□ABCD中,EF∥BD,分别交BC,CD于点P,Q,交AB,AD的延长线于点E,F.已知BE=BP.
求证:(1)∠E=∠F;
(2)□ABCD是菱形.
菱形的判定定理
学会用定理来判定菱形.
【例2】如图,过平行四边形ABCD对角线的交点O作两条互相垂直的直线EF、GH分别交平行四边形ABCD四边于E、G、F、H,求证:四边形EGFH是菱形.
分析:根据对角线互相垂直的平行四边形是菱形.由已知条件证明OH=OG,同理OE=OF,所以四边形EFGH是平行四边形,又因为EF⊥GH,所以四边形EGFH是菱形.
证明:如图,顺次连接点E、G、F、H.
在平行四边形ABCD中,OD=OB,OA=OC,AD∥CB,
∴∠OBG=∠HDO.
∴在△OBG与△ODE中, ∠OBG=∠ODH OB=OD ∠BOG=∠DOH ,
∴△OBG≌△ODE(ASA),
∴OH=OG.
同理OE=OF,
∴四边形EFH是平行四边形,
又∵EF⊥HG,
∴平行四边形EGFH是菱形.
练习2
如图,在△ABC中,AB=AC,AD是角平分线,E为AD延长线上一点,CF∥BE交AD于点F,连接BF、CE.四边形BECF是菱形吗?请说明理由.
【例3】如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
(1)请你判断所画四边形的形状,并说明理由;
(2)连接EF,若AE=8厘米,∠A=60°,求线段EF的长.
分析:(1)由AE=AF=ED=DF,根据四条边都相等的四边形是菱形,即可证得:四边形AEDF是菱形;
(2)首先连接EF,由AE=AF,∠A=60°,可证得△EAF是等边三角形,则可求得线段EF的长.
解:(1)菱形.
理由:∵根据题意得:AE=AF=ED=DF,
∴四边形AEDF是菱形;
(2)连接EF,
∵AE=AF,∠A=60°,
∴△EAF是等边三角形,
∴EF=AE=8厘米.
练习3
已知:如图所示,在△ABC中,AB=AC,D、E、F分别是AB、BC、AC边上的中点.
求证:四边形ADEF是菱形.
菱形的判定与性质
通过判定得到菱形,既而能用菱形的性质来求解问题.
【例4】如图,在□ABCD中,∠ABC=5∠A,过点B作BE⊥DC交AD的延长线于点E,O是垂足,且DE=DA=4cm,
求:四边形BDEC的周长和面积(结果可保留根号)
分析:根据题意可判定四边形BDEC是菱形,则可得其周长,求出AB和BE,即可求得面积.
解:∵四边形ABCD是平行四边形,
∴AB//CD,AD//BC,AD=BC,
又BE⊥CD,
∴AB⊥BE,
又AD=DE,
∴BD=DE=4cm.
∵DE=BC,DE//BC,
∴四边形BCDE是平行四边形,
∵BD=DE,
∴□BCDE是菱形.
其周长为16cm.
∵5∠A=∠ABC,∠A+∠ABC=180°,
∴∠A=30°.∴在Rt△ABE中,
BE=AE=4cm,
由勾股定理得AB=4cm,
则菱形BDEC的面积为:
CD·BE=cm2.
练习4
如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处.
(1)求证:△ABE≌△AGF;
(2)连接AC,若平行四边形ABCD的面积为8,,求AC?EF的值.
菱形的判定方法总结:
若已知某四边形,求证其为菱形:
首先看是否能用“四条边相等的四边形是菱形”来判定,如果不行,那么采用如下思路:根据已知条件先证明该四边形是平行四边形,然后再根据“一组邻边相等的平行四边形是菱形”或“对角线互相垂直的平行四边形是菱形”求证“有一组邻边相等”或“对角线互相垂直”即可请得.
1.(2013?海南)如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )
A.AB=BC
B.AC=BC
C.∠B=60°
D.∠ACB=60°
2.(2012?威海)如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AECF为菱形的是( )
A.AE=AF
B.EF⊥AC
C.∠B=60°
D.AC是∠EAF的平分线
3.(2011?甘孜州)如图,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A. AC、BD互相平分
B. BA=BC
C. AC=BD
D. AB∥CD
4.(2013?潍坊)如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 _________,使ABCD成为菱形(只需添加一个即可)
5..(2011?内江)如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足 _________ 条件时,四边形EFGH是菱形.
6.(2013?临沂)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
用时 分数
一、填空题(每题4分,共32分)
1.(2010?雅安)如图,要使□ABCD成为菱形,下列添加条件正确的是( )
A.AB⊥BC B.AC⊥BD
C.AC=BD D.∠ABC=∠CDA
2.能判定一个四边形是菱形的条件是( )
A. 对角线互相平分且相等
B. 对角线互相垂直且相等
C. 对角线互相垂直且对角相等
D. 对角线互相垂直,且一条对角线平分一组对角
3.如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论:①△BDF是等腰三角形;②DE=BC;③四边形ADFE是菱形;④∠BDF+∠FEC=2∠A,其中一定正确的是( )
A.①③④ B.②③④
C.①②④ D.①②③
4.已知□ABCD,添加下列一个条件:①AC⊥BD ②∠BAD=90° ③AB=BC ④AC=BD,其中能使□ABCD是菱形的为( )
A.①③ B.②③
C.③④ D.①②③
5.(2013?滨州)如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:
①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.
其中正确的个数是( )
A. 0 B. 1 C. 2 D. 3
6.如图,O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③四边形ABCD的面积为EF×BD;④∠ADE=∠EDO;⑤△DEF是轴对称图形.其中正确的结论有( )
A. 5个 B. 4个 C. 3个 D. 2个
7.如图,已知四边形ABCD的四边都相等,等边△AEF的顶点E、F分别在BC、CD上,且AE=AB,则∠C=( )
A.100° B.105°
C.110° D.120°
8.(2013?曲靖)如图,在?ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF.则四边形AECF是( )
A.梯形 B.矩形
C.菱形 D.正方形
二、填空题(每题3分,共18分)
9.(2008?南充)如图,四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点.请你添加一个条件,使四边形EFGH为菱形,应添加的条件是 .
10.在□ABCD中,若一条对角线平分
一个内角,则四边形ABCD为 形.
11.四边形的四条边长分别为a,b,c,d,满足条件a2+b2+c2=ab+bc+cd+da,则此四边形一定是 ______ .
12.如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF.
(1)四边形ADEF是 _________ ;
(2)当△ABC满足条件 _________ 时,四边形ADEF为菱形;
(3)当△ABC满足条件 _________ 时,四边形ADEF不存在.
13.如图,两张宽度均为3cm的纸条交错叠放在一起,相交成锐角α,且两张纸片中重叠部分的面积为9cm2,则锐角α的度数 _________ .
14.已知如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB,交CB的延长线于G,连接GF,若AD⊥BD.下列结论:
①DE∥BF;②四边形BEDF是菱形;③FG⊥AB;④S△BFG=S四边形ABCD
其中正确的是 _________ .
三、解答题(共40分)
15.(6分)(2002?咸宁)如图所示,已
知AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,
求证:AD⊥EF.
16.(6分)(2013?遂宁)如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是E、F,并且DE=DF.求证:
(1)△ADE≌△CDF;
(2)四边形ABCD是菱形.
17.(6分)(2013?盐城)如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD且AE=AB.
(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.
21世纪教育网版权所有
18.(6分)(2010?沈阳)如图,菱形ABCD的对角线AC与BD相交于点O,点E,F分别为边AB,AD的中点,连接EF,OE,OF,求证:四边形AEOF是菱形.
21世纪教育网版权所有
19.(8分)(2013?安顺)如图,在△ABC中,
D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
20.(8分)(2012?建宁县质检)如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形;
(3)在(2)的条件下,若AB=AO,且OD=a,求菱形ADCE的周长.
21世纪教育网版权所有
21世纪教育网版权所有
参考答案
基础为本、掌握新知
1.有一组邻边相等的平行四边形是菱形.
(1)边:四条边相等;两组对边平行且相等;
(2)角:两组对角相等;邻角互补;
(3)对角线:对角线互相平分且垂直;每一条对角线平分一组对角.
两条对角线之积的一半
2.有四条边相等的四边形是菱形;对角线互相垂直的平行四边形是菱形
3.(1)由四边形,证四条边相等,得菱形;(2)由四边形,先请其为平行四边形,再证其为菱形.
4.(1)①②④ (2)①③
一例一练、活用数学
练习1 证明:(1)∵BE=BP,∴∠E=∠BPE,∵BC∥AF,∴∠BPE=∠F,∴∠E=∠F. (2)∵EF∥BD,∴∠E=∠ABD,∠F=∠ADB,∴∠ABD=∠ADB,
∴AB=AD,∵四边形ABCD是平行四边形,∴□ABCD是菱形.
练习2 证明:∵AB=AC,AD是角平分线,∴BD=CD,∵CF∥BE,∴∠DBE=∠FCD,在△CDF和△BDE中,∠DBE=∠FCD,DB=CD,∠BDE=∠CDF,
∴△BDE≌△CDF(ASA),∴CF=BE,又∵CF∥BE,∴四边形BFCE是平行四边形;
∵AB=AC,D是BC的中点,∴AD⊥BC,又∵四边形BFCE是平行四边形,
∴四边形BFCE是菱形.
(2)解:连接CF,∵△ABE≌△AGF,∴AE=AF,根据翻折的性质EC=AE,∴EC=AE=AF,又∵AF∥EC,∴四边形AECF是平行四边形,根据翻折后点A、C重合,∴AC⊥EF,
∴□AECF是菱形,∴AC?EF=2×菱形AECF的面积,
∵□ABCD的面积=8,,∴△AEC的面积=×8×=,
∴菱形AECF的面积等于,∴AC?EF=2×菱形AECF的面积=.
全真考题、能力拓展
1.B 【解析】∵将△ABC沿BC方向平移得到△DCE,∴ABCD,∴四边形ABCD为平行四边形,当AC=BC时,平行四边形ACED是菱形.
2.C
3.A 【解析】A、∵AC、BD互相平分,∴四边形ABCD是平行四边形,
∵AC⊥BD(已知),∴平行四边形ABCD是菱形,故本选项正确;B、根据已知AC⊥BD和BA=BC不能推出四边形ABCD是平行四边形,即更不是菱形,故本选项错误;
C、根据已知AC⊥BD和AC=BD不能推出四边形ABCD是平行四边形,即更不是菱形,故本选项错误;D、根据已知AC⊥BD和AB∥DC不能推出四边形ABCD是平行四边形,即更不是菱形,故本选项错误.
4.OA=OC(答案不唯一)
(2)四边形ADCF是菱形,证明:AF∥BC,AF=DC,∴四边形ADCF是平行四边形,
∵AC⊥AB,AD是斜边BC的中线,∴AD=DC,∴平行四边形ADCF是菱形.
课时自测、认清自我
1.B 【解析】A、添加AB⊥BC,可以证明?ABCD是矩形,故此选项错误;
B、添加AC⊥BD,可以证明?ABCD是菱形,故此选项正确;
C、添加AC=BD,可以证明?ABCD是矩形,故此选项错误;
D、添加∠ABC=∠CDA不能证明?ABCD是菱形形,故此选项错误;
故选:B.
2.C 【解析】∵对角线互相垂直平分的四边形是菱形.∴A、B、D都不正确.
∵对角相等的四边形是平行四边形,而对角线互相垂直的平行四边形是菱形.
3.C 【解析】分别过点D、E作BC的垂线DG、EH;连接AF,∵折叠是轴对称图形,∴AF⊥DE,∵DE∥BC,∴AF⊥BC,且AM=MF,∴D、E分别是AB、AC的中点,
即;②DE=BC,正确.∵AD=DF,AE=EF,∴DA=DB=DF,∴①△BDF是等腰三角形,正确.∵DG∥AF∥EH,∴∠BDG=∠DAM,又∵DG是等腰三角形BDF的高,
∴∠BDF=2∠DAM,同理∠CEF=2∠EAM,∴④∠BDF+∠FEC=2∠A;如图显然③四边形ADFE是菱形是错误的.故选C.
4.A 【解析】∵四边形ABCD是平行四边形,①若AC⊥BD,则可得其为菱形,故①选项正确,②中∠BAD=90°,得到一矩形,不是菱形,所以②错误,③中一组邻边相等,也可得到一菱形,所以③成立,④中并不能得到其为矩形,菱形或正方形等,所以④不成立,
故A选项中①③都正确,B中②不成立,C中④错误,而D中多一个选项②也不对,
则能使□ABCD是菱形的有①或③.
5.D 【解析】△ABC、△DCE是等边三角形,∴∠ACB=∠DCE=60°,AC=CD,
∴∠ACD=180°﹣∠ACB﹣∠DCE=60°,∴△ACD是等边三角形,∴AD=AC=BC,故①正确;由①可得AD=BC,∵AB=CD,∴四边形ABCD是平行四边形,∴BD、AC互相平分,故②正确;由①可得AD=AC=CE=DE,故四边形ACED是菱形,即③正确.
6.B 【解析】①正确:∵E、F分别是OA、OC的中点.∴AE=OE.∵S△ADE=×AE×OD=×OE×OD=S△EOD∴S△ADE=S△EOD.②正确:∵四边形ABCD是菱形,E,F分别是OA,OC的中点.∴EF⊥OD,OE=OF.∵OD=OD.∴DE=DF.同理:BE=BF∴四边形BFDE是菱形.③正确:∵菱形ABCD的面积=AC×BD.∵E、F分别是OA、OC的中点.∴EF=AC.∴菱形ABCD的面积=EF×BD.④不正确:由已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO.⑤正确:∵EF⊥OD,OE=OF,OD=OD.
∴△DEO≌△DFO.∴△DEF是轴对称图形.∴正确的结论有四个,分别是①②③⑤.
7.A 【解析】∵四边形ABCD的四边都相等,∴四边形ABCD是菱形,∴∠B=∠D,∠A=∠C,AD∥BC,∴∠DAB+∠B=180°,∵△AEF是等边三角形,AE=AB,∴∠AEF=∠AFE=60°,AF=AD,∴∠B=∠AEB,∠D=∠AFD,由三角形的内角和定理得:∠BAE=∠FAD,设∠BAE=∠FAD=x,则∠D=∠AFD=180°﹣60°﹣2x,∵∠FAD+∠D+∠AFD=180°,
∴x+2(180°﹣60°﹣2x)=180°,解得:x=20°,∴∠C=∠BAD=2×20°+60°=100°,故选A.
8.C 【解析】四边形AECF是菱形,理由:∵在□ABCD中,对角线AC与BD相交于点O,∴AO=CO,∠AFO=∠CEO,∴在△AFO和△CEO中
,∴△AFO≌△CEO(AAS),∴FO=EO,∴四边形AECF平行四边形,
∵EF⊥AC,∴平行四边形AECF是菱形.
9.AC=BD(答案不唯一)
10.菱形 【解析】一条对角线平分一个内角,根据两直线平行内错角相等,等角对等边可求得此对角线和一组邻边组成的是等腰三角形,有一组邻边相等的平行四边形是菱形.故四边形ABCD是菱形.
11.菱形 【解析】∵a2+b2+c2+d2=ab+bc+cd+da∴2(a2+b2+c2+d2)﹣2ab﹣2bc﹣2cd﹣2da=0
∴(a﹣b)2+(b﹣c)2+(c﹣d)2+(d﹣a)2=0由非负数的性质可知:(a﹣b)=0,(b﹣c)=0,(c﹣d)=0,(a﹣d)=0,∴a=b=c=d,∴四边形为菱形.
12.(1)平行四边形 (2)AB=AC≠BC (3)AB=AC=BC 【解析】(1)四边形ADEF
∴DE=AC=AF,FE=AB=AD,∴四边形ADEF是个平行四边形;(2)当△ABC为等腰三角形并且不是等边三角形时,即AB=AC时,由第(1)题中可知四边形ADEF的四边都相等,此时四边形ADEF是菱形;(3)当△ABC为等边三角形时,即AB=AC=BC时,四边形ADEF中的A点与E点重合,此时以A、D、E、F为顶点的四边形不存在.
13.45° 【解析】过点D作DE⊥BC于E,过点B作BF⊥CD于F,∴∠DEC=∠BFC=90°,∵两张宽度均为3cm的纸条交错叠放在一起,∴AD∥BC,AB∥CD,BF=DE=3,∴四边形ABCD是平行四边形,∵∠DCE=∠BCF,∴△DEC≌△BFC(AAS),∴BC=DC,∴四边形ABCD是菱形,∵两张纸片中重叠部分的面积为9cm2,∴BC?DE=9,∴BC=CD=3(cm),
∵∠DCE=∠α,由勾股定理得CE=DE=3,∴∠α=45°.
14.①②④ 【解析】①∵在平行四边形ABCD中,E、F分别为边AB、CD的中点
∴四边形DEBF为平行四边形,∴DE∥BF故①正确.②由①知四边形DEBF为平行四边形,
∵AD⊥BD,E为边AB的中点,∴DE=BE=AE,∴四边形BEDF是菱形故②正确.
③∵AG∥DB AD∥BG AD⊥BD∴AGBD为矩形,∴AD=BG=BC,要使FG⊥AB,则BF=BC=BG,不能证明BF=BC,即FG⊥AB不恒成立,故③不正确.
④由③知BC=BG,∴S△BFG=S△FCG,∵F为CD中点∴S△FCG=S平行四边形ABCD,∴S△BFG=故④正确.
15.证明:∵DE∥AC,DF∥AB,∴四边形AEDF为平行四边形.又∵∠1=∠2,而∠2=∠3,
∴∠1=∠3,∴AE=DE.∴=□AEDF为菱形.∴AD⊥EF.
17.证明:(1)在平行四边形ABCD中,AD∥BC,∴∠AEB=∠EAD,∵AE=AB,∴∠ABE=∠AEB,∴∠ABE=∠EAD;
(2)∵AD∥BC,∴∠ADB=∠DBE,∵∠ABE=∠AEB,∠AEB=2∠ADB,
∴∠ABE=2∠ADB,∴∠ABD=∠ABE﹣∠DBE=2∠ADB﹣∠ADB=∠ADB,
∴AB=AD,又∵四边形ABCD是平行四边形,∴四边形ABCD是菱形
18.证明:∵点E,F分别为AB,AD的中点∴AE=AB,AF=AD,又∵四边形ABCD是菱形,∴AB=AD,∴AE=AF,又∵菱形ABCD的对角线AC与BD相交于点O∴O为BD的中点,∴OE,OF是△ABD的中位线. ∴OE∥AD,OF∥AB,∴四边形AEOF是平行四边形,∵AE=AF,∴四边形AEOF是菱形.
19.(1)证明:∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC,又∵BE=2DE,EF=BE,∴EF=BC,EF∥BC,∴四边形BCFE是平行四边形,又∵BE=FE,∴四边形BCFE是菱形;(2)解:∵∠BCF=120°,∴∠EBC=60°,∴△EBC是等边三角形,∴菱形的边长为4,高为2,∴菱形的面积为4×2=8.
20.证明:(1)∵AE∥BC,DE∥AB,∴四边形ABDE是平行四边形,∴AE=BD,∵D是BC中点,∴DC=DB,∴AE=DC,AE∥DC,∴四边形ADCE是平行四边形,∴AD=EC;
(2)∵当∠BAC=90°时,AD是Rt△ABC斜边上的中线,∴AD=BC=CD,
∴四边形ADCE是菱形;(3)∵四边形ADCE是菱形,∴对角线AC⊥DE且O是DE中点,∵ABDE是平行四边形,∴AB=DE,又已知AB=AO∴AO=DE=2DO=2a,
在Rt△AOD中,可求出AD=,∴菱形ADCE的周长为4.
