平面向量数量积的坐标表示[下学期]

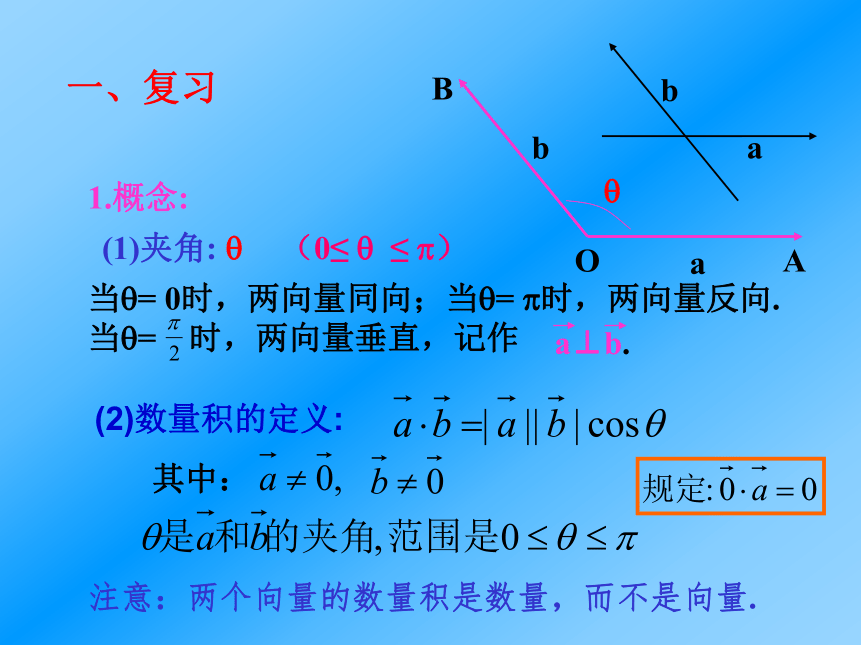
课件18张PPT。§5.7 平面向量的数量积的坐标表示一、复习1.概念:(1)夹角: ?(2)数量积的定义:注意：两个向量的数量积是数量，而不是向量.（0≤ ? ≤ ?）2.几何意义:3.性质: 设 ， 都是非零向量， 是与 方向相同的单位向量，?是 与 的夹角,则 用于计算向量的夹角4、数量积的运算律：⑴交换律：⑵对数乘的结合律：⑶分配律：注意：数量积不满足结合律从力的做功来看若力增大n倍则功增大n倍引例： 已知：A(2，1)，B(3，2)，C(–1，4)，
求证：?ABC是直角三角形.分析：先画图，问题：已知两个非零向量
怎样用和的坐标表示呢？OA
(x1，y1) B
(x2，y2)yx如图，我们先看x轴上的单位向量 和轴y上的单位向量 容易知道，
二、新课问题：已知两个非零向量怎样用 和 的坐标表示 呢？解：这就是说，两个向量的数量积等于它们对应坐标的乘积的和。即已知：A(2，1)，B(3，2)，C(–1，4)，
求证：?ABC是直角三角形.∴ AB⊥AC.证明：∴ ?ABC是直角三角形.数量积的主要性质的坐标表示：内积为零是判定两向量垂直的充要条件用于计算向量的模用于计算向量的夹角这就是平面内两点间的距离公式（1）求 ；（2）求 与 的夹角θ.解：（1）（2）例 2：已知 ＝(5, 0)， ＝(–3.2, 2.4), 求证：( ＋ )⊥ .证明：例3 已知 ，当k为何值时，
（1） 与 垂直？（2） 与 平行？ =k(1,2)+(－3,2)=(k－ 3,2k+2)
=(1,2) － 3(－ 3,2)=(10, －4)（1）若 与 垂直，则有
(k － 3) ×10+(2k+2) ×(－ 4)=0所以k=19（2）若 与 平行，则有(k － 3) × (－ 4) － (2k+2) × 10=0所以k= － .解：例 4：已知：A、B、C三点坐标分别为(2，0)、(4，2)、(0，4)，直线 l 过A、B两点，求点C到 l 的距离.分析一：如图， 为定H点坐标(两个未知数)， 可利用H点在 l 上，及CH⊥AB这两个条件.三、小结：（1）掌握平面向量数量积的坐标表示，即两个向量的数量积等于它们对应坐标的乘积之和；（2）要学会运用平面向量数量积的坐标表示解决有关长度、角度及垂直问题.今日作业（1）P123 练习;
（2）P123 习题5.7
第1、2、3、4、5题.