第二章 相交线与平行线 专项训练题(含解析)
文档属性
| 名称 | 第二章 相交线与平行线 专项训练题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 714.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-03 06:09:13 | ||
图片预览


文档简介
七年级下册第二章 相交线与平行线
一、单选题
1.下列说法正确的是( )
A.同位角相等
B.在同一平面内,如果a⊥b,b⊥c,则a⊥c
C.相等的角是对顶角
D.在同一平面内,如果a∥b,b∥c,则a∥c
2.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
3.如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的,第二次拐的,第三次拐的,这时的道路恰好和第一次拐弯之前的道路平行,则是( )
A. B. C. D.
4.一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A.10° B.15° C.18° D.30°
5.如果一个角的度数比它的补角的度数2倍多30°,那么这个角的度数是( )
A.50° B.70° C.130° D.160°
6.如图,直线,将一个直角三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为( )
A.30° B.32° C.42° D.58°
7.两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”,为了便于记忆,同学们可仿照图用双手表示“三线八角”(两大拇指代表被截直线,食指代表截线),下列三幅图依次表示( )
A.同位角、同旁内角、内错角 B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角 D.同位角、内错角、对顶角
8.如图所示,是平角,是射线,、分别是、的角平分线,若,则的度数为( )
A.56° B.62° C.72° D.124°
9.如图,已知直线,则∠α、∠β、∠γ之间的关系是( )
A. B.
C. D.
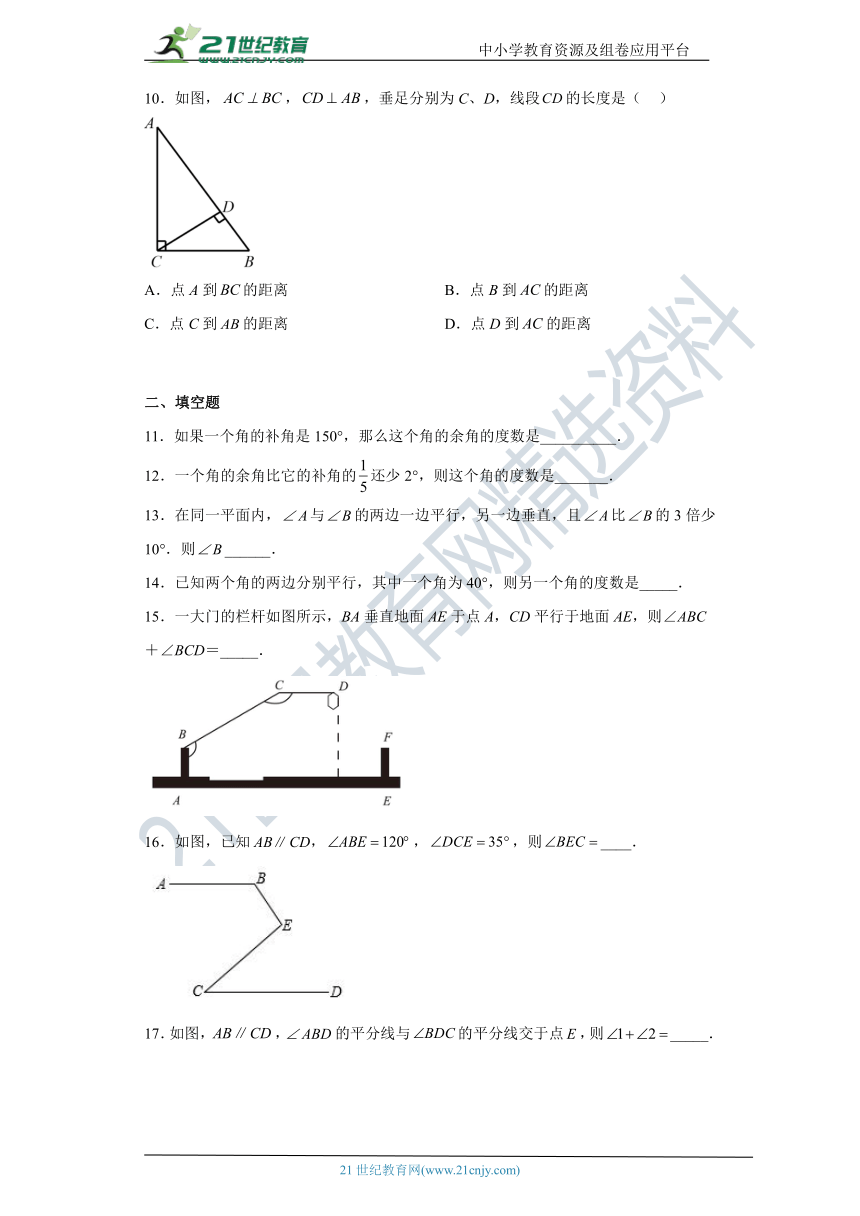
10.如图,,,垂足分别为C、D,线段的长度是( )
A.点A到的距离 B.点B到的距离
C.点C到的距离 D.点D到的距离
二、填空题
11.如果一个角的补角是150°,那么这个角的余角的度数是__________.
12.一个角的余角比它的补角的还少2°,则这个角的度数是_______.
13.在同一平面内,与的两边一边平行,另一边垂直,且比的3倍少10°.则______.
14.已知两个角的两边分别平行,其中一个角为40°,则另一个角的度数是_____.
15.一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=_____.
16.如图,已知ABCD,,,则____.
17.如图,,的平分线与的平分线交于点,则_____.
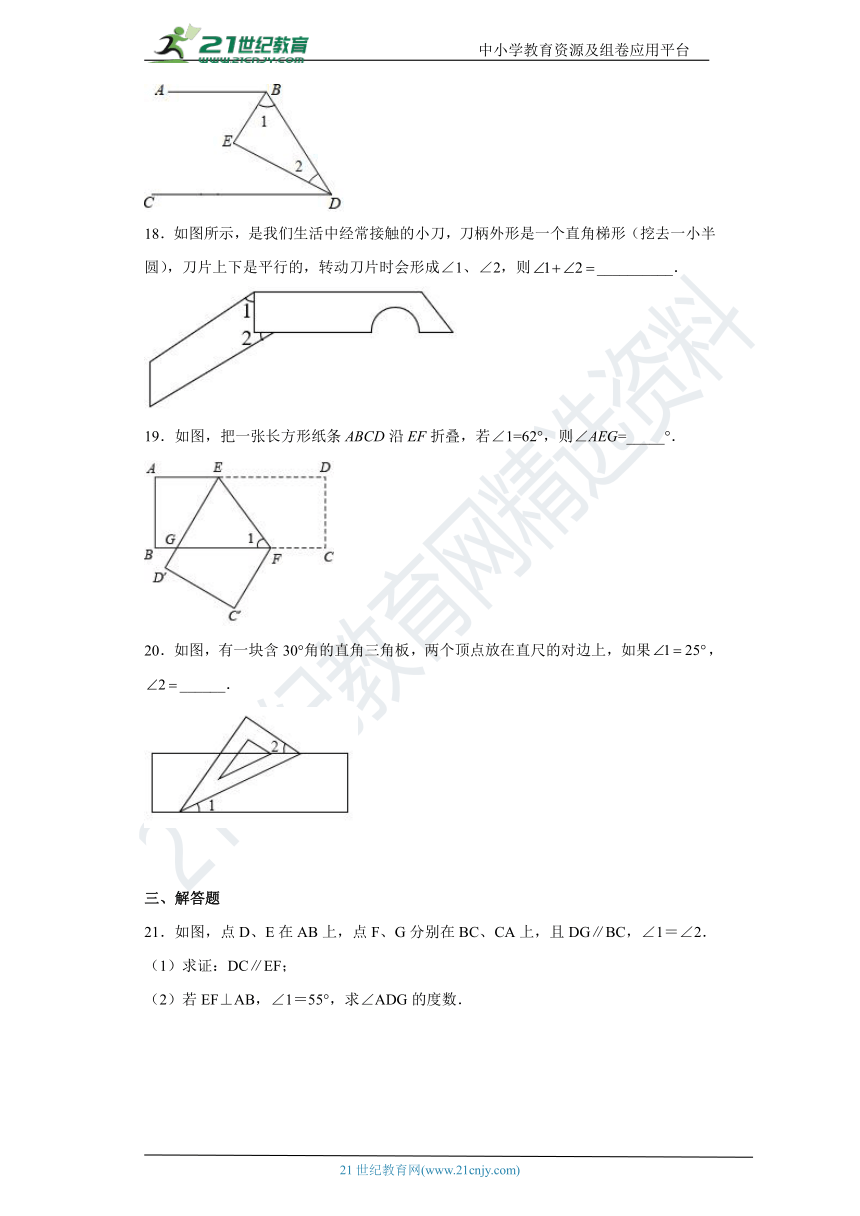
18.如图所示,是我们生活中经常接触的小刀,刀柄外形是一个直角梯形(挖去一小半圆),刀片上下是平行的,转动刀片时会形成∠1、∠2,则__________.
19.如图,把一张长方形纸条ABCD沿EF折叠,若∠1=62°,则∠AEG=_____°.
20.如图,有一块含30°角的直角三角板,两个顶点放在直尺的对边上,如果,______.
三、解答题
21.如图,点D、E在AB上,点F、G分别在BC、CA上,且DG∥BC,∠1=∠2.
(1)求证:DC∥EF;
(2)若EF⊥AB,∠1=55°,求∠ADG的度数.
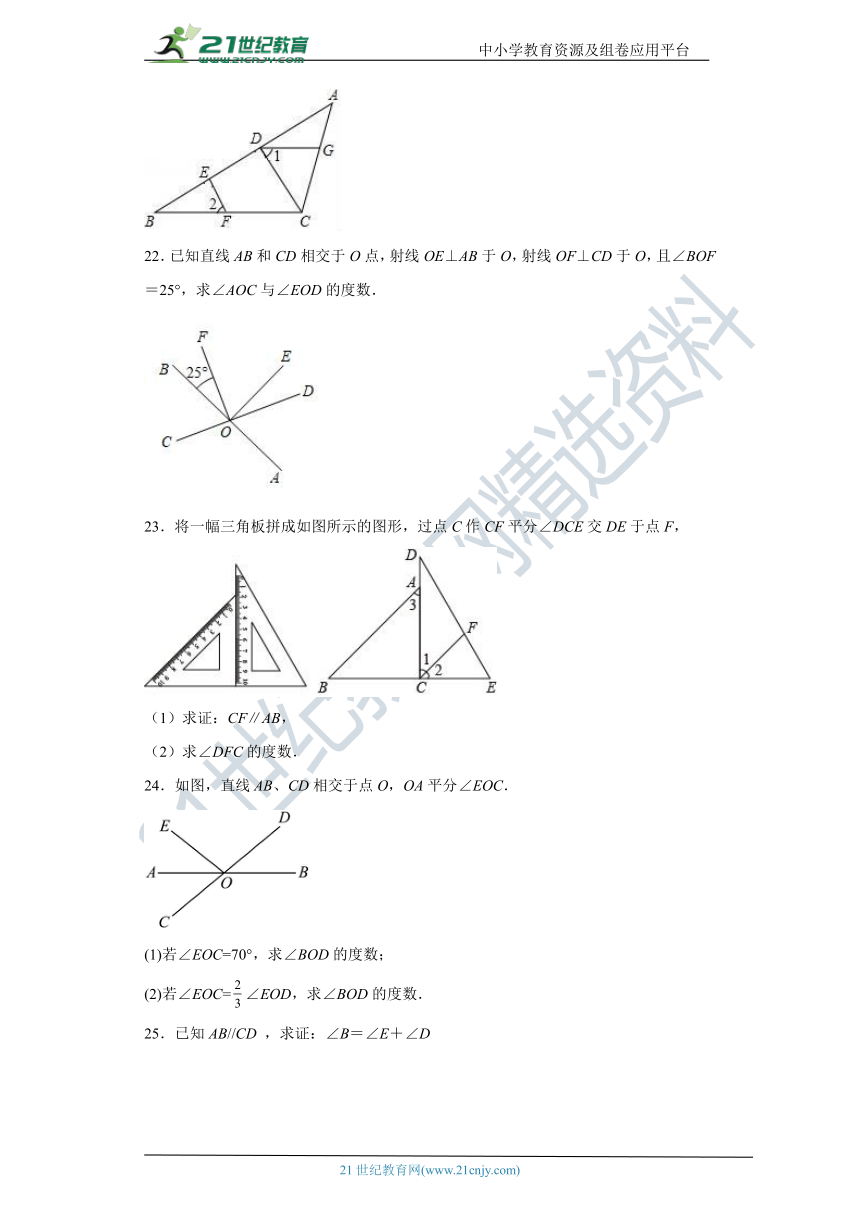
22.已知直线AB和CD相交于O点,射线OE⊥AB于O,射线OF⊥CD于O,且∠BOF=25°,求∠AOC与∠EOD的度数.
23.将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,
(1)求证:CF∥AB,
(2)求∠DFC的度数.
24.如图,直线AB、CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC=∠EOD,求∠BOD的度数.
25.已知AB//CD ,求证:∠B=∠E+∠D
26.如图,已知直线AB,CD相交于点O,射线OE把∠AOC分成两部分.
(1)写出图中∠AOC的对顶角 ,∠COE的补角是 ;
(2)已知∠AOC=60°,且∠COE:∠AOE=1:2,求∠DOE的度数.
27.已知:如图,D,E,F分别是AB,AC,BC上的点,DE∥BC,∠ADE=∠EFC,求证:∠1=∠2.
28.如图,直线AB、CD、MN相交于点O,FO⊥BO,OM平分∠DOF
(1)请直接写出图中所有与∠AON互余的角:.
(2)若∠AOC=∠FOM,求∠MOD与∠AON的度数.
29.如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠B=60°.试求∠ADG的度数.
30.如图,纸片三角形中,,,,将纸片的一角沿折叠,使点落在内的点上,求和的度数.
31.如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)若∠BOE=65°,求∠DOE的度数;
(2)若∠BOD:∠BOE=2:3,求∠AOF的度数.
32.如图,已知A、O、B三点共线,∠AOD=42°,∠COB=90°.
(1)求∠BOD的度数;
(2)若OE平分∠BOD,求∠COE的度数.
33.已知:如图,AB∥CD,∠1=∠2,∠3=∠4.
(1)求证:AD∥BE;
(2)若∠B=∠3=2∠2,求∠D的度数.
34.如图,已知点A、O、B在一条直线上,∠COD=90°,OE平分∠AOC,OF平分∠BOD,求∠EOF的度数.
35.已知点O为直线AB上一点,将直角三角板MON的直角顶点放在点O处,并在∠MON内部作射线OC.
(1)将三角板放置到如图所示位置,使OC恰好平分∠MOB,且∠BON=2∠NOC,求∠AOM的度数;
(2)若仍将三角板按照如图所示的方式放置,仅满足OC平分∠MOB,试猜想∠AOM与∠NOC之间的数量关系,并说明理由.
36.如图,直线、相交于点,为锐角,,平分
(1)图中与互余的角为__________;
(2)若,求的度数;
(3)图中与锐角互补角的个数随的度数变化而变化,直接写出与互补的角的个数及对应的的度数
37.已知如图,AB∥CD,试解决下列问题:
(1)∠1+∠2= ;
(2)∠1+∠2+∠3= ;
(3)∠1+∠2+∠3+∠4= ;
(4)试探究∠1+∠2+∠3+∠4+…+∠n= .
38.问题情境:如图1,,,.求 度数.
小明的思路是:如图2,过 作,通过平行线性质,可得 .
问题迁移:
(1)如图3,,点 在射线 上运动,当点 在 、 两点之间运动时,,. 、 、 之间有何数量关系 请说明理由;
(2)在(1)的条件下,如果点 在 、 两点外侧运动时(点 与点 、 、 三点不重合),请你直接写出 、 、 间的数量关系.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.D
【分析】根据同位角的定义、垂线的性质、对顶角的性质、平行公理依次判断.
【详解】解:A. 同位角不一定相等,故该项不符合题意;
B. 在同一平面内,如果a⊥b,b⊥c,则a//c,故该项不符合题意;
C. 相等的角不一定是对顶角,故该项不符合题意;
D. 在同一平面内,如果a//b,b//c,则a//c,故该项符合题意;
故选:D.
【点睛】此题考查了语句的判断,正确掌握同位角的定义、垂线的性质、对顶角的性质、平行公理是解题的关键.
2.B
【分析】根据所学的相关知识,逐一判断即可.
【详解】解:①两点之间的所有连线中,线段最短,故①说法正确.
②相等的角不一定是对顶角,故②说法错误.
③经过直线外一点有且只有一条直线与已知直线平行,故③说法错误.
④同一平面内,过一点有且只有一条直线与已知直线垂直,故④说法错误.
⑤两点之间的距离是两点间的线段的长度,故⑤说法错误.
⑥在同一平面内,两不重合的直线的位置关系只有两种:相交和平行,故⑥说法正确.
综上所述,正确的结论有2个.
故选:.
【点睛】本题主要考查对平行线的定义,两点间的距离,相交线等知识点的理解和掌握,能熟练地运用性质进行说理是解此题的关键.
3.D
【分析】过点B作直线BD与第一次拐弯的道路平行,由题意可得,进而可得,然后问题可求解.
【详解】解:过点B作直线BD与第一次拐弯的道路平行,如图所示:
∵第三次拐的,这时的道路恰好和第一次拐弯之前的道路平行,
∴直线BD与第三次拐弯的道路也平行,
∵,
∴,,
∵,
∴,
∴;
故选D.
【点睛】本题主要考查平行线的性质,熟练掌握平行线的性质是解题的关键.
4.B
【分析】直接利用三角板的特点,结合平行线的性质得出∠ABD=45°,进而得出答案.
【详解】解:由题意可得:∠EDF=45°,∠ABC=30°,
∵AB∥CF,
∴∠ABD=∠EDF=45°,
∴∠DBC=45°﹣30°=15°.
故选:B.
【点睛】本题考查的是平行线的性质,解题的关键是熟练掌握平行线的性质.
5.C
【分析】根据互为补角的定义结合已知条件列方程求解即可.
【详解】解:设这个角是,则它的补角是:,
根据题意,得:
,
解得:,
即这个角的度数为.
故选:C.
【点睛】此题考查了补角的知识,熟悉相关性质定义是解题的关键.
6.B
【详解】解:如图,过点A作,
∴∠3=∠1=58°,
∵∠3+∠4=90°,
∴∠4=90°﹣∠3=32°,
∵
∴,
∴∠2=∠4=32°,
故选B.
7.B
【分析】两条线a、b被第三条直线c所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角;两个角分别在截线的异侧,且夹在两条被截线之间,具有这样位置关系的一对角互为内错角;两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角,据此作答即可.
【详解】解:根据同位角、内错角、同旁内角的概念,可知
第一个图是同位角,第二个图是内错角,第三个图是同旁内角.
所以B选项是正确的,
故选B.
【点睛】本题考查了同位角、内错角、同旁内角的识别,属于简单题,解题的关键是掌握同位角、内错角、同旁内角,并能区别它们.
8.B
【分析】根据OE平分可求得∠BOC的度数,由∠AOC与∠BOC互补即可得到∠AOC的度数,由OD平分∠AOC, 即可求得∠AOD的度数.
【详解】∵平分
∴∠BOC=2∠COE=2×28°=56°
∵∠AOC+∠BOC=180°
∴∠AOC=180° ∠BOC=124°
∵平分
∴
故选:B
【点睛】本题考查了角平分线的性质、互补等知识,角平分线的性质熟练掌握相关知识点是关键.
9.D
【分析】过∠β顶点作AB的平行线,把∠β分成∠1和∠2,然后根据平行线的性质即可得到解答 .
【详解】解:如图,过∠β顶点作AB的平行线,把∠β分成∠1和∠2,
则∠1=∠α,∠2+∠γ=180°,∠1+∠2=∠β,
∴∠β+∠γ ∠α=180°,
故选D.
【点睛】本题考查平行线的应用,熟练掌握平行线的性质是解题关键 .
10.C
【分析】根据点到直线的距离等于垂线段的长度即可求解.
【详解】解:依题意,,,
点A到的距离是线段的长度,
点B到的距离是线段的长度,
点C到的距离是线段的长度
点D到的距离图中没有标出,
故选C
【点睛】本题考查了点到直线的距离的定义,数形结合以及理解定义是解题的关键.点到直线的距离的等于垂线段的长度.
11.60°##60度
【分析】首先根据补角的定义求得这个角的度数,然后根据余角的定义即可求出这个角的余角.
【详解】解:∵一个角的补角是150°,
∴这个角是180° 150°=30°,
∴这个角的余角是90° 30°=60°.
故答案是:60°.
【点睛】此题主要考查的是补角和余角的定义,属于基础题,较简单,主要记住互为余角的两个角的和为90°;互为补角的两个角的和为180°.
12.70°
【分析】设这个角的度数为x,由题意列出方程,解方程即可.
【详解】解:设这个角的度数为x,
根据题意得:90°-x=(180°-x)-2°,
解得:x=70°.
所以这个角的度数为70°.
故答案为:70°
【点睛】本题考查了余角和补角以及一元一次方程的应用;由题意列出方程是解题的关键.
13.25°或50°
【分析】根据平行线的性质以及垂直的定义即可求解.
【详解】解:∵与的两边一边平行,另一边垂直,
∴有两种情况,
如下图所示:
由题意得,AC∥BD,∠A=3∠B-10°,BC⊥AD
∵AC∥BD
∴∠C=∠B
∵BC⊥AD
∴∠A+∠C=90°
∴3∠B-10°+∠B=90°,
∴∠B=25°
如下图所示:
由题意得,AN∥BM,∠A=3∠B-10°,BH⊥AM
∵AN∥BM
∴∠A+∠M=180°,
∵BH⊥AM
∴∠B+∠M=90°
∴∠A-∠B=90°
∵∠A=3∠B-10°
3∠B﹣10°﹣∠B=90°,
∴∠B=50°,
综上所述,∠B的度数为25°或50°,
故答案:25°或50°.
【点睛】本题考查了平行线的性质,解题的关键是根据平行线的性质找出图中角度之间的关系.
14.40°或140°##140°或40°
【分析】由两角的两边互相平行可得这两个角相等或互补,再由其中一个角为 ,即可得出答案.
【详解】解:因为两个角的两边互相平行,
所以这两个角相等或互补,
若这两个角相等,因为其中一个角为,所以另一个角的度数为;
若这两个角互补,则另一个角的度数为 ;
故答案为或 .
【点睛】此题考查了平行线的性质和补角的定义,属于基本题型,正确分类,熟练掌握平行线的性质是关键.
15.270°
【分析】过B作BF∥AE,则CD∥BF∥AE.根据平行线的性质即可求解.
【详解】过B作BF∥AE,
∵CD∥ AE,
则CD∥BF∥AE,
∴∠BCD+∠1=180°,
又∵AB⊥AE,
∴AB⊥BF,
∴∠ABF=90°,
∴∠ABC+∠BCD=90°+180°=270°.
故答案为:270.
【点睛】本题主要考查了平行线的性质,两直线平行,同旁内角互补.正确作出辅助线是解题的关键.
16.95°
【分析】过点E作EF∥AB,可得∠BEF+∠ABE=180°,从而得到∠BEF=60°,再由AB//CD,可得∠FEC=∠DCE,从而得到∠FEC=35°,即可求解.
【详解】解:如图,过点E作EF∥AB,
∵EF//AB,
∴∠BEF+∠ABE=180°,
∵∠ABE=120°,
∴∠BEF=180°-∠ABE=180°-120°=60°,
∵EF//AB,AB//CD,
∴EF//CD,
∴∠FEC=∠DCE,
∵∠DCE=35°,
∴∠FEC=35°,
∴∠BEC=∠BEF+∠FEC=60°+35°=95°.
故答案为:95°
【点睛】本题主要考查了平行线的性质,熟练掌握两直线平行,同旁内角互补;两直线平行,内错角相等是解题的关键.
17.90°
【分析】根据平行线的性质可得,再根据角平分线的定义即可得出答案.
【详解】解:∵,∴,
∵是的平分线,∴,
∵是的平分线,∴,
∴,
故答案为.
【点睛】此题主要考查了平行线的性质,关键是掌握两直线平行,同旁内角互补.
18.
【分析】如图,过点O作OP∥AB,则AB∥OP∥CD.所以根据平行线的性质将(∠1+∠2)转化为(∠AOP+∠POC)来解答即可.
【详解】解:如图,过点O作OP∥AB,则∠1=∠AOP.
∵AB∥CD,
∴OP∥CD,
∴∠2=∠POC,
∵刀柄外形是一个直角梯形,
∴∠AOP+∠POC=90°,
∴∠1+∠2=90°.
【点睛】本题考查了平行线的性质和判定.平行线性质定理:两直线平行,同位角相等.两直线平行,同旁内角互补.两直线平行,内错角相等.
19.56
【分析】根据长方形的对边平行知AD∥BC,据此得∠DEF=∠EFB=62°,∠EGF=∠AEG再根据折叠变换的性质知∠GEF=∠DEF=62°,继而由∠AEG=180° ∠DEF ∠GEF可得答案.
【详解】解:由题意知AD∥BC,∠1=62°,
∴∠DEF=∠EFB=62°,∠EGF=∠AEG
根据折叠变换的性质知∠GEF=∠DEF=62°,
则∠AEG=180° ∠DEF ∠G′EF=56°,
∴∠EGF=56°
故答案为:56
【点睛】本题主要考查平行线的性质,解题的关键是掌握两直线平行内错角相等的性质、翻折变换的性质.
20.##35度
【分析】根据两直线平行内错角相等和含角的直角三角板的特点即可求解.
【详解】如图,根据题意可知,
∴,
∴.
故答案为:.
【点睛】本题主要考查平行线的性质.掌握两直线平行内错角相等是解题关键.
21.(1)见解析(2)35°
【分析】(1)由知∠1=∠DCF,则∠2=∠DCF,即可证明;
(2)由得∠B=90°-∠2=35°,再根据(1)可知的度数.
【详解】∵
∴∠1=∠DCF,
∵
∴∠2=∠DCF,
∴;
(2)∵,∴∠BEF=90°,
∴∠B=90°-∠2=35°,
又∵
∴=∠B=35°.
【点睛】此题主要考查平行线的性质与判定.
22.∠AOC=115°,∠EOD=25°
【分析】由OF⊥CD,得∠DOF =90°,根据条件可求出∠BOD的度数,即可得到∠AOC的度数;由OE⊥AB,得∠BOE =90°,可以推出∠EOF和∠EOD的度数.
【详解】解:∵OF⊥CD,
∴∠DOF=90°,
又∵∠BOF=25°,
∴∠BOD=∠DOF+∠BOF=90°+25°=115°,
∴∠AOC=∠BOD=115°,
又∵OE⊥AB,
∴∠BOE=90°,
∵∠BOF=25°,
∴∠EOF=∠BOE -∠BOF =65°,
∴∠EOD=∠DOF﹣∠EOF=90°-65°=25°.
【点睛】此题考查的知识点是垂线、角的计算及对顶角知识,关键是根据垂线的定义得出所求角与已知角的关系.
23.(1)证明见解析;(2)105°
【分析】(1)首先根据角平分线的性质可得∠1=45°,再有∠3=45°,再根据内错角相等两直线平行可判定出AB∥CF;
(2)利用三角形内角和定理进行计算即可.
【详解】解:(1)证明:∵CF平分∠DCE,
∴∠1=∠2=∠DCE.
∵∠DCE=90°,
∴∠1=45°.
∵∠3=45°,
∴∠1=∠3.
∴AB∥CF.
(2)∵∠D=30°,∠1=45°,
∴∠DFC=180°﹣30°﹣45°=105°.
【点睛】本题考查平行线的判定,角平分线的定义及三角形内角和定理,熟练掌握相关性质定理是本题的解题关键.
24.(1)35°;
(2)36°;
【分析】(1)根据角平分线的定义和对顶角相等计算求值即可;
(2)由∠EOC+∠EOD=180°和∠EOC=∠EOD求得∠EOC,再结合(1)解答计算求值即可;
【详解】(1)解: ∵OA平分∠EOC,
∴∠AOC=∠EOC,
∵∠EOC=70°,
∴∠AOC=×70°=35°,
∵直线AB、CD相交于点O,
∴∠BOD=∠AOC=35°;
(2)解:∵∠EOC=∠EOD,∠EOC+∠EOD=180°,
∴∠EOD +∠EOD=180°,
∴∠EOD =180°,
∴∠EOD =108°,
∴∠EOC=×108°=72°,
∵OA平分∠EOC,
∴∠AOC=∠EOC=×72°=36°,
∵直线AB、CD相交于点O,
∴∠BOD=∠AOC=36°;
【点睛】本题考查了相交线,与角平分线有关的角的计算,补角的定义;掌握对顶角的性质是解题关键.
25.见解析
【分析】过点E作EF∥CD,根据平行线的性质即可得出∠B=∠BOD,根据平行线的性质即可得出∠BOD=∠BEF、∠D=∠DEF,结合角之间的关系即可得出结论.
【详解】证明:过点E作EF∥CD,如图
∵AB∥CD,
∴∠B=∠BOD,
∵EF∥CD(辅助线),
∴∠BOD=∠BEF(两直线平行,同位角相等);∠D=∠DEF(两直线平行,内错角相等);
∴∠BEF=∠BED+∠DEF=∠BED+∠D(等量代换),
∴∠BOD=∠E+∠D(等量代换), 即∠B=∠E+∠D.
【点睛】本题考查了平行线的性质以及角的计算,解题的关键是根据平行线的性质找出相等或互补的角.
26.(1)∠BOD,∠DOE;(2)160°
【分析】(1)分析图形,根据对顶角和补角的定义可以求出答案;
(2)先设∠COE=x求得∠COE和∠AOE的度数,再根据邻补角的定义求得∠AOD的度数,然后将∠AOE与∠AOD的度数相加即可.
【详解】解:(1)由图形可知,∠AOC的对顶角是∠BOD,∠COE的补角是∠DOE;
(2)设∠COE=x,则∠AOE=2x,
∵∠AOC=60°,
∴x+2x=60,
解得x=20,
即∠COE=20°,∠AOE=40°,
∵∠AOC+∠AOD=180°,
∴∠AOD=120°,
∴∠DOE=∠AOE+∠AOD=40°+120°=160°.
【点睛】本题考查角的运算,解题的关键是正确找出图中的角的等量关系,本题属于基础题型.
27.见解析
【分析】先利用平行线的性质与已知,说明∠ABC与∠EFC的关系,再利用平行线的判定方法说明AB与EF的关系,最后利用平行线的性质得结论.
【详解】证明:∵DE∥BC,
∴∠ADE=∠ABC.
∵∠ADE=∠EFC,
∴∠ABC=∠EFC.
∴AB∥EF.
∴∠1=∠2.
【点睛】本题考查了平行线的性质和判定,掌握“两直线平行,同位(内错)角相等”“同位角相等,两直线平行”是解决本题的关键.
28.(1)∠FOM,∠MOD,∠CON;(2)20°,70°
【分析】(1)根据垂直的定义可得∠BOF=∠AOF=90°,由角平分线的定义和对顶角相等可得与∠AON互余的角有:∠FOM,∠MOD,∠CON;
(2)设∠MOD的度数为x°,用含x的式子表示出∠FOD和∠AOC的度数,然后由∠AOC=∠BOD,得出∠FOD+∠AOC=90°,据此列方程求解,再由(1)中∠MOD与∠AON互余可得出∠AON的度数.
【详解】解:(1)∵FO⊥BO,∴∠BOF=∠AOF=90°,
∴∠BOM+∠FOM=90°,
又∠BOM=∠AON,∴∠AON+∠FOM=90°.
∵OM平分∠DOF,∴∠DOM=∠FOM,
又∵∠DOM=∠CON,
∴与∠AON互余的角有:∠FOM,∠MOD,∠CON;
(2)设∠MOD的度数为x°,
∵OM平分∠FOD,
∴∠MOD=∠FOM=x°,
∴∠FOD=2x°,∠AOC=∠FOM=°,
又∵FO⊥BO,∠AOC=∠BOD,
∴∠FOD+∠AOC=90°,
即2x+=90,
解得:x=20.
即∠MOD=20°,
由(1)可知∠MOD与∠AON互余,
∴∠AON=90°-∠MOD=90°-20°=70°.
故∠MOD的度数为20°,∠AON的度数为70°.
【点睛】本题考查了垂直的定义,角的平分线的定义,余角的定义与性质以及对顶角相等,正确理解相关概念是关键.
29.60°
【分析】由CD⊥AB,FE⊥AB,则,则∠2=∠4,从而证得,得∠B=∠ADG,则答案可解.
【详解】解:CD⊥AB于D,FE⊥AB于E,
∴,
∴∠2=∠4,
又∵∠1=∠2,
∴∠1=∠4,
∴,
∴.
【点睛】本题考查了平行线的判定和性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.
30.
【分析】根据题意,已知,,可结合平行线性质以及平角的定义即可求解.
【详解】解: ∵,,,
∴,
由折叠可知:,
∴.
【点睛】本题主要是考查了折叠的性质、平角的定义、平行线的性质;掌握以上知识点是解题的关键.
31.(1)115°;(2)45°
【分析】(1)根据角平分线的定义,得出∠EOC=∠BOE=65°,利用邻补角定义求出∠DOE即可;
(2)根据角平分线的定义,∠BOD:∠BOE=2:3,求出∠BOD,再根据对顶角可求出∠AOC,利用垂直,求出∠AOF.
【详解】(1)∵OE平分∠BOC,∠BOE=65°,
∴∠EOC=∠BOE=65°,
∴∠DOE=180°-∠EOC=180°-65°=115°;
(2)∵OE平分∠BOC,
∴∠EOC=∠BOE,
∵∠BOD:∠BOE=2:3,
设∠BOD=x,则∠COE=∠BOE=,
∵∠COE+∠BOE+∠BOD=180°,
∴,
∴x=45°,
∵OF⊥CD,∠BOD=∠AOC,
∴∠BOD=∠AOC=45°,
∴∠COF=90°,
∴∠AOF=∠COF-∠AOC=90°-45°=45°.
【点睛】本题考查了角平分线定义,邻补角定义,对顶角性质,垂直定义,角的计算等;正确找出各个角之间的关系是正确计算的关键.
32.(1)∠BOD =138°;(2)∠COE=21°.
【分析】(1)根据平角的定义即可得到结论;
(2)根据余角的性质得到∠COD=48°,根据角平分线的定义即可得到结论.
【详解】(1)∵A、O、B三点共线,∠AOD=42°,
∴∠BOD=180°﹣∠AOD=138°;
(2)∵∠COB=90°,
∴∠AOC=90°,
∵∠AOD=42°,
∴∠COD=48°,
∵OE平分∠BOD,
∴∠DOE=∠BOD=69°,
∴∠COE=69°﹣48°=21°.
【点睛】本题考查了余角和补角的知识,属于基础题,互余的两角之和为90°,互补的两角之和为180°是需要同学们熟练掌握的内容.
33.(1)证明见解析;(2)72°.
【分析】根据平行线的性质推出∠1=∠ACD,求出∠2=∠ACD,根据∠2+∠CAF=∠ACD+∠CAF推出∠DAC=∠4,求出∠DAC=∠3,根据平行线的判定得出即可.根据平行线性质可求得∠D=∠DCE.
【详解】(1)证明:∵AB∥CD,
∴∠1=∠ACD,
∵∠BCD=∠4+∠E,
∵∠3=∠4,
∴∠1=∠E,
∵∠1=∠2,
∴∠2=∠E,
∴AD∥BE;
(2)解:∵∠B=∠3=2∠2,∠1=∠2,
∴∠B=∠3=2∠1,
∵∠B+∠3+∠1=180°,
即2∠1+2∠1+∠1=180°,解得∠1=36°,
∴∠B=2∠1=72°,
∵AB∥CD,
∴∠DCE=∠B=72°,
∵AD∥BE,
∴∠D=∠DCE=72°.
【点睛】本题考查了平行线的性质和判定,三角形的外角性质的应用,能推出∠4=∠DAC=∠3是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.
34.135°
【分析】直接利用角平分线的定义得出,进而得出答案.
【详解】解:∵点A、O、B在一条直线上,∠COD=90°,
∴∠AOC+∠BOD=90°,
∵OE平分∠AOC,OF平分∠BOD,
∴∠AOE=∠COE=∠AOC,
∠DOF=∠BOF=∠DOB,
∴∠COE+∠DOF=×90°=45°,
∴∠EOF的度数为:90°+45°=135°.
【点睛】此题主要考查了角的计算以及角平分线的定义,正确得出∠COE+∠DOF=45°是解题关键.
35.(1)∠AOM=45°;(2)∠AOM=2∠NOC.理由见解析.
【分析】(1)根据互余、互补、角平分线的意义,得出各个角之间的关系,从而求出答案;
(2)设未知数,表示图中的各个角,再利用互补得出结论.
【详解】解:(1),平分,
,
,
,
,
,
;
(2).
令为,为,,
,
,
,即,
.
【点睛】考查角平分线的意义、互补、互余的意义,正确表示各个角,理清各个角之间的关系是得出正确结论的关键.
36.(1)、;(2);(3)见解析.
【分析】(1)根据余角的定义可解答;
(2)根据补角的定义列方程可解答;
(3)设出∠AOE的度数,依次表达图中的补角,可解.
【详解】(1)由题意可得于∠AOE互余的角为:、
(2)设.
∵,
∴,
.
∵,
∴.
又∵,
∴,即.
∴.
(3)设∠AOE=α,且0°<α<90°由(1)可知,∠AOD=∠BOC=90°-α,∠BOE=180°-α,
∴∠BOD=180°-∠AOD=180°-(90°-α)=90°+α,
∵OF平分∠BOD,
∴∠BOF=∠DOF=45°+,
∴∠AOF=∠AOD+∠DOF=90°-α+45°+=135°-,
∠EOF=∠AOF+∠AOE=135°+,
∠COF=∠BOC+∠BOF=90°-α+45°+=135°-=∠AOF,
①当∠AOF+∠AOE=180°时,即135°-+α=180°,解得α=90°,不符合题意;
②当∠EOF+∠AOE=180°时,即135°++α=180°,解得α=30°,符合题意;
③当∠BOD+∠AOE=180°时,即90°+α+α=180°,解得α=45°,符合题意;
综上可知,
当锐角时,互补角有2个,为、.
当锐角时,互补角有3个,为、、.
当锐角不等于和时,互补角有1个,为.
【点睛】本题主要考查补角的定义,角平分线的定义,熟练掌握补角的定义是解题关键.
37.(1)180°;(2)360°;(3)540°;(4)(n﹣1)180°
【详解】(1)
故答案为:180°,
(2)作
故答案为:360°;
(3)过E作EM∥AB,过F作FN∥AB,
∵AB∥CD,
∴AB∥EM∥FN∥CD,
∴∠1+∠AEM=180°,∠MEF+∠EFN=180°,∠NFC+∠4=180°,
∴∠1+∠AEF+∠EFC+∠4=3×180°=540°,
故答案为:540°;
(4)根据(1)(2)(3)的结果可知:∠1+∠2+∠3+∠4+…+∠n=180(n-1)°,
故答案为:180(n-1)°.
38.(1)∠CPD=∠α+∠β,理由见解析;(2)①当点P在A、M两点之间时,∠CPD=∠β ∠α;②当点P在B、O两点之间时,∠CPD=∠α ∠β
【分析】(1)过点P作PE∥AD交CD于点E,根据题意得出AD∥PE∥BC,从而利用平行线性质可知=∠DPE,=∠CPE,据此进一步证明即可;
(2)根据题意分当点P在A、M两点之间时以及当点P在B、O两点之间时两种情况逐一分析讨论即可.
【详解】(1)∠CPD=,理由如下:
如图3,过点P作PEAD交CD于点E,
∵ADBC,PEAD
∴ADPEBC
∴=∠DPE,=∠CPE
∴∠CPD=∠DPE+∠CPE=;
(2)①当点P在A、M两点之间时,∠CPD=,理由如下:
如图4,过点P作PEAD交CD于点E
∵ADBC,PEAD
∴ADPEBC
∴=∠EPD,=∠CPE
∴∠CPD=∠CPE ∠EPD=;
②当点P在B、O两点之间时,∠CPD=,理由如下:
如图5,过点P作PEAD交CD于点E
∵ADBC,PEAD
∴ADPEBC
∴=∠DPE,=∠CPE
∴∠CPD=∠DPE ∠CPE=
综上所述,当点P在A、M两点之间时,∠CPD=∠β ∠α;当点P在B、O两点之间时,∠CPD=∠α ∠β.
【点睛】本题主要考查了在平行线性质及判定的综合运用,熟练掌握相关概念是解题关键.
一、单选题
1.下列说法正确的是( )
A.同位角相等
B.在同一平面内,如果a⊥b,b⊥c,则a⊥c
C.相等的角是对顶角
D.在同一平面内,如果a∥b,b∥c,则a∥c
2.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
3.如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的,第二次拐的,第三次拐的,这时的道路恰好和第一次拐弯之前的道路平行,则是( )
A. B. C. D.
4.一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A.10° B.15° C.18° D.30°
5.如果一个角的度数比它的补角的度数2倍多30°,那么这个角的度数是( )
A.50° B.70° C.130° D.160°
6.如图,直线,将一个直角三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为( )
A.30° B.32° C.42° D.58°
7.两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”,为了便于记忆,同学们可仿照图用双手表示“三线八角”(两大拇指代表被截直线,食指代表截线),下列三幅图依次表示( )
A.同位角、同旁内角、内错角 B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角 D.同位角、内错角、对顶角
8.如图所示,是平角,是射线,、分别是、的角平分线,若,则的度数为( )
A.56° B.62° C.72° D.124°
9.如图,已知直线,则∠α、∠β、∠γ之间的关系是( )
A. B.
C. D.
10.如图,,,垂足分别为C、D,线段的长度是( )
A.点A到的距离 B.点B到的距离
C.点C到的距离 D.点D到的距离
二、填空题
11.如果一个角的补角是150°,那么这个角的余角的度数是__________.
12.一个角的余角比它的补角的还少2°,则这个角的度数是_______.
13.在同一平面内,与的两边一边平行,另一边垂直,且比的3倍少10°.则______.
14.已知两个角的两边分别平行,其中一个角为40°,则另一个角的度数是_____.
15.一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=_____.
16.如图,已知ABCD,,,则____.
17.如图,,的平分线与的平分线交于点,则_____.
18.如图所示,是我们生活中经常接触的小刀,刀柄外形是一个直角梯形(挖去一小半圆),刀片上下是平行的,转动刀片时会形成∠1、∠2,则__________.
19.如图,把一张长方形纸条ABCD沿EF折叠,若∠1=62°,则∠AEG=_____°.
20.如图,有一块含30°角的直角三角板,两个顶点放在直尺的对边上,如果,______.
三、解答题
21.如图,点D、E在AB上,点F、G分别在BC、CA上,且DG∥BC,∠1=∠2.
(1)求证:DC∥EF;
(2)若EF⊥AB,∠1=55°,求∠ADG的度数.
22.已知直线AB和CD相交于O点,射线OE⊥AB于O,射线OF⊥CD于O,且∠BOF=25°,求∠AOC与∠EOD的度数.
23.将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,
(1)求证:CF∥AB,
(2)求∠DFC的度数.
24.如图,直线AB、CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC=∠EOD,求∠BOD的度数.
25.已知AB//CD ,求证:∠B=∠E+∠D
26.如图,已知直线AB,CD相交于点O,射线OE把∠AOC分成两部分.
(1)写出图中∠AOC的对顶角 ,∠COE的补角是 ;
(2)已知∠AOC=60°,且∠COE:∠AOE=1:2,求∠DOE的度数.
27.已知:如图,D,E,F分别是AB,AC,BC上的点,DE∥BC,∠ADE=∠EFC,求证:∠1=∠2.
28.如图,直线AB、CD、MN相交于点O,FO⊥BO,OM平分∠DOF
(1)请直接写出图中所有与∠AON互余的角:.
(2)若∠AOC=∠FOM,求∠MOD与∠AON的度数.
29.如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠B=60°.试求∠ADG的度数.
30.如图,纸片三角形中,,,,将纸片的一角沿折叠,使点落在内的点上,求和的度数.
31.如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)若∠BOE=65°,求∠DOE的度数;
(2)若∠BOD:∠BOE=2:3,求∠AOF的度数.
32.如图,已知A、O、B三点共线,∠AOD=42°,∠COB=90°.
(1)求∠BOD的度数;
(2)若OE平分∠BOD,求∠COE的度数.
33.已知:如图,AB∥CD,∠1=∠2,∠3=∠4.
(1)求证:AD∥BE;
(2)若∠B=∠3=2∠2,求∠D的度数.
34.如图,已知点A、O、B在一条直线上,∠COD=90°,OE平分∠AOC,OF平分∠BOD,求∠EOF的度数.
35.已知点O为直线AB上一点,将直角三角板MON的直角顶点放在点O处,并在∠MON内部作射线OC.
(1)将三角板放置到如图所示位置,使OC恰好平分∠MOB,且∠BON=2∠NOC,求∠AOM的度数;
(2)若仍将三角板按照如图所示的方式放置,仅满足OC平分∠MOB,试猜想∠AOM与∠NOC之间的数量关系,并说明理由.
36.如图,直线、相交于点,为锐角,,平分
(1)图中与互余的角为__________;
(2)若,求的度数;
(3)图中与锐角互补角的个数随的度数变化而变化,直接写出与互补的角的个数及对应的的度数
37.已知如图,AB∥CD,试解决下列问题:
(1)∠1+∠2= ;
(2)∠1+∠2+∠3= ;
(3)∠1+∠2+∠3+∠4= ;
(4)试探究∠1+∠2+∠3+∠4+…+∠n= .
38.问题情境:如图1,,,.求 度数.
小明的思路是:如图2,过 作,通过平行线性质,可得 .
问题迁移:
(1)如图3,,点 在射线 上运动,当点 在 、 两点之间运动时,,. 、 、 之间有何数量关系 请说明理由;
(2)在(1)的条件下,如果点 在 、 两点外侧运动时(点 与点 、 、 三点不重合),请你直接写出 、 、 间的数量关系.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.D
【分析】根据同位角的定义、垂线的性质、对顶角的性质、平行公理依次判断.
【详解】解:A. 同位角不一定相等,故该项不符合题意;
B. 在同一平面内,如果a⊥b,b⊥c,则a//c,故该项不符合题意;
C. 相等的角不一定是对顶角,故该项不符合题意;
D. 在同一平面内,如果a//b,b//c,则a//c,故该项符合题意;
故选:D.
【点睛】此题考查了语句的判断,正确掌握同位角的定义、垂线的性质、对顶角的性质、平行公理是解题的关键.
2.B
【分析】根据所学的相关知识,逐一判断即可.
【详解】解:①两点之间的所有连线中,线段最短,故①说法正确.
②相等的角不一定是对顶角,故②说法错误.
③经过直线外一点有且只有一条直线与已知直线平行,故③说法错误.
④同一平面内,过一点有且只有一条直线与已知直线垂直,故④说法错误.
⑤两点之间的距离是两点间的线段的长度,故⑤说法错误.
⑥在同一平面内,两不重合的直线的位置关系只有两种:相交和平行,故⑥说法正确.
综上所述,正确的结论有2个.
故选:.
【点睛】本题主要考查对平行线的定义,两点间的距离,相交线等知识点的理解和掌握,能熟练地运用性质进行说理是解此题的关键.
3.D
【分析】过点B作直线BD与第一次拐弯的道路平行,由题意可得,进而可得,然后问题可求解.
【详解】解:过点B作直线BD与第一次拐弯的道路平行,如图所示:
∵第三次拐的,这时的道路恰好和第一次拐弯之前的道路平行,
∴直线BD与第三次拐弯的道路也平行,
∵,
∴,,
∵,
∴,
∴;
故选D.
【点睛】本题主要考查平行线的性质,熟练掌握平行线的性质是解题的关键.
4.B
【分析】直接利用三角板的特点,结合平行线的性质得出∠ABD=45°,进而得出答案.
【详解】解:由题意可得:∠EDF=45°,∠ABC=30°,
∵AB∥CF,
∴∠ABD=∠EDF=45°,
∴∠DBC=45°﹣30°=15°.
故选:B.
【点睛】本题考查的是平行线的性质,解题的关键是熟练掌握平行线的性质.
5.C
【分析】根据互为补角的定义结合已知条件列方程求解即可.
【详解】解:设这个角是,则它的补角是:,
根据题意,得:
,
解得:,
即这个角的度数为.
故选:C.
【点睛】此题考查了补角的知识,熟悉相关性质定义是解题的关键.
6.B
【详解】解:如图,过点A作,
∴∠3=∠1=58°,
∵∠3+∠4=90°,
∴∠4=90°﹣∠3=32°,
∵
∴,
∴∠2=∠4=32°,
故选B.
7.B
【分析】两条线a、b被第三条直线c所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角;两个角分别在截线的异侧,且夹在两条被截线之间,具有这样位置关系的一对角互为内错角;两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角,据此作答即可.
【详解】解:根据同位角、内错角、同旁内角的概念,可知
第一个图是同位角,第二个图是内错角,第三个图是同旁内角.
所以B选项是正确的,
故选B.
【点睛】本题考查了同位角、内错角、同旁内角的识别,属于简单题,解题的关键是掌握同位角、内错角、同旁内角,并能区别它们.
8.B
【分析】根据OE平分可求得∠BOC的度数,由∠AOC与∠BOC互补即可得到∠AOC的度数,由OD平分∠AOC, 即可求得∠AOD的度数.
【详解】∵平分
∴∠BOC=2∠COE=2×28°=56°
∵∠AOC+∠BOC=180°
∴∠AOC=180° ∠BOC=124°
∵平分
∴
故选:B
【点睛】本题考查了角平分线的性质、互补等知识,角平分线的性质熟练掌握相关知识点是关键.
9.D
【分析】过∠β顶点作AB的平行线,把∠β分成∠1和∠2,然后根据平行线的性质即可得到解答 .
【详解】解:如图,过∠β顶点作AB的平行线,把∠β分成∠1和∠2,
则∠1=∠α,∠2+∠γ=180°,∠1+∠2=∠β,
∴∠β+∠γ ∠α=180°,
故选D.
【点睛】本题考查平行线的应用,熟练掌握平行线的性质是解题关键 .
10.C
【分析】根据点到直线的距离等于垂线段的长度即可求解.
【详解】解:依题意,,,
点A到的距离是线段的长度,
点B到的距离是线段的长度,
点C到的距离是线段的长度
点D到的距离图中没有标出,
故选C
【点睛】本题考查了点到直线的距离的定义,数形结合以及理解定义是解题的关键.点到直线的距离的等于垂线段的长度.
11.60°##60度
【分析】首先根据补角的定义求得这个角的度数,然后根据余角的定义即可求出这个角的余角.
【详解】解:∵一个角的补角是150°,
∴这个角是180° 150°=30°,
∴这个角的余角是90° 30°=60°.
故答案是:60°.
【点睛】此题主要考查的是补角和余角的定义,属于基础题,较简单,主要记住互为余角的两个角的和为90°;互为补角的两个角的和为180°.
12.70°
【分析】设这个角的度数为x,由题意列出方程,解方程即可.
【详解】解:设这个角的度数为x,
根据题意得:90°-x=(180°-x)-2°,
解得:x=70°.
所以这个角的度数为70°.
故答案为:70°
【点睛】本题考查了余角和补角以及一元一次方程的应用;由题意列出方程是解题的关键.
13.25°或50°
【分析】根据平行线的性质以及垂直的定义即可求解.
【详解】解:∵与的两边一边平行,另一边垂直,
∴有两种情况,
如下图所示:
由题意得,AC∥BD,∠A=3∠B-10°,BC⊥AD
∵AC∥BD
∴∠C=∠B
∵BC⊥AD
∴∠A+∠C=90°
∴3∠B-10°+∠B=90°,
∴∠B=25°
如下图所示:
由题意得,AN∥BM,∠A=3∠B-10°,BH⊥AM
∵AN∥BM
∴∠A+∠M=180°,
∵BH⊥AM
∴∠B+∠M=90°
∴∠A-∠B=90°
∵∠A=3∠B-10°
3∠B﹣10°﹣∠B=90°,
∴∠B=50°,
综上所述,∠B的度数为25°或50°,
故答案:25°或50°.
【点睛】本题考查了平行线的性质,解题的关键是根据平行线的性质找出图中角度之间的关系.
14.40°或140°##140°或40°
【分析】由两角的两边互相平行可得这两个角相等或互补,再由其中一个角为 ,即可得出答案.
【详解】解:因为两个角的两边互相平行,
所以这两个角相等或互补,
若这两个角相等,因为其中一个角为,所以另一个角的度数为;
若这两个角互补,则另一个角的度数为 ;
故答案为或 .
【点睛】此题考查了平行线的性质和补角的定义,属于基本题型,正确分类,熟练掌握平行线的性质是关键.
15.270°
【分析】过B作BF∥AE,则CD∥BF∥AE.根据平行线的性质即可求解.
【详解】过B作BF∥AE,
∵CD∥ AE,
则CD∥BF∥AE,
∴∠BCD+∠1=180°,
又∵AB⊥AE,
∴AB⊥BF,
∴∠ABF=90°,
∴∠ABC+∠BCD=90°+180°=270°.
故答案为:270.
【点睛】本题主要考查了平行线的性质,两直线平行,同旁内角互补.正确作出辅助线是解题的关键.
16.95°
【分析】过点E作EF∥AB,可得∠BEF+∠ABE=180°,从而得到∠BEF=60°,再由AB//CD,可得∠FEC=∠DCE,从而得到∠FEC=35°,即可求解.
【详解】解:如图,过点E作EF∥AB,
∵EF//AB,
∴∠BEF+∠ABE=180°,
∵∠ABE=120°,
∴∠BEF=180°-∠ABE=180°-120°=60°,
∵EF//AB,AB//CD,
∴EF//CD,
∴∠FEC=∠DCE,
∵∠DCE=35°,
∴∠FEC=35°,
∴∠BEC=∠BEF+∠FEC=60°+35°=95°.
故答案为:95°
【点睛】本题主要考查了平行线的性质,熟练掌握两直线平行,同旁内角互补;两直线平行,内错角相等是解题的关键.
17.90°
【分析】根据平行线的性质可得,再根据角平分线的定义即可得出答案.
【详解】解:∵,∴,
∵是的平分线,∴,
∵是的平分线,∴,
∴,
故答案为.
【点睛】此题主要考查了平行线的性质,关键是掌握两直线平行,同旁内角互补.
18.
【分析】如图,过点O作OP∥AB,则AB∥OP∥CD.所以根据平行线的性质将(∠1+∠2)转化为(∠AOP+∠POC)来解答即可.
【详解】解:如图,过点O作OP∥AB,则∠1=∠AOP.
∵AB∥CD,
∴OP∥CD,
∴∠2=∠POC,
∵刀柄外形是一个直角梯形,
∴∠AOP+∠POC=90°,
∴∠1+∠2=90°.
【点睛】本题考查了平行线的性质和判定.平行线性质定理:两直线平行,同位角相等.两直线平行,同旁内角互补.两直线平行,内错角相等.
19.56
【分析】根据长方形的对边平行知AD∥BC,据此得∠DEF=∠EFB=62°,∠EGF=∠AEG再根据折叠变换的性质知∠GEF=∠DEF=62°,继而由∠AEG=180° ∠DEF ∠GEF可得答案.
【详解】解:由题意知AD∥BC,∠1=62°,
∴∠DEF=∠EFB=62°,∠EGF=∠AEG
根据折叠变换的性质知∠GEF=∠DEF=62°,
则∠AEG=180° ∠DEF ∠G′EF=56°,
∴∠EGF=56°
故答案为:56
【点睛】本题主要考查平行线的性质,解题的关键是掌握两直线平行内错角相等的性质、翻折变换的性质.
20.##35度
【分析】根据两直线平行内错角相等和含角的直角三角板的特点即可求解.
【详解】如图,根据题意可知,
∴,
∴.
故答案为:.
【点睛】本题主要考查平行线的性质.掌握两直线平行内错角相等是解题关键.
21.(1)见解析(2)35°
【分析】(1)由知∠1=∠DCF,则∠2=∠DCF,即可证明;
(2)由得∠B=90°-∠2=35°,再根据(1)可知的度数.
【详解】∵
∴∠1=∠DCF,
∵
∴∠2=∠DCF,
∴;
(2)∵,∴∠BEF=90°,
∴∠B=90°-∠2=35°,
又∵
∴=∠B=35°.
【点睛】此题主要考查平行线的性质与判定.
22.∠AOC=115°,∠EOD=25°
【分析】由OF⊥CD,得∠DOF =90°,根据条件可求出∠BOD的度数,即可得到∠AOC的度数;由OE⊥AB,得∠BOE =90°,可以推出∠EOF和∠EOD的度数.
【详解】解:∵OF⊥CD,
∴∠DOF=90°,
又∵∠BOF=25°,
∴∠BOD=∠DOF+∠BOF=90°+25°=115°,
∴∠AOC=∠BOD=115°,
又∵OE⊥AB,
∴∠BOE=90°,
∵∠BOF=25°,
∴∠EOF=∠BOE -∠BOF =65°,
∴∠EOD=∠DOF﹣∠EOF=90°-65°=25°.
【点睛】此题考查的知识点是垂线、角的计算及对顶角知识,关键是根据垂线的定义得出所求角与已知角的关系.
23.(1)证明见解析;(2)105°
【分析】(1)首先根据角平分线的性质可得∠1=45°,再有∠3=45°,再根据内错角相等两直线平行可判定出AB∥CF;
(2)利用三角形内角和定理进行计算即可.
【详解】解:(1)证明:∵CF平分∠DCE,
∴∠1=∠2=∠DCE.
∵∠DCE=90°,
∴∠1=45°.
∵∠3=45°,
∴∠1=∠3.
∴AB∥CF.
(2)∵∠D=30°,∠1=45°,
∴∠DFC=180°﹣30°﹣45°=105°.
【点睛】本题考查平行线的判定,角平分线的定义及三角形内角和定理,熟练掌握相关性质定理是本题的解题关键.
24.(1)35°;
(2)36°;
【分析】(1)根据角平分线的定义和对顶角相等计算求值即可;
(2)由∠EOC+∠EOD=180°和∠EOC=∠EOD求得∠EOC,再结合(1)解答计算求值即可;
【详解】(1)解: ∵OA平分∠EOC,
∴∠AOC=∠EOC,
∵∠EOC=70°,
∴∠AOC=×70°=35°,
∵直线AB、CD相交于点O,
∴∠BOD=∠AOC=35°;
(2)解:∵∠EOC=∠EOD,∠EOC+∠EOD=180°,
∴∠EOD +∠EOD=180°,
∴∠EOD =180°,
∴∠EOD =108°,
∴∠EOC=×108°=72°,
∵OA平分∠EOC,
∴∠AOC=∠EOC=×72°=36°,
∵直线AB、CD相交于点O,
∴∠BOD=∠AOC=36°;
【点睛】本题考查了相交线,与角平分线有关的角的计算,补角的定义;掌握对顶角的性质是解题关键.
25.见解析
【分析】过点E作EF∥CD,根据平行线的性质即可得出∠B=∠BOD,根据平行线的性质即可得出∠BOD=∠BEF、∠D=∠DEF,结合角之间的关系即可得出结论.
【详解】证明:过点E作EF∥CD,如图
∵AB∥CD,
∴∠B=∠BOD,
∵EF∥CD(辅助线),
∴∠BOD=∠BEF(两直线平行,同位角相等);∠D=∠DEF(两直线平行,内错角相等);
∴∠BEF=∠BED+∠DEF=∠BED+∠D(等量代换),
∴∠BOD=∠E+∠D(等量代换), 即∠B=∠E+∠D.
【点睛】本题考查了平行线的性质以及角的计算,解题的关键是根据平行线的性质找出相等或互补的角.
26.(1)∠BOD,∠DOE;(2)160°
【分析】(1)分析图形,根据对顶角和补角的定义可以求出答案;
(2)先设∠COE=x求得∠COE和∠AOE的度数,再根据邻补角的定义求得∠AOD的度数,然后将∠AOE与∠AOD的度数相加即可.
【详解】解:(1)由图形可知,∠AOC的对顶角是∠BOD,∠COE的补角是∠DOE;
(2)设∠COE=x,则∠AOE=2x,
∵∠AOC=60°,
∴x+2x=60,
解得x=20,
即∠COE=20°,∠AOE=40°,
∵∠AOC+∠AOD=180°,
∴∠AOD=120°,
∴∠DOE=∠AOE+∠AOD=40°+120°=160°.
【点睛】本题考查角的运算,解题的关键是正确找出图中的角的等量关系,本题属于基础题型.
27.见解析
【分析】先利用平行线的性质与已知,说明∠ABC与∠EFC的关系,再利用平行线的判定方法说明AB与EF的关系,最后利用平行线的性质得结论.
【详解】证明:∵DE∥BC,
∴∠ADE=∠ABC.
∵∠ADE=∠EFC,
∴∠ABC=∠EFC.
∴AB∥EF.
∴∠1=∠2.
【点睛】本题考查了平行线的性质和判定,掌握“两直线平行,同位(内错)角相等”“同位角相等,两直线平行”是解决本题的关键.
28.(1)∠FOM,∠MOD,∠CON;(2)20°,70°
【分析】(1)根据垂直的定义可得∠BOF=∠AOF=90°,由角平分线的定义和对顶角相等可得与∠AON互余的角有:∠FOM,∠MOD,∠CON;
(2)设∠MOD的度数为x°,用含x的式子表示出∠FOD和∠AOC的度数,然后由∠AOC=∠BOD,得出∠FOD+∠AOC=90°,据此列方程求解,再由(1)中∠MOD与∠AON互余可得出∠AON的度数.
【详解】解:(1)∵FO⊥BO,∴∠BOF=∠AOF=90°,
∴∠BOM+∠FOM=90°,
又∠BOM=∠AON,∴∠AON+∠FOM=90°.
∵OM平分∠DOF,∴∠DOM=∠FOM,
又∵∠DOM=∠CON,
∴与∠AON互余的角有:∠FOM,∠MOD,∠CON;
(2)设∠MOD的度数为x°,
∵OM平分∠FOD,
∴∠MOD=∠FOM=x°,
∴∠FOD=2x°,∠AOC=∠FOM=°,
又∵FO⊥BO,∠AOC=∠BOD,
∴∠FOD+∠AOC=90°,
即2x+=90,
解得:x=20.
即∠MOD=20°,
由(1)可知∠MOD与∠AON互余,
∴∠AON=90°-∠MOD=90°-20°=70°.
故∠MOD的度数为20°,∠AON的度数为70°.
【点睛】本题考查了垂直的定义,角的平分线的定义,余角的定义与性质以及对顶角相等,正确理解相关概念是关键.
29.60°
【分析】由CD⊥AB,FE⊥AB,则,则∠2=∠4,从而证得,得∠B=∠ADG,则答案可解.
【详解】解:CD⊥AB于D,FE⊥AB于E,
∴,
∴∠2=∠4,
又∵∠1=∠2,
∴∠1=∠4,
∴,
∴.
【点睛】本题考查了平行线的判定和性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.
30.
【分析】根据题意,已知,,可结合平行线性质以及平角的定义即可求解.
【详解】解: ∵,,,
∴,
由折叠可知:,
∴.
【点睛】本题主要是考查了折叠的性质、平角的定义、平行线的性质;掌握以上知识点是解题的关键.
31.(1)115°;(2)45°
【分析】(1)根据角平分线的定义,得出∠EOC=∠BOE=65°,利用邻补角定义求出∠DOE即可;
(2)根据角平分线的定义,∠BOD:∠BOE=2:3,求出∠BOD,再根据对顶角可求出∠AOC,利用垂直,求出∠AOF.
【详解】(1)∵OE平分∠BOC,∠BOE=65°,
∴∠EOC=∠BOE=65°,
∴∠DOE=180°-∠EOC=180°-65°=115°;
(2)∵OE平分∠BOC,
∴∠EOC=∠BOE,
∵∠BOD:∠BOE=2:3,
设∠BOD=x,则∠COE=∠BOE=,
∵∠COE+∠BOE+∠BOD=180°,
∴,
∴x=45°,
∵OF⊥CD,∠BOD=∠AOC,
∴∠BOD=∠AOC=45°,
∴∠COF=90°,
∴∠AOF=∠COF-∠AOC=90°-45°=45°.
【点睛】本题考查了角平分线定义,邻补角定义,对顶角性质,垂直定义,角的计算等;正确找出各个角之间的关系是正确计算的关键.
32.(1)∠BOD =138°;(2)∠COE=21°.
【分析】(1)根据平角的定义即可得到结论;
(2)根据余角的性质得到∠COD=48°,根据角平分线的定义即可得到结论.
【详解】(1)∵A、O、B三点共线,∠AOD=42°,
∴∠BOD=180°﹣∠AOD=138°;
(2)∵∠COB=90°,
∴∠AOC=90°,
∵∠AOD=42°,
∴∠COD=48°,
∵OE平分∠BOD,
∴∠DOE=∠BOD=69°,
∴∠COE=69°﹣48°=21°.
【点睛】本题考查了余角和补角的知识,属于基础题,互余的两角之和为90°,互补的两角之和为180°是需要同学们熟练掌握的内容.
33.(1)证明见解析;(2)72°.
【分析】根据平行线的性质推出∠1=∠ACD,求出∠2=∠ACD,根据∠2+∠CAF=∠ACD+∠CAF推出∠DAC=∠4,求出∠DAC=∠3,根据平行线的判定得出即可.根据平行线性质可求得∠D=∠DCE.
【详解】(1)证明:∵AB∥CD,
∴∠1=∠ACD,
∵∠BCD=∠4+∠E,
∵∠3=∠4,
∴∠1=∠E,
∵∠1=∠2,
∴∠2=∠E,
∴AD∥BE;
(2)解:∵∠B=∠3=2∠2,∠1=∠2,
∴∠B=∠3=2∠1,
∵∠B+∠3+∠1=180°,
即2∠1+2∠1+∠1=180°,解得∠1=36°,
∴∠B=2∠1=72°,
∵AB∥CD,
∴∠DCE=∠B=72°,
∵AD∥BE,
∴∠D=∠DCE=72°.
【点睛】本题考查了平行线的性质和判定,三角形的外角性质的应用,能推出∠4=∠DAC=∠3是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.
34.135°
【分析】直接利用角平分线的定义得出,进而得出答案.
【详解】解:∵点A、O、B在一条直线上,∠COD=90°,
∴∠AOC+∠BOD=90°,
∵OE平分∠AOC,OF平分∠BOD,
∴∠AOE=∠COE=∠AOC,
∠DOF=∠BOF=∠DOB,
∴∠COE+∠DOF=×90°=45°,
∴∠EOF的度数为:90°+45°=135°.
【点睛】此题主要考查了角的计算以及角平分线的定义,正确得出∠COE+∠DOF=45°是解题关键.
35.(1)∠AOM=45°;(2)∠AOM=2∠NOC.理由见解析.
【分析】(1)根据互余、互补、角平分线的意义,得出各个角之间的关系,从而求出答案;
(2)设未知数,表示图中的各个角,再利用互补得出结论.
【详解】解:(1),平分,
,
,
,
,
,
;
(2).
令为,为,,
,
,
,即,
.
【点睛】考查角平分线的意义、互补、互余的意义,正确表示各个角,理清各个角之间的关系是得出正确结论的关键.
36.(1)、;(2);(3)见解析.
【分析】(1)根据余角的定义可解答;
(2)根据补角的定义列方程可解答;
(3)设出∠AOE的度数,依次表达图中的补角,可解.
【详解】(1)由题意可得于∠AOE互余的角为:、
(2)设.
∵,
∴,
.
∵,
∴.
又∵,
∴,即.
∴.
(3)设∠AOE=α,且0°<α<90°由(1)可知,∠AOD=∠BOC=90°-α,∠BOE=180°-α,
∴∠BOD=180°-∠AOD=180°-(90°-α)=90°+α,
∵OF平分∠BOD,
∴∠BOF=∠DOF=45°+,
∴∠AOF=∠AOD+∠DOF=90°-α+45°+=135°-,
∠EOF=∠AOF+∠AOE=135°+,
∠COF=∠BOC+∠BOF=90°-α+45°+=135°-=∠AOF,
①当∠AOF+∠AOE=180°时,即135°-+α=180°,解得α=90°,不符合题意;
②当∠EOF+∠AOE=180°时,即135°++α=180°,解得α=30°,符合题意;
③当∠BOD+∠AOE=180°时,即90°+α+α=180°,解得α=45°,符合题意;
综上可知,
当锐角时,互补角有2个,为、.
当锐角时,互补角有3个,为、、.
当锐角不等于和时,互补角有1个,为.
【点睛】本题主要考查补角的定义,角平分线的定义,熟练掌握补角的定义是解题关键.
37.(1)180°;(2)360°;(3)540°;(4)(n﹣1)180°
【详解】(1)
故答案为:180°,
(2)作
故答案为:360°;
(3)过E作EM∥AB,过F作FN∥AB,
∵AB∥CD,
∴AB∥EM∥FN∥CD,
∴∠1+∠AEM=180°,∠MEF+∠EFN=180°,∠NFC+∠4=180°,
∴∠1+∠AEF+∠EFC+∠4=3×180°=540°,
故答案为:540°;
(4)根据(1)(2)(3)的结果可知:∠1+∠2+∠3+∠4+…+∠n=180(n-1)°,
故答案为:180(n-1)°.
38.(1)∠CPD=∠α+∠β,理由见解析;(2)①当点P在A、M两点之间时,∠CPD=∠β ∠α;②当点P在B、O两点之间时,∠CPD=∠α ∠β
【分析】(1)过点P作PE∥AD交CD于点E,根据题意得出AD∥PE∥BC,从而利用平行线性质可知=∠DPE,=∠CPE,据此进一步证明即可;
(2)根据题意分当点P在A、M两点之间时以及当点P在B、O两点之间时两种情况逐一分析讨论即可.
【详解】(1)∠CPD=,理由如下:
如图3,过点P作PEAD交CD于点E,
∵ADBC,PEAD
∴ADPEBC
∴=∠DPE,=∠CPE
∴∠CPD=∠DPE+∠CPE=;
(2)①当点P在A、M两点之间时,∠CPD=,理由如下:
如图4,过点P作PEAD交CD于点E
∵ADBC,PEAD
∴ADPEBC
∴=∠EPD,=∠CPE
∴∠CPD=∠CPE ∠EPD=;
②当点P在B、O两点之间时,∠CPD=,理由如下:
如图5,过点P作PEAD交CD于点E
∵ADBC,PEAD
∴ADPEBC
∴=∠DPE,=∠CPE
∴∠CPD=∠DPE ∠CPE=
综上所述,当点P在A、M两点之间时,∠CPD=∠β ∠α;当点P在B、O两点之间时,∠CPD=∠α ∠β.
【点睛】本题主要考查了在平行线性质及判定的综合运用,熟练掌握相关概念是解题关键.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
