【解析版】北京市朝阳区2014届高三上学期期末考试 数学(理)试题
文档属性
| 名称 | 【解析版】北京市朝阳区2014届高三上学期期末考试 数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 547.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-07 08:15:41 | ||
图片预览



文档简介
(考试时间120分钟 满分150分)
本试卷分为选择题(共40分)和非选择题(共110分)两部分
第一部分(选择题 共40分)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个项中,选出符合题目要求的一项.
1.函数的定义域为( )
A. B. C. D.
2.如果点在以点为焦点的抛物线上,则( )
A. B. C. D.
3.命题:;命题:,,则下列命题中为真命题的是( )
A. B.
C. D.
4.在△中,,,,则△的面积等于( )
A. B.
C.或 D.或
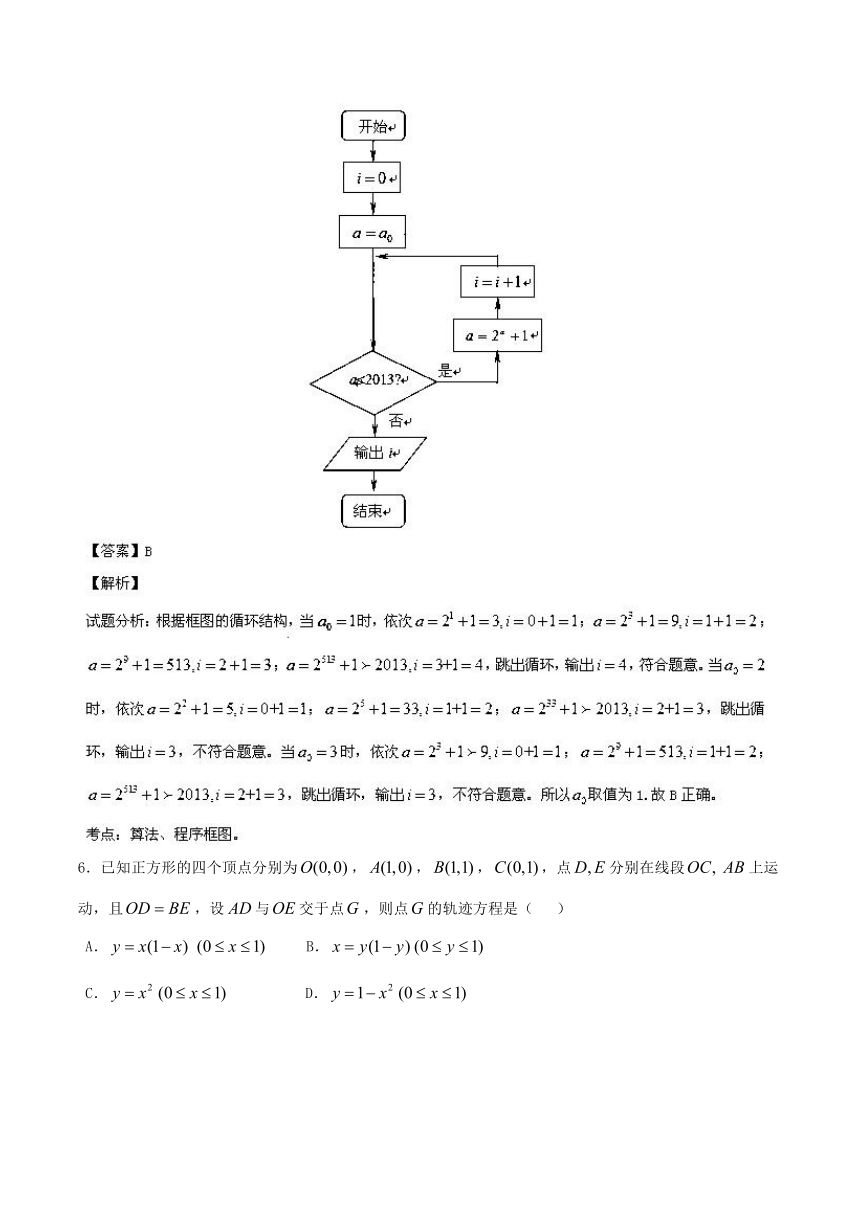
5.执行如图所示的程序框图,输出结果是.若,则所有可能的取值为( )
A. B.
C. D.
6.已知正方形的四个顶点分别为,,,,点分别在线段上运动,且,设与交于点,则点的轨迹方程是( )
A. B.
C. D.
7.已知平面向量,的夹角为,且,则的最小值为( )
A. B. C. D. 1
8.已知数列满足下面说法正确的是( )
①当时,数列为递减数列;
②当时,数列不一定有最大项;
③当时,数列为递减数列;
④当为正整数时,数列必有两项相等的最大项.
A. ①② B. ②④ C. ③④ D. ②③
第二部分(非选择题 共110分)
二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.
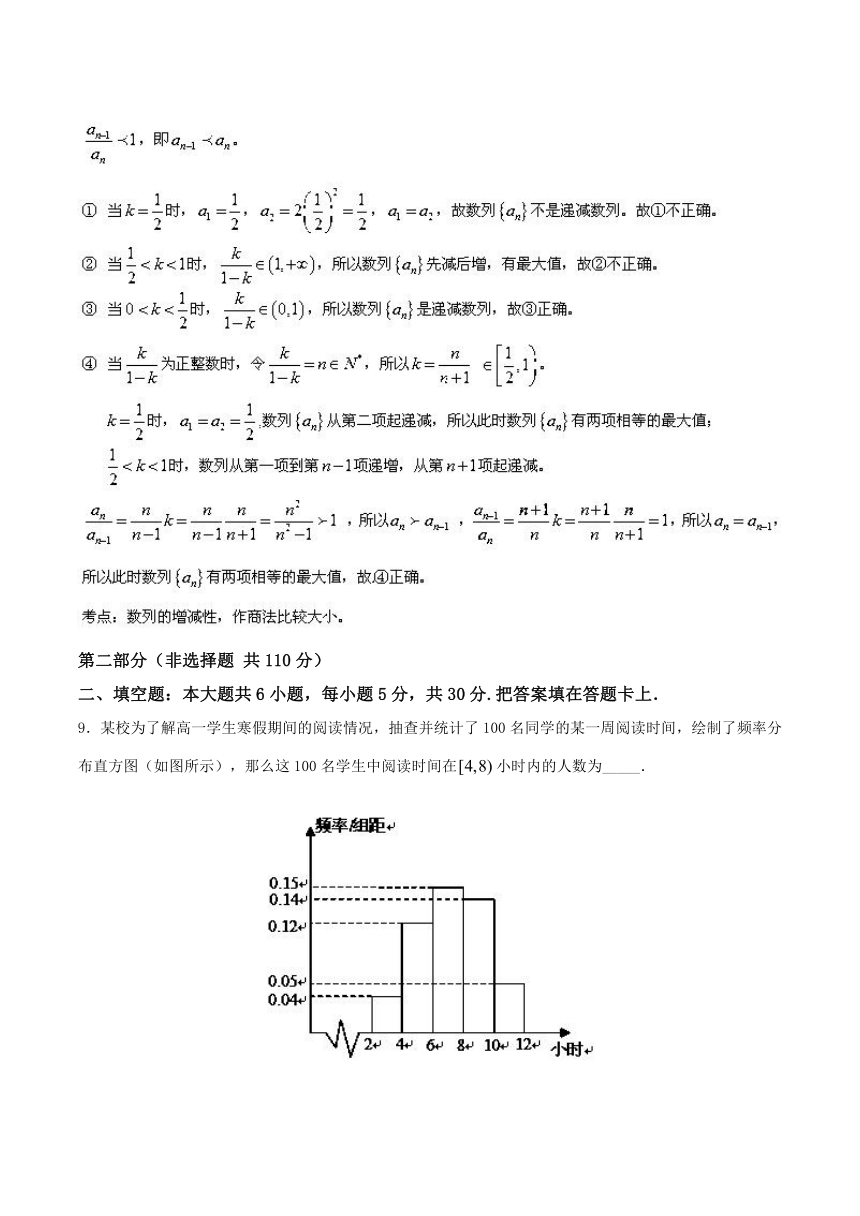
9.某校为了解高一学生寒假期间的阅读情况,抽查并统计了100名同学的某一周阅读时间,绘制了频率分布直方图(如图所示),那么这100名学生中阅读时间在小时内的人数为_____.
10.在各项均为正数的等比数列中,若,则 .
11.直线与圆相交于,两点,若,则实数的值
是_____.
12.一个三棱锥的三视图如图所示,则该三棱锥的体积是 ;表面积是 .
13.实数满足若恒成立,则实数的最大值是 .
【答案】
14.所有真约数(除本身之外的正约数)的和等于它本身的正整数叫做完全数.
如:;
;
.
已经证明:若是质数,则是完全数,.请写出一个四位完全数 ;又,所以的所有正约数之和可表示为;
,所以的所有正约数之和可表示为;
按此规律,的所有正约数之和可表示为 .
三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.
15.(本题满分13分)
已知函数.
(Ⅰ)求函数的最小值;
(Ⅱ)若,求的值.
16.(本题满分13分)
甲、乙两名同学参加“汉字听写大赛”选拔测试,在相同测试条件下,两人5次测试的成绩(单位:分)如下表:
(Ⅰ)请画出甲、乙两人成绩的茎叶图. 你认为选派谁参赛更好?说明理由(不用计算);
(Ⅱ)若从甲、乙两人5次的成绩中各随机抽取一个成绩进行分析,设抽到的两个成绩中,90分以上的个数为,求随机变量的分布列和期望.
17.(本题满分14分)
如图,在三棱锥中,平面,.
(Ⅰ)求证:;
(Ⅱ)设分别为的中点,点为△内一点,且满足,
求证:∥面;
(Ⅲ)若,,求二面角的余弦值.
即
不妨设,则有,所以.
因为,
(Ⅲ)由(Ⅱ)可知平面的一个法向量.
18.(本题满分13分)
已知函数,.
(Ⅰ)当时,求函数的极小值;
(Ⅱ)若函数在上为增函数,求的取值范围.
19. 已知椭圆两焦点坐标分别为,,且经过点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)已知点,直线与椭圆交于两点.若△是以为直角顶点的等腰直角三角形,试求直线的方程.
,
20.(本题满分13分)
已知是正数, ,,.
(Ⅰ)若成等差数列,比较与的大小;
(Ⅱ)若,则三个数中,哪个数最大,请说明理由;
(Ⅲ)若,,(),且,,的整数部分分别是求所有的值.
所以.
同课章节目录
