冀教版九年级下册30.5二次函数与一元二次方程的关系综合练习(无答案)
文档属性
| 名称 | 冀教版九年级下册30.5二次函数与一元二次方程的关系综合练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 423.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 00:00:00 | ||
图片预览



文档简介
30.5二次函数与一元二次方程的关系综合练习
班级:________ 姓名:________
一、单选题(共 10 小题)
1、已知二次函数y=x2+6x+c的图象与x轴的一个交点为(﹣1,0),则它与x轴的另一个交点的坐标是( )
A.(﹣3,0) B.(3,0) C.(﹣5,0) D.(5,0)
2、已知抛物线与轴的交点为和,点,是抛物线上不同于,的两个点,记的面积为,的面积为,有下列结论:
①当时,;
②当时,;
③当时,;
④当时,.
其中正确结论的序号是( )
A.②③ B.①③ C.①②③④ D.③
3、已知二次函数y=ax2+bx+c(a≠0)的顶点坐标(﹣1,﹣3.2)及部分图象(如图),由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=1.3和x2=( )
A.﹣1.3 B.﹣2.3 C.﹣0.3 D.﹣3.3
4、已知二次函数y=ax2 4ax 5a+1(a>0)下列结论正确的是( )
①已知点M(4,y1),点N( 2,y2)在二次函数的图象上,则y1>y2;
②该图象一定过定点(5,1)和(-1,1);
③直线y=x 1与抛物线y=ax2 4ax 5a+1一定存在两个交点;
④当 3≤x≤1时,y的最小值是a,则a=
A.①④ B.②③ C.②④ D.①②③④
5、如图,二次函数y=ax2+bx(a≠0)的图像过点(2,0),下列结论错误的是( )
A.b>0
B.a+b>0
C.x=2是关于x的方程ax2+bx=0(a≠0)的一个根
D.点(x1,y1),(x2,y2)在二次函数的图像上,当x1>x2>2时,y2<y1<0
6、如图,点A是抛物线图象在第一象限内的一个动点,且点A的横坐标大于1,点E的坐标是(0,1),过点A作AB轴交抛物线于点B,过A、B作直线AE、BE分别交轴于点D、C,设阴影部分的面积为,点A的横坐标为,则关于的函数关系式为( )
A. B. C. D.
7、满足的所有实数对,使取最小值,此最小值为( )
A. B. C. D.
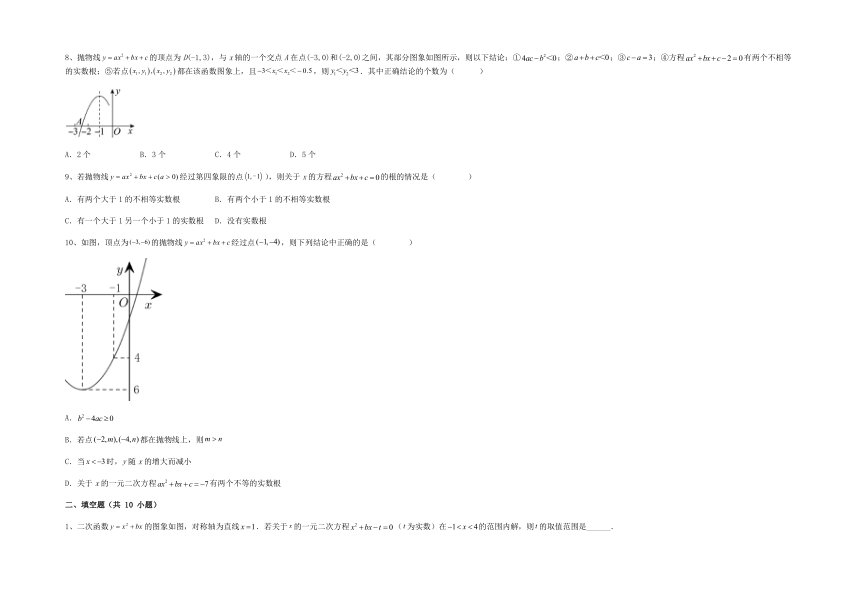
8、抛物线的顶点为D(-1,3),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图所示,则以下结论:①;②;③;④方程有两个不相等的实数根;⑤若点都在该函数图象上,且,则.其中正确结论的个数为( )
A.2个 B.3个 C.4个 D.5个
9、若抛物线经过第四象限的点),则关于x的方程的根的情况是( )
A.有两个大于1的不相等实数根 B.有两个小于1的不相等实数根
C.有一个大于1另一个小于1的实数根 D.没有实数根
10、如图,顶点为的抛物线经过点,则下列结论中正确的是( )
A.
B.若点都在抛物线上,则
C.当时,y随x的增大而减小
D.关于x的一元二次方程有两个不等的实数根
二、填空题(共 10 小题)
1、二次函数的图象如图,对称轴为直线.若关于的一元二次方程(为实数)在的范围内解,则的取值范围是______.
2、如图,抛物线,直线与抛物线、轴分别相交于点、.
(1)当时,点的坐标为______;
(2)当时,在拋物线与轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,此时“可点”的个数为______.
3、已知关于x的一元二次方程的两个根为、()则实数,,,的大小关系为:________________.
4、下列关于抛物线为常数,且的四个结论:
①若,则抛物线与直线没有公共点;
②若,则当时,随的增大而减小;
③若抛物线与轴有两个交点,则其中一定有一个交点在点与之间;
④当的值变化时,抛物线的顶点始终在同一条直线上.
其中正确的结论是______填写序号.
5、已知二次函数与一次函数的图象相交于点和,如图所示,则使不等式成立的的取值范围是_____________.
6、抛物线y=ax2+bx+c(a,b,c为常数)的部分图象如图所示,设m=a-b+c,则m的取值范围是______.
7、已知抛物线与轴的一个交点为,则代数式的值为________.
8、已知抛物线与x轴的两个交点的横坐标分别是-3和1,若抛物线与x轴有两个交点A,B,点A的坐标是,则点B的坐标是______.
9、抛物线上部分点的对应值如下表:
x … 0 1 2 …
y … 0 4 6 6 4 …
从上表可知,下列说法中正确的是 _____(填序号).
①抛物线与x轴的一个交点为 ;
②抛物线的对称轴是直线;
③函数的最大值是6;
④在对称轴的左侧,y随x的增大而增大.
10、二次函数的图像如图所示,则下列结论:① abc<0;②③④⑤对称轴为,其中正确结的确序号是_____.
三、解答题(共 6 小题)
1、抛物线y=﹣x2+bx+c经过点A(﹣3,0)和点C(0,3).
(1)求此抛物线所对应的函数解析式,并直接写出顶点D的坐标;
(2)若过顶点D的直线将△ACD的面积分为1:2两部分,并与x轴交于点Q,则点Q的坐标为 .
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标()
2、如图,抛物线与x轴交于点A(-2,0)和点B(4,0),与y轴交于点C(0,4)
(1)求抛物线的解析式.
(2)点D在抛物线的对称轴上,求AD+CD的最小值.
(3)点P是直线BC上方的点,连接CP,BP,若△BCP的面积等于3,求点P的坐标.
3、如图,抛物线与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.已知A(-1,0),C(0,3).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点M,使得的值最大,求此点M的坐标;
(3)在抛物线的对称轴上是否存在P点,使△PCD是等腰三角形,如果存在,求出点P的坐标,如果不存在,请说明理由.
4、已知抛物线的顶点为,与y轴交于点,点为其对称轴上的一个定点.
(1)求这条抛物线的函数解析式;
(2)已知直线l是过点且垂直于y轴的定直线,若抛物线上的任意一点到直线l的距离为d,求证:;
(3)已知坐标平面内的点,请在抛物线上找一点Q,使的周长最小,并求此时周长的最小值及点Q的坐标.
5、在平面直角坐标系中,点在抛物线上,设抛物线的对称轴为
(1)当时,求抛物线与y轴交点的坐标及的值;
(2)点在抛物线上,若求的取值范围及的取值范围.
6、如图,已知二次函数的图象与x轴交于A( 3,0)、B(1,0)两点,与y轴交于点C.
(1)求二次函数的解析式;
(2)当时,请直接写出x的范围;
(3)点D是抛物线上位于第二象限的一个动点,连接CD,当∠ACD=90°时,求点D的横坐标.
班级:________ 姓名:________
一、单选题(共 10 小题)
1、已知二次函数y=x2+6x+c的图象与x轴的一个交点为(﹣1,0),则它与x轴的另一个交点的坐标是( )
A.(﹣3,0) B.(3,0) C.(﹣5,0) D.(5,0)
2、已知抛物线与轴的交点为和,点,是抛物线上不同于,的两个点,记的面积为,的面积为,有下列结论:
①当时,;
②当时,;
③当时,;
④当时,.
其中正确结论的序号是( )
A.②③ B.①③ C.①②③④ D.③
3、已知二次函数y=ax2+bx+c(a≠0)的顶点坐标(﹣1,﹣3.2)及部分图象(如图),由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=1.3和x2=( )
A.﹣1.3 B.﹣2.3 C.﹣0.3 D.﹣3.3
4、已知二次函数y=ax2 4ax 5a+1(a>0)下列结论正确的是( )
①已知点M(4,y1),点N( 2,y2)在二次函数的图象上,则y1>y2;
②该图象一定过定点(5,1)和(-1,1);
③直线y=x 1与抛物线y=ax2 4ax 5a+1一定存在两个交点;
④当 3≤x≤1时,y的最小值是a,则a=
A.①④ B.②③ C.②④ D.①②③④
5、如图,二次函数y=ax2+bx(a≠0)的图像过点(2,0),下列结论错误的是( )
A.b>0
B.a+b>0
C.x=2是关于x的方程ax2+bx=0(a≠0)的一个根
D.点(x1,y1),(x2,y2)在二次函数的图像上,当x1>x2>2时,y2<y1<0
6、如图,点A是抛物线图象在第一象限内的一个动点,且点A的横坐标大于1,点E的坐标是(0,1),过点A作AB轴交抛物线于点B,过A、B作直线AE、BE分别交轴于点D、C,设阴影部分的面积为,点A的横坐标为,则关于的函数关系式为( )
A. B. C. D.
7、满足的所有实数对,使取最小值,此最小值为( )
A. B. C. D.
8、抛物线的顶点为D(-1,3),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图所示,则以下结论:①;②;③;④方程有两个不相等的实数根;⑤若点都在该函数图象上,且,则.其中正确结论的个数为( )
A.2个 B.3个 C.4个 D.5个
9、若抛物线经过第四象限的点),则关于x的方程的根的情况是( )
A.有两个大于1的不相等实数根 B.有两个小于1的不相等实数根
C.有一个大于1另一个小于1的实数根 D.没有实数根
10、如图,顶点为的抛物线经过点,则下列结论中正确的是( )
A.
B.若点都在抛物线上,则
C.当时,y随x的增大而减小
D.关于x的一元二次方程有两个不等的实数根
二、填空题(共 10 小题)
1、二次函数的图象如图,对称轴为直线.若关于的一元二次方程(为实数)在的范围内解,则的取值范围是______.
2、如图,抛物线,直线与抛物线、轴分别相交于点、.
(1)当时,点的坐标为______;
(2)当时,在拋物线与轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,此时“可点”的个数为______.
3、已知关于x的一元二次方程的两个根为、()则实数,,,的大小关系为:________________.
4、下列关于抛物线为常数,且的四个结论:
①若,则抛物线与直线没有公共点;
②若,则当时,随的增大而减小;
③若抛物线与轴有两个交点,则其中一定有一个交点在点与之间;
④当的值变化时,抛物线的顶点始终在同一条直线上.
其中正确的结论是______填写序号.
5、已知二次函数与一次函数的图象相交于点和,如图所示,则使不等式成立的的取值范围是_____________.
6、抛物线y=ax2+bx+c(a,b,c为常数)的部分图象如图所示,设m=a-b+c,则m的取值范围是______.
7、已知抛物线与轴的一个交点为,则代数式的值为________.
8、已知抛物线与x轴的两个交点的横坐标分别是-3和1,若抛物线与x轴有两个交点A,B,点A的坐标是,则点B的坐标是______.
9、抛物线上部分点的对应值如下表:
x … 0 1 2 …
y … 0 4 6 6 4 …
从上表可知,下列说法中正确的是 _____(填序号).
①抛物线与x轴的一个交点为 ;
②抛物线的对称轴是直线;
③函数的最大值是6;
④在对称轴的左侧,y随x的增大而增大.
10、二次函数的图像如图所示,则下列结论:① abc<0;②③④⑤对称轴为,其中正确结的确序号是_____.
三、解答题(共 6 小题)
1、抛物线y=﹣x2+bx+c经过点A(﹣3,0)和点C(0,3).
(1)求此抛物线所对应的函数解析式,并直接写出顶点D的坐标;
(2)若过顶点D的直线将△ACD的面积分为1:2两部分,并与x轴交于点Q,则点Q的坐标为 .
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标()
2、如图,抛物线与x轴交于点A(-2,0)和点B(4,0),与y轴交于点C(0,4)
(1)求抛物线的解析式.
(2)点D在抛物线的对称轴上,求AD+CD的最小值.
(3)点P是直线BC上方的点,连接CP,BP,若△BCP的面积等于3,求点P的坐标.
3、如图,抛物线与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.已知A(-1,0),C(0,3).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点M,使得的值最大,求此点M的坐标;
(3)在抛物线的对称轴上是否存在P点,使△PCD是等腰三角形,如果存在,求出点P的坐标,如果不存在,请说明理由.
4、已知抛物线的顶点为,与y轴交于点,点为其对称轴上的一个定点.
(1)求这条抛物线的函数解析式;
(2)已知直线l是过点且垂直于y轴的定直线,若抛物线上的任意一点到直线l的距离为d,求证:;
(3)已知坐标平面内的点,请在抛物线上找一点Q,使的周长最小,并求此时周长的最小值及点Q的坐标.
5、在平面直角坐标系中,点在抛物线上,设抛物线的对称轴为
(1)当时,求抛物线与y轴交点的坐标及的值;
(2)点在抛物线上,若求的取值范围及的取值范围.
6、如图,已知二次函数的图象与x轴交于A( 3,0)、B(1,0)两点,与y轴交于点C.
(1)求二次函数的解析式;
(2)当时,请直接写出x的范围;
(3)点D是抛物线上位于第二象限的一个动点,连接CD,当∠ACD=90°时,求点D的横坐标.
