3.4.2 简单机械（26张ppt）

(共34张PPT)
第二课时 杠杆平衡及分类
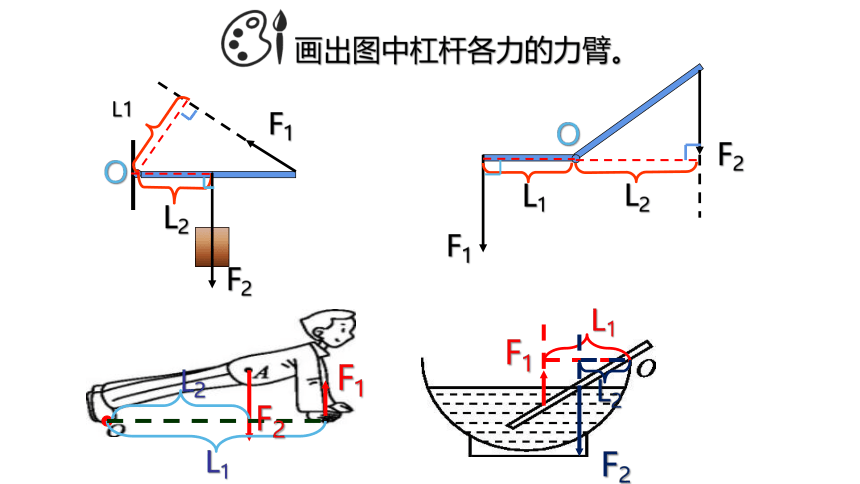
画出图中杠杆各力的力臂。
F1
F2
L1
L2
F1
F2
L1
O
L2
O
F1
L1
L2
F2
F1
F2
L1
L2
问题一：如何判断物体处于受力平衡？
物体在力的作用下处于静止或匀速直线运动状态
F支
G
∵ 物体静止
∴F支=G
F拉
f
∵ 物体匀速直线运动
∴F拉=f
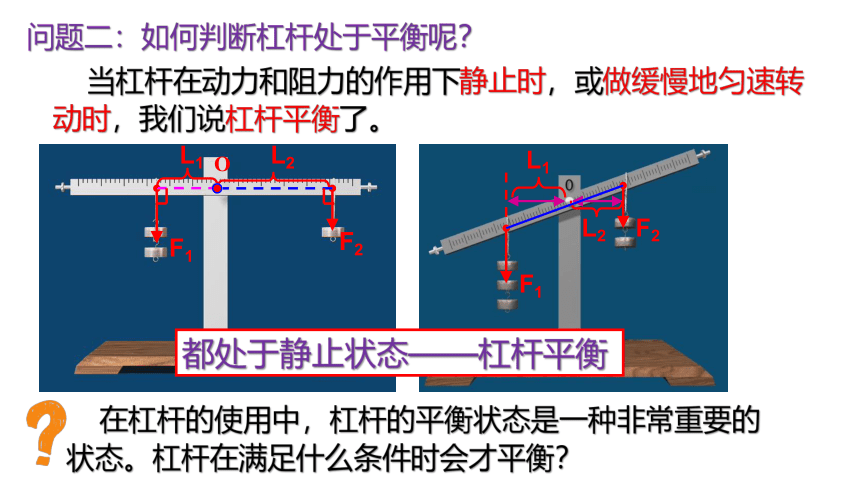
当杠杆在动力和阻力的作用下静止时，或做缓慢地匀速转动时，我们说杠杆平衡了。
在杠杆的使用中，杠杆的平衡状态是一种非常重要的状态。杠杆在满足什么条件时会才平衡？
问题二：如何判断杠杆处于平衡呢？
F1
F2
O
L2
L1
F1
F2
L2
L1
都处于静止状态——杠杆平衡
一、杠杆平衡的条件
提出问题：
杠杆平衡时，动力、动力臂、阻力、阻力臂之间存在着怎样的关系？
猜想与假设：
假设一：
假设二：
假设三：
假设四：
F1 + L1 = F2 + L2
F1 – L1 = F2 – L2
F1 / F2 = L1 / L2
F1 · L1 = F2 · L2
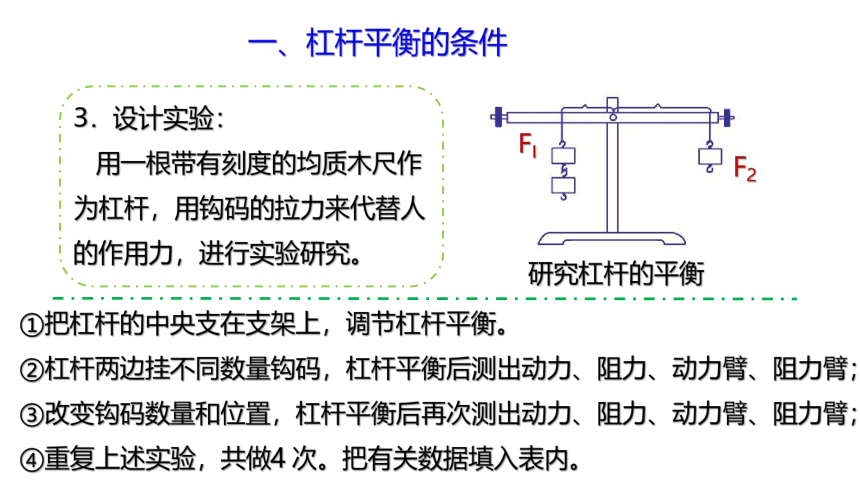
3．设计实验：
用一根带有刻度的均质木尺作为杠杆，用钩码的拉力来代替人的作用力，进行实验研究。
FI
F2
研究杠杆的平衡
一、杠杆平衡的条件
①把杠杆的中央支在支架上，调节杠杆平衡。
②杠杆两边挂不同数量钩码，杠杆平衡后测出动力、阻力、动力臂、阻力臂；
③改变钩码数量和位置，杠杆平衡后再次测出动力、阻力、动力臂、阻力臂；
④重复上述实验，共做4 次。把有关数据填入表内。
记录表
序号 动力F1（牛） 动力臂L1（厘米） 阻力F2（牛） 阻力臂L2（厘米）
1
2
3
4
4. 将动力F1、阻力F2、动力臂L1、阻力臂L2记录表格中。
F1×L1
F2×L2
×
×
=
5. 分析与论证：
分析实验数据，得出实验结论：____________________________________________________。
一、杠杆平衡的条件
杠杆的平衡条件是：动力乘以动力臂
等于阻力乘以阻力臂
或
F1
L1
F2
L2
=
即
F1
F2
=
L2
L1
L1
L2
=
若
n
则
F1
F2
=
1
n
杠杆上的动力臂是阻力臂的几倍，动力就是阻力的几分之一。
F1 × L1 =
F2 × L2
（1）调节平衡螺母，使杠杆水平平衡。
（2）杠杆两端挂上不同数量的钩码，移动钩码的位置，使杠杆水平平衡。
F1
F2
O
L2
L1
F1
F2
L2
L1
倾斜状态时力臂比杠杆上的刻度小
使杠杆的重力作用线通过杠杆支点，避免杠杆自身重力对杠杆平衡的影响。
要求杠杆静止时在水平位置，可以直接在杠杆上读出力臂的数值。
思考：为什么要调节杠杆在水平位置平衡，而不使它处于倾斜状态平衡
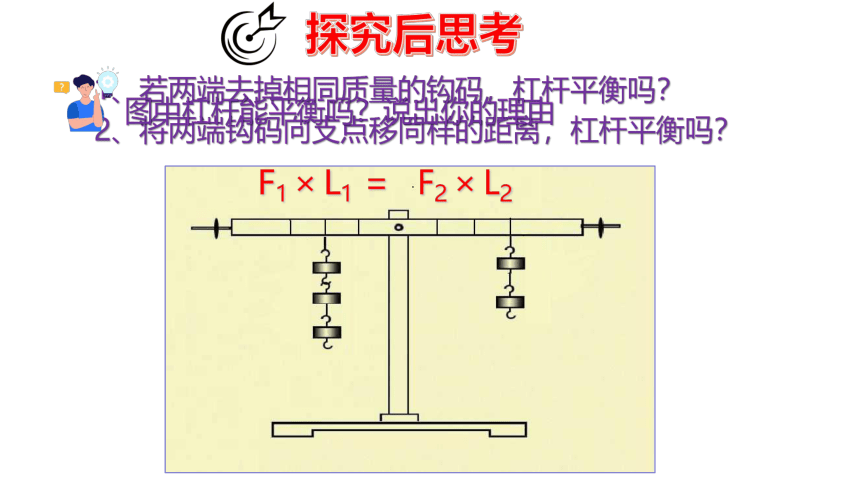
探究后思考
探究后思考
1、若两端去掉相同质量的钩码，杠杆平衡吗？
2、将两端钩码向支点移同样的距离，杠杆平衡吗？
图中杠杆能平衡吗？说出你的理由
F1 × L1 =
F2 × L2
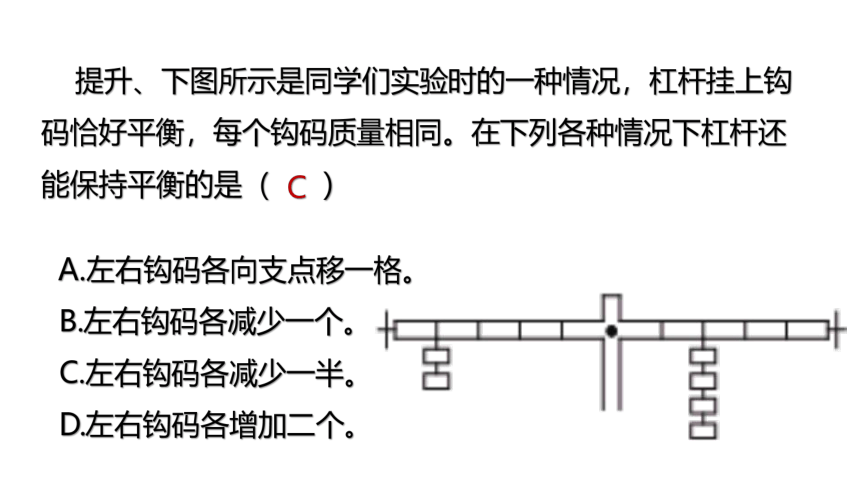
提升、下图所示是同学们实验时的一种情况，杠杆挂上钩码恰好平衡，每个钩码质量相同。在下列各种情况下杠杆还能保持平衡的是（ ）
A.左右钩码各向支点移一格。
B.左右钩码各减少一个。
C.左右钩码各减少一半。
D.左右钩码各增加二个。
C
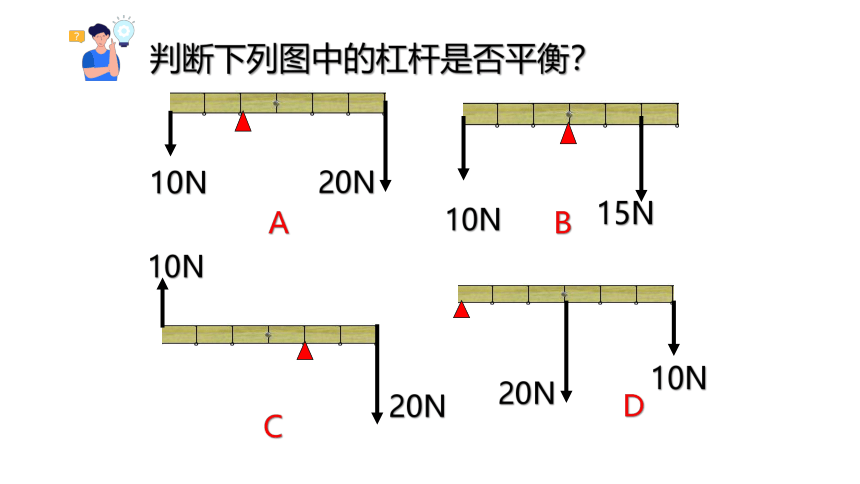
10N
20N
10N
15N
10N
20N
20N
10N
判断下列图中的杠杆是否平衡？
A
B
C
D
拓展
活动①：请你用弹簧测力计代替一侧钩码，使杠杆平衡，并读出此时的数据
F1
F2
F3
L3
L1
L2
活动②：如果将弹簧秤向右下方拉，读数发生怎样变化？
向左下方拉呢？
为什么
阻力和阻力臂不变，
L1最长，
F1最小。
思考：弹簧秤向哪个方向更省力
拓展
活动③：用弹簧测力计代替一侧钩码，向上拉能使杠杆平衡吗？请你试一试，并读出此时的数据
L＇
F1
L1
向斜上方拉呢？
阻力和阻力臂不变，
动力臂越短，
需要动力就越大
为什么斜向上拉费力
当堂练
例2 （2019 深圳）如右图所示，在C点用力把桌腿A抬离地面时，桌腿B始终没有移动，请在C点画出最小作用力的示意图。
以B为支点
最长力臂为BC
最小的力与BC垂直
F
例3 （2019 青岛）如图为探究杠杆平衡条件的实验装置，杠杆平衡时，钩码对杠杆的阻力F2=10N，阻力臂l2=20cm，测力计示数F1=25N，则动力臂l1为（　　）
A．15cm B．8cm
C．50cm D．80cm
B
解析：根据杠杆的平衡条件F1l1=F2l2
得动力臂：
【例题】如图是铁道检修工用的道钉撬，有关尺寸见图。若在A点竖直向下作用200 牛的力，道钉撬对道钉会产生多大的力？如果还不能将道钉撬出，在保持手的作用力大小和作用点不变的情况下，采用什么方法可增大道钉撬对道钉的作用力？
解：据杠杆平衡条件 F1l1 = F2l2，
可得：F2 = F1l1/l2
= 200牛×120 厘米/6 厘米
= 4000 牛
答：道钉撬对道钉能产生4000 牛的力。将F1 的方向与撬棒垂直，可增大撬棒对道钉的作用力。
巩固：用铁锤拔钉的情景如图所示，由图中所提供的数据，求出钉子对铁锤的阻力。
解：据杠杆平衡条件 F1l1 = F2l2，
可得：F2 = F1l1/l2
= 50牛×20 厘米/2 厘米
= 500 牛
答：钉子对铁锤的阻力500 牛。
手握处离支点近些还是远些更省力
G
提升：如图提升重物G，作用在杠杆一端且始终与杠杆垂直的力F，将杠杆缓慢地由位置A拉至水平位置B，力F在这个过程中（ ）
A．变大 B．变小
C．不变 D．先变大后变小
O
A
F
B
G
F'
由F1 l1 = F2 l2
因 l1 不变； F2不变
由于 l2变大；所以F1变大
l2
l2'
A
G
B
A
F
O
如图所示，用轻质杠杆把重物匀速提升的过程中，力F方向始终跟杠杆垂直，那么力F的大小（ ）
A.逐渐变小
B.逐渐变大
C.保持不变
D.先变大后变小
G
A
F1 × L1 = F2 × L2
不变
不变
变小
竖直向上
变小
不变
变小
F
力臂之比不变
不变
homework
1.作业本A.P39-40；
2.练习卷一张3.4 第二课时（A组全做，B组做9，11）
3.订正练习卷第一课时（共享文件夹）
二、杠杆的类型
杠杆类型 杠杆特点 杠杆优点 杠杆缺点 应 用
省力杠杆
费力杠杆
等臂杠杆
L1>L2
F1(动力<阻力)
L1F1>F2
(动力>阻力)
L1=L2
F1=F2
(动力=阻力)
省力
费距离
省距离
费力
既不省力也不省距离
若克服的阻力较小时，要用费力杠杆。
使用费力杠杆，可以省距离。
能使工作快捷。
费力杠杆
O
F1
F2
l2
l1
O
F1
F2
S1
S2
若克服的阻力较大时，要用省力杠杆。
省力杠杆
等臂杠杆
F1
F2
L1
L2
O
L1
L2
=
跷
跷
板
费力杠杆
省力杠杆
费力杠杆
费力杠杆
省力杠杆
费力杠杆
省力杠杆
省力杠杆
省力杠杆
费力杠杆
省力杠杆
当堂练
例1（2019 河南）如图开瓶器开启瓶盖时可抽象为一杠杆，不计自重。下图能正确表示它工作示意图的是（　　）
A B
C D
支点
动力
阻力
O
F1
F2
B
例2（2019 北京）如图所示的用具中，在使用时属于费力杠杆的是（　　）
A．筷子 B．瓶盖起子 C．撬棒 D．核桃夹
A
徒手无法完成，要用省力杠杆
3. 各式各样的剪刀都是一对对杠杆。下列剪刀，最适合剪开较硬物体的是 （　　）
A B C D
C
homework
1.作业本B.P39-40；
2.练习卷一张3.4 第三课时（A组）
3.订正练习卷第二课时（共享文件夹）
4.回顾期中卷错题