【模块四 三角形】专题1 线与角-2023年中考数学第一轮复习(含解析)
文档属性
| 名称 | 【模块四 三角形】专题1 线与角-2023年中考数学第一轮复习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-03 06:32:33 | ||
图片预览




文档简介
2023年中考数学第一轮复习
模块四 三角形
专题1 线与角
线与角 线 直线 经过两点有且只有一条直线.直线是向两方无限延伸的,直线没有端点.
射线 直线上一点和它一旁的部分叫做射线,这点叫做射线的端点,射线向一方无限延伸,射线只有一个端点.
线段 1、直线上两个点和它们之间的部分叫做线段.线段有两个端点,有长短之分,将某一线段分成两条相等的线段的点叫做该线段的中点. 2、两点确定一条直线,两点之间线段最短,两点之间线段的长度叫做两点之间的距离.
角 角度换算 1°=60',1'=60″. 1周角=2平角=4直角=360°.
余角 如果两个角的和等于90°,就说这两个角互为余角; 同角或等角的余角相等.
补角 如果两个角的和等于180°,就说这两个角互为补角; 同角或等角补角相等.
对顶角 一个角的两边是另一个角的两边的反向延长线,则称这两个角是对顶角,对顶角相等.
角平分线 性质 角平分线上的点到角两边的距离相等
判定 到角两边距离相等的点在角平分线上.
线段垂直平分线 定义 垂直平分一条线段的直线叫做线段的垂直平分线.
性质 线段的垂直平分线上的点到这条线段两个端点的距离相等,
判定 到线段两端距离相等的点在线段的垂直平分线上.
垂线 在同一平面内,过一点有且只有一条直线与已知直线垂直. 垂线段公理:直线外一点与已知线段连接的所有线段中,垂线段最短.
平行线 过直线外一点,有且只有一条直线与这条直线平行.
性质 ① 两条直线平行,同位角相等; ② 两条直线平行,内错角相等; ③ 两条直线平行,同旁内角互补.
判定 ① 同位角相等,两条直线平行; ② 内错角相等,两条直线平行; ③ 同旁内角互补,两条直线平行.
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
题型一、线与角的有关概念
1.(2022 连云港)已知∠A的补角为60°,则∠A= .
2.(2022·北京)如图,利用工具测量角,则的大小为( )
A.30° B.60° C.120° D.150°
3.(2022·广西贺州)如图,在Rt△ABC中,∠C=90°,∠B=56°,则∠A的度数为( )
A. B. C. D.
4.(2022·河南)如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )
A.26° B.36° C.44° D.54°
5.(2022·广西)如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么∠BAC的大小为______
6.(2022·江苏苏州·中考真题)如图,直线AB与CD相交于点O,,,则的度数是( )
A.25° B.30° C.40° D.50°
题型二、相交线与平行线
1.(2022 广东)如图,直线a∥b,∠1=40°,则∠2=( )
A.30° B.40°
C.50° D.60°
2.(2022·甘肃兰州)如图,直线,直线c与直线a,b分别相交于点A,B,,垂足为C.若,则( )
A.52° B.45° C.38° D.26°
3.(2022·湖南郴州)如图,直线,且直线a,b被直线c,d所截,则下列条件不能判定直线的是( )
A. B. C. D.
4.(2022·内蒙古通辽)如图,一束光线先后经平面镜,反射后,反射光线与平行,当时,的度数为( )
A. B. C. D.
5.(2022·浙江绍兴·中考真题)如图,把一块三角板的直角顶点B放在直线上,,ACEF,则( )
A.30° B.45° C.60° D.75°
6.(2022·湖北鄂州)如图,直线l1l2,点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )
A.10° B.15° C.20° D.30°
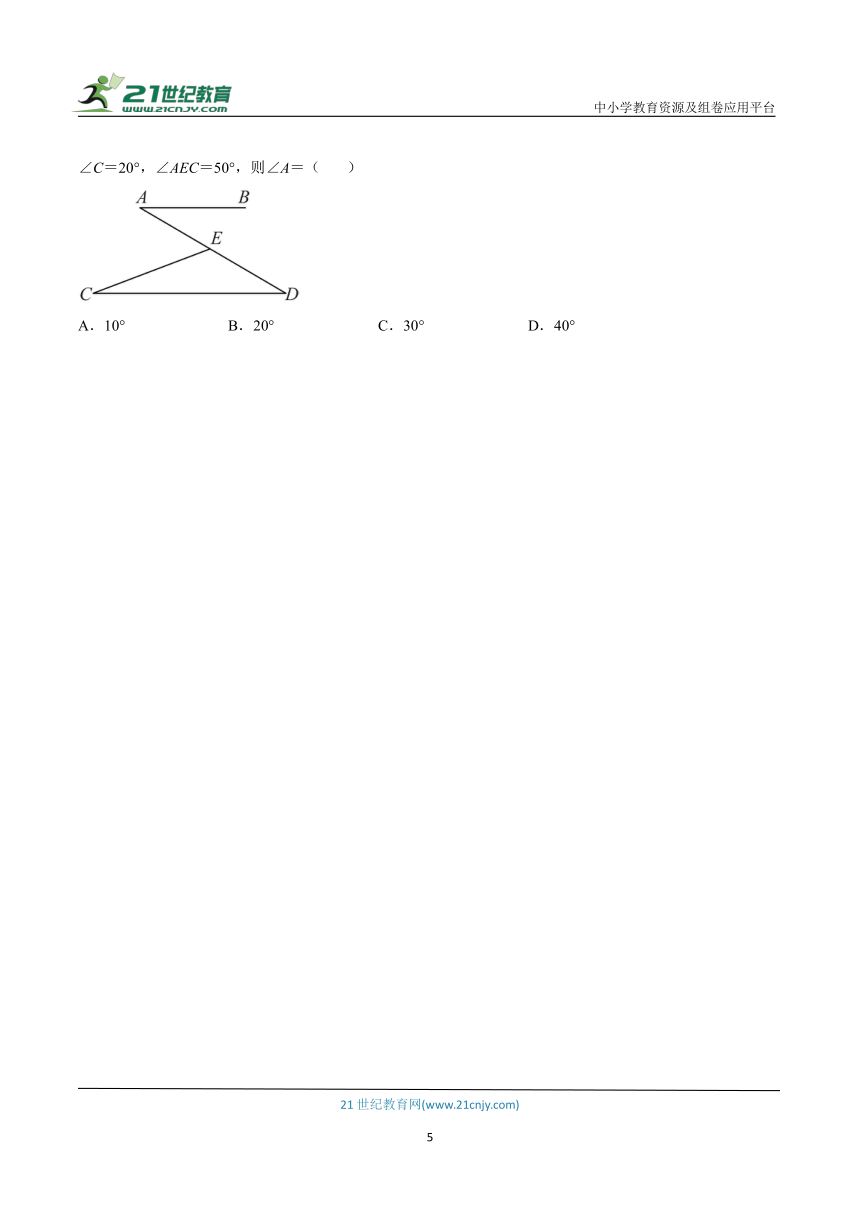
7.(2022·浙江杭州·中考真题)如图,已知,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10° B.20° C.30° D.40°
8.(2022·海南)如图,直线,是等边三角形,顶点B在直线n上,直线m交于点E,交于点F,若,则的度数是( )
A. B. C. D.
9.(2022·黑龙江齐齐哈尔)如图所示,直线a∥b,点A在直线a上,点B在直线b上,AC=BC,∠C=120°,∠1=43°,则∠2的度数为( )
A.57° B.63° C.67° D.73°
10.(2022·湖北恩施)已知直线,将含30°角的直角三角板按图所示摆放.若,则( )
A.120° B.130° C.140° D.150°
题型三、角平分线
1.(2021·湖南益阳)如图,与相交于点O,是的平分线,且恰好平分,则_______度.
2.(2022·湖南株洲·中考真题)如图所示,点在一块直角三角板上(其中),于点,于点,若,则_________度.
3.(2022·湖南郴州)如图.在中,,.以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于长为半径作弧,在内两弧相交于点P;作射线AP交BC于点F,过点F作,垂足用G.若,则的周长等于________cm.
题型四、线段的垂直平分线
1.(2022·湖北宜昌·中考真题)如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点,.作直线,交于点,交于点,连接.若,,,则的周长为( )
A.25 B.22 C.19 D.18
2.(2022·四川成都)如图,在中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交边于点.若,,,则的长为_________.
3.(2022·四川达州·中考真题)如图,在中,,,分别以点A,B为圆心,大于的长为半径作弧,两弧分别相交于点M,N,作直线,交于点D,连接,则的度数为_____.
2023年中考数学第一轮复习
模块四 三角形
专题1 线与角
线与角 线 直线 经过两点有且只有一条直线.直线是向两方无限延伸的,直线没有端点.
射线 直线上一点和它一旁的部分叫做射线,这点叫做射线的端点,射线向一方无限延伸,射线只有一个端点.
线段 1、直线上两个点和它们之间的部分叫做线段.线段有两个端点,有长短之分,将某一线段分成两条相等的线段的点叫做该线段的中点. 2、两点确定一条直线,两点之间线段最短,两点之间线段的长度叫做两点之间的距离.
角 角度换算 1°=60',1'=60″. 1周角=2平角=4直角=360°.
余角 如果两个角的和等于90°,就说这两个角互为余角; 同角或等角的余角相等.
补角 如果两个角的和等于180°,就说这两个角互为补角; 同角或等角补角相等.
对顶角 一个角的两边是另一个角的两边的反向延长线,则称这两个角是对顶角,对顶角相等.
角平分线 性质 角平分线上的点到角两边的距离相等
判定 到角两边距离相等的点在角平分线上.
线段垂直平分线 定义 垂直平分一条线段的直线叫做线段的垂直平分线.
性质 线段的垂直平分线上的点到这条线段两个端点的距离相等,
判定 到线段两端距离相等的点在线段的垂直平分线上.
垂线 在同一平面内,过一点有且只有一条直线与已知直线垂直. 垂线段公理:直线外一点与已知线段连接的所有线段中,垂线段最短.
平行线 过直线外一点,有且只有一条直线与这条直线平行.
性质 ① 两条直线平行,同位角相等; ② 两条直线平行,内错角相等; ③ 两条直线平行,同旁内角互补.
判定 ① 同位角相等,两条直线平行; ② 内错角相等,两条直线平行; ③ 同旁内角互补,两条直线平行.
题型一、线与角的有关概念
1.(2022 连云港)已知∠A的补角为60°,则∠A= .
2.(2022·北京)如图,利用工具测量角,则的大小为( )
A.30° B.60° C.120° D.150°
【答案】A
【分析】利用对顶角相等求解.
【详解】解:量角器测量的度数为30°,
由对顶角相等可得,.故选A.
3.(2022·广西贺州)如图,在Rt△ABC中,∠C=90°,∠B=56°,则∠A的度数为( )
A. B. C. D.
【答案】A
【分析】根据直角三角形的两个锐角互余,即可得出∠A的度数.
【详解】解:∵Rt△ABC中,∠C=90°,∠B=56°,
∴∠A=90°-∠B=90°-56°=34°;
故选:A.
4.(2022·河南)如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )
A.26° B.36° C.44° D.54°
【答案】B
【分析】根据垂直的定义可得,根据平角的定义即可求解.
【详解】解: EO⊥CD,,
,.故选:B .
5.(2022·广西)如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么∠BAC的大小为______
【答案】135°##135度
【分析】根据三角板及其摆放位置可得,求解即可.
【详解】,
,
故答案为:135°.
6.(2022·江苏苏州·中考真题)如图,直线AB与CD相交于点O,,,则的度数是( )
A.25° B.30° C.40° D.50°
【答案】D
【分析】根据对顶角相等可得,之后根据,即可求出.
【详解】解:由题可知,
,
.
故选:D.
题型二、相交线与平行线
1.(2022 广东)如图,直线a∥b,∠1=40°,则∠2=( )
A.30° B.40°
C.50° D.60°
2.(2022·甘肃兰州)如图,直线,直线c与直线a,b分别相交于点A,B,,垂足为C.若,则( )
A.52° B.45° C.38° D.26°
【答案】C
【解析】
【分析】
根据平行线的性质可得∠ABC=52°,根据垂直定义可得∠ACB=90°,然后利用直角三角形的两个锐角互余,进行计算即可解答.
【详解】
解:∵ab,
∴∠1=∠ABC=52°,
∵AC⊥b,
∴∠ACB=90°,
∴∠2=90°-∠ABC=38°,
故选:C.
3.(2022·湖南郴州)如图,直线,且直线a,b被直线c,d所截,则下列条件不能判定直线的是( )
A. B. C. D.
【答案】C
【分析】利用平行线的判定条件进行分析即可得出结果.
【详解】解:A、当时,;故A不符合题意;
B、当时,;故B不符合题意;
C、当时,;故C符合题意;
D、∵,则,∵,则,∴;故D不符合题意;故选:C
4.(2022·内蒙古通辽)如图,一束光线先后经平面镜,反射后,反射光线与平行,当时,的度数为( )
A. B. C. D.
【答案】A
【分析】根据题意得:∠ABM=∠OBC, ∠BCO=∠DCN,然后平行线的性质可得∠BCD =70°,即可求解.
【详解】解:根据题意得:∠ABM=∠OBC, ∠BCO=∠DCN,
∵∠ABM=35°,∴∠OBC=35°,∴∠ABC=180°-∠ABM-∠OBC=180°-35°-35°=110°,
∵CD∥AB,∴∠ABC+∠BCD=180°,∴∠BCD=180°-∠ABC=70°,
∵∠BCO+∠BCD+∠DCN=180°, ∠BCO=∠DCN,
∴.故选:A
5.(2022·浙江绍兴·中考真题)如图,把一块三角板的直角顶点B放在直线上,,ACEF,则( )
A.30° B.45° C.60° D.75°
【答案】C
【分析】根据三角板的角度,可得,根据平行线的性质即可求解.
【详解】解:,
ACEF,故选C
6.(2022·湖北鄂州)如图,直线l1l2,点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )
A.10° B.15° C.20° D.30°
【答案】B
【分析】由作图得为等腰三角形,可求出,由l1l2得,从而可得结论.
【详解】解:由作图得,,∴为等腰三角形,∴
∵∠BCA=150°,∴
∵l1l2∴故选B
7.(2022·浙江杭州·中考真题)如图,已知,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10° B.20° C.30° D.40°
【答案】C
【分析】根据三角形外角的性质、平行线的性质进行求解即可;
【详解】解:∵∠C+∠D=∠AEC,∴∠D=∠AEC-∠C=50°-20°=30°,
∵,∴∠A=∠D=30°,故选:C.
8.(2022·海南)如图,直线,是等边三角形,顶点B在直线n上,直线m交于点E,交于点F,若,则的度数是( )
A. B. C. D.
【答案】B
【分析】根据等边三角形的性质可得∠A=60°,再由三角形外角的性质可得∠AEF=∠1-∠A=80°,从而得到∠BEF=100°,然后根据平行线的性质,即可求解.
【详解】解:∵是等边三角形,
∴∠A=60°,
∵∠1=140°,
∴∠AEF=∠1-∠A=80°,
∴∠BEF=180°-∠AEF=100°,
∵,∴∠2=∠BEF=100°.故选:B
9.(2022·黑龙江齐齐哈尔)如图所示,直线a∥b,点A在直线a上,点B在直线b上,AC=BC,∠C=120°,∠1=43°,则∠2的度数为( )
A.57° B.63° C.67° D.73°
【答案】D
【分析】根据等腰三角形的性质可求出,可得出,再根据平行线的性质可得结论.
【详解】解:∵AC=BC,∴是等腰三角形,
∵ ∴
∴
∵a∥b,∴ 故选:D
10.(2022·湖北恩施)已知直线,将含30°角的直角三角板按图所示摆放.若,则( )
A.120° B.130° C.140° D.150°
【答案】D
【分析】根据平行线的性质可得∠3=∠1=120°,再由对顶角相等可得∠4=∠3=120°,然后根据三角形外角的性质,即可求解.
【详解】解:如图,
根据题意得:∠5=30°,
∵,∴∠3=∠1=120°,∴∠4=∠3=120°,
∵∠2=∠4+∠5,∴∠2=120°+30°=150°.故选:D
题型三、角平分线
1.(2021·湖南益阳)如图,与相交于点O,是的平分线,且恰好平分,则_______度.
【答案】60
【解析】
【分析】
先根据角平分线的定义、平角的定义可得,再根据对顶角相等即可得.
【详解】
解:设,
是的平分线,
,
平分,
,
又,
,
解得,即,
由对顶角相等得:,
故答案为:60.
2.(2022·湖南株洲·中考真题)如图所示,点在一块直角三角板上(其中),于点,于点,若,则_________度.
【答案】15
【分析】根据,,判断OB是的角平分线,即可求解.
【详解】解:由题意,,,,
即点O到BC、AB的距离相等,
∴ OB是的角平分线,
∵ ,
∴.故答案为:15.
3.(2022·湖南郴州)如图.在中,,.以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于长为半径作弧,在内两弧相交于点P;作射线AP交BC于点F,过点F作,垂足用G.若,则的周长等于________cm.
【答案】8
【分析】由角平分线的性质,得到,然后求出的周长即可.
【详解】解:根据题意,
在中,,,
由角平分线的性质,得,
∴的周长为:
;
故答案为:8
题型四、线段的垂直平分线
1.(2022·湖北宜昌·中考真题)如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点,.作直线,交于点,交于点,连接.若,,,则的周长为( )
A.25 B.22 C.19 D.18
【答案】C
【分析】由垂直平分线的性质可得BD=CD,由△ABD的周长=AB+AD+BD=AB+AD+CD=AB+AC得到答案.
【详解】解:由作图的过程可知,DE是BC的垂直平分线,∴BD=CD,
∵,,∴ △ABD的周长=AB+AD+BD=AB+AD+CD=AB+AC=19.故选:C
2.(2022·四川成都)如图,在中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交边于点.若,,,则的长为_________.
【答案】7
【分析】连接EC,依据垂直平分线的性质得.由已知易得,在Rt△AEC中运用勾股定理求得AE,即可求得答案.
【详解】解:由已知作图方法可得,是线段的垂直平分线,
连接EC,如图,
所以,
所以,
所以∠BEC=∠CEA=90°,
因为,,
所以,
在中,,
所以,
因此的长为7.
故答案为:7.
3.(2022·四川达州·中考真题)如图,在中,,,分别以点A,B为圆心,大于的长为半径作弧,两弧分别相交于点M,N,作直线,交于点D,连接,则的度数为_____.
【答案】##50度
【分析】根据作图可知,,根据直角三角形两个锐角互余,可得,根据即可求解.
【详解】解:∵在中,,,
∴,
由作图可知是的垂直平分线,
,
,
,
故答案为:.
模块四 三角形
专题1 线与角
线与角 线 直线 经过两点有且只有一条直线.直线是向两方无限延伸的,直线没有端点.
射线 直线上一点和它一旁的部分叫做射线,这点叫做射线的端点,射线向一方无限延伸,射线只有一个端点.
线段 1、直线上两个点和它们之间的部分叫做线段.线段有两个端点,有长短之分,将某一线段分成两条相等的线段的点叫做该线段的中点. 2、两点确定一条直线,两点之间线段最短,两点之间线段的长度叫做两点之间的距离.
角 角度换算 1°=60',1'=60″. 1周角=2平角=4直角=360°.
余角 如果两个角的和等于90°,就说这两个角互为余角; 同角或等角的余角相等.
补角 如果两个角的和等于180°,就说这两个角互为补角; 同角或等角补角相等.
对顶角 一个角的两边是另一个角的两边的反向延长线,则称这两个角是对顶角,对顶角相等.
角平分线 性质 角平分线上的点到角两边的距离相等
判定 到角两边距离相等的点在角平分线上.
线段垂直平分线 定义 垂直平分一条线段的直线叫做线段的垂直平分线.
性质 线段的垂直平分线上的点到这条线段两个端点的距离相等,
判定 到线段两端距离相等的点在线段的垂直平分线上.
垂线 在同一平面内,过一点有且只有一条直线与已知直线垂直. 垂线段公理:直线外一点与已知线段连接的所有线段中,垂线段最短.
平行线 过直线外一点,有且只有一条直线与这条直线平行.
性质 ① 两条直线平行,同位角相等; ② 两条直线平行,内错角相等; ③ 两条直线平行,同旁内角互补.
判定 ① 同位角相等,两条直线平行; ② 内错角相等,两条直线平行; ③ 同旁内角互补,两条直线平行.
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
题型一、线与角的有关概念
1.(2022 连云港)已知∠A的补角为60°,则∠A= .
2.(2022·北京)如图,利用工具测量角,则的大小为( )
A.30° B.60° C.120° D.150°
3.(2022·广西贺州)如图,在Rt△ABC中,∠C=90°,∠B=56°,则∠A的度数为( )
A. B. C. D.
4.(2022·河南)如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )
A.26° B.36° C.44° D.54°
5.(2022·广西)如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么∠BAC的大小为______
6.(2022·江苏苏州·中考真题)如图,直线AB与CD相交于点O,,,则的度数是( )
A.25° B.30° C.40° D.50°
题型二、相交线与平行线
1.(2022 广东)如图,直线a∥b,∠1=40°,则∠2=( )
A.30° B.40°
C.50° D.60°
2.(2022·甘肃兰州)如图,直线,直线c与直线a,b分别相交于点A,B,,垂足为C.若,则( )
A.52° B.45° C.38° D.26°
3.(2022·湖南郴州)如图,直线,且直线a,b被直线c,d所截,则下列条件不能判定直线的是( )
A. B. C. D.
4.(2022·内蒙古通辽)如图,一束光线先后经平面镜,反射后,反射光线与平行,当时,的度数为( )
A. B. C. D.
5.(2022·浙江绍兴·中考真题)如图,把一块三角板的直角顶点B放在直线上,,ACEF,则( )
A.30° B.45° C.60° D.75°
6.(2022·湖北鄂州)如图,直线l1l2,点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )
A.10° B.15° C.20° D.30°
7.(2022·浙江杭州·中考真题)如图,已知,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10° B.20° C.30° D.40°
8.(2022·海南)如图,直线,是等边三角形,顶点B在直线n上,直线m交于点E,交于点F,若,则的度数是( )
A. B. C. D.
9.(2022·黑龙江齐齐哈尔)如图所示,直线a∥b,点A在直线a上,点B在直线b上,AC=BC,∠C=120°,∠1=43°,则∠2的度数为( )
A.57° B.63° C.67° D.73°
10.(2022·湖北恩施)已知直线,将含30°角的直角三角板按图所示摆放.若,则( )
A.120° B.130° C.140° D.150°
题型三、角平分线
1.(2021·湖南益阳)如图,与相交于点O,是的平分线,且恰好平分,则_______度.
2.(2022·湖南株洲·中考真题)如图所示,点在一块直角三角板上(其中),于点,于点,若,则_________度.
3.(2022·湖南郴州)如图.在中,,.以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于长为半径作弧,在内两弧相交于点P;作射线AP交BC于点F,过点F作,垂足用G.若,则的周长等于________cm.
题型四、线段的垂直平分线
1.(2022·湖北宜昌·中考真题)如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点,.作直线,交于点,交于点,连接.若,,,则的周长为( )
A.25 B.22 C.19 D.18
2.(2022·四川成都)如图,在中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交边于点.若,,,则的长为_________.
3.(2022·四川达州·中考真题)如图,在中,,,分别以点A,B为圆心,大于的长为半径作弧,两弧分别相交于点M,N,作直线,交于点D,连接,则的度数为_____.
2023年中考数学第一轮复习
模块四 三角形
专题1 线与角
线与角 线 直线 经过两点有且只有一条直线.直线是向两方无限延伸的,直线没有端点.
射线 直线上一点和它一旁的部分叫做射线,这点叫做射线的端点,射线向一方无限延伸,射线只有一个端点.
线段 1、直线上两个点和它们之间的部分叫做线段.线段有两个端点,有长短之分,将某一线段分成两条相等的线段的点叫做该线段的中点. 2、两点确定一条直线,两点之间线段最短,两点之间线段的长度叫做两点之间的距离.
角 角度换算 1°=60',1'=60″. 1周角=2平角=4直角=360°.
余角 如果两个角的和等于90°,就说这两个角互为余角; 同角或等角的余角相等.
补角 如果两个角的和等于180°,就说这两个角互为补角; 同角或等角补角相等.
对顶角 一个角的两边是另一个角的两边的反向延长线,则称这两个角是对顶角,对顶角相等.
角平分线 性质 角平分线上的点到角两边的距离相等
判定 到角两边距离相等的点在角平分线上.
线段垂直平分线 定义 垂直平分一条线段的直线叫做线段的垂直平分线.
性质 线段的垂直平分线上的点到这条线段两个端点的距离相等,
判定 到线段两端距离相等的点在线段的垂直平分线上.
垂线 在同一平面内,过一点有且只有一条直线与已知直线垂直. 垂线段公理:直线外一点与已知线段连接的所有线段中,垂线段最短.
平行线 过直线外一点,有且只有一条直线与这条直线平行.
性质 ① 两条直线平行,同位角相等; ② 两条直线平行,内错角相等; ③ 两条直线平行,同旁内角互补.
判定 ① 同位角相等,两条直线平行; ② 内错角相等,两条直线平行; ③ 同旁内角互补,两条直线平行.
题型一、线与角的有关概念
1.(2022 连云港)已知∠A的补角为60°,则∠A= .
2.(2022·北京)如图,利用工具测量角,则的大小为( )
A.30° B.60° C.120° D.150°
【答案】A
【分析】利用对顶角相等求解.
【详解】解:量角器测量的度数为30°,
由对顶角相等可得,.故选A.
3.(2022·广西贺州)如图,在Rt△ABC中,∠C=90°,∠B=56°,则∠A的度数为( )
A. B. C. D.
【答案】A
【分析】根据直角三角形的两个锐角互余,即可得出∠A的度数.
【详解】解:∵Rt△ABC中,∠C=90°,∠B=56°,
∴∠A=90°-∠B=90°-56°=34°;
故选:A.
4.(2022·河南)如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )
A.26° B.36° C.44° D.54°
【答案】B
【分析】根据垂直的定义可得,根据平角的定义即可求解.
【详解】解: EO⊥CD,,
,.故选:B .
5.(2022·广西)如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么∠BAC的大小为______
【答案】135°##135度
【分析】根据三角板及其摆放位置可得,求解即可.
【详解】,
,
故答案为:135°.
6.(2022·江苏苏州·中考真题)如图,直线AB与CD相交于点O,,,则的度数是( )
A.25° B.30° C.40° D.50°
【答案】D
【分析】根据对顶角相等可得,之后根据,即可求出.
【详解】解:由题可知,
,
.
故选:D.
题型二、相交线与平行线
1.(2022 广东)如图,直线a∥b,∠1=40°,则∠2=( )
A.30° B.40°
C.50° D.60°
2.(2022·甘肃兰州)如图,直线,直线c与直线a,b分别相交于点A,B,,垂足为C.若,则( )
A.52° B.45° C.38° D.26°
【答案】C
【解析】
【分析】
根据平行线的性质可得∠ABC=52°,根据垂直定义可得∠ACB=90°,然后利用直角三角形的两个锐角互余,进行计算即可解答.
【详解】
解:∵ab,
∴∠1=∠ABC=52°,
∵AC⊥b,
∴∠ACB=90°,
∴∠2=90°-∠ABC=38°,
故选:C.
3.(2022·湖南郴州)如图,直线,且直线a,b被直线c,d所截,则下列条件不能判定直线的是( )
A. B. C. D.
【答案】C
【分析】利用平行线的判定条件进行分析即可得出结果.
【详解】解:A、当时,;故A不符合题意;
B、当时,;故B不符合题意;
C、当时,;故C符合题意;
D、∵,则,∵,则,∴;故D不符合题意;故选:C
4.(2022·内蒙古通辽)如图,一束光线先后经平面镜,反射后,反射光线与平行,当时,的度数为( )
A. B. C. D.
【答案】A
【分析】根据题意得:∠ABM=∠OBC, ∠BCO=∠DCN,然后平行线的性质可得∠BCD =70°,即可求解.
【详解】解:根据题意得:∠ABM=∠OBC, ∠BCO=∠DCN,
∵∠ABM=35°,∴∠OBC=35°,∴∠ABC=180°-∠ABM-∠OBC=180°-35°-35°=110°,
∵CD∥AB,∴∠ABC+∠BCD=180°,∴∠BCD=180°-∠ABC=70°,
∵∠BCO+∠BCD+∠DCN=180°, ∠BCO=∠DCN,
∴.故选:A
5.(2022·浙江绍兴·中考真题)如图,把一块三角板的直角顶点B放在直线上,,ACEF,则( )
A.30° B.45° C.60° D.75°
【答案】C
【分析】根据三角板的角度,可得,根据平行线的性质即可求解.
【详解】解:,
ACEF,故选C
6.(2022·湖北鄂州)如图,直线l1l2,点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )
A.10° B.15° C.20° D.30°
【答案】B
【分析】由作图得为等腰三角形,可求出,由l1l2得,从而可得结论.
【详解】解:由作图得,,∴为等腰三角形,∴
∵∠BCA=150°,∴
∵l1l2∴故选B
7.(2022·浙江杭州·中考真题)如图,已知,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10° B.20° C.30° D.40°
【答案】C
【分析】根据三角形外角的性质、平行线的性质进行求解即可;
【详解】解:∵∠C+∠D=∠AEC,∴∠D=∠AEC-∠C=50°-20°=30°,
∵,∴∠A=∠D=30°,故选:C.
8.(2022·海南)如图,直线,是等边三角形,顶点B在直线n上,直线m交于点E,交于点F,若,则的度数是( )
A. B. C. D.
【答案】B
【分析】根据等边三角形的性质可得∠A=60°,再由三角形外角的性质可得∠AEF=∠1-∠A=80°,从而得到∠BEF=100°,然后根据平行线的性质,即可求解.
【详解】解:∵是等边三角形,
∴∠A=60°,
∵∠1=140°,
∴∠AEF=∠1-∠A=80°,
∴∠BEF=180°-∠AEF=100°,
∵,∴∠2=∠BEF=100°.故选:B
9.(2022·黑龙江齐齐哈尔)如图所示,直线a∥b,点A在直线a上,点B在直线b上,AC=BC,∠C=120°,∠1=43°,则∠2的度数为( )
A.57° B.63° C.67° D.73°
【答案】D
【分析】根据等腰三角形的性质可求出,可得出,再根据平行线的性质可得结论.
【详解】解:∵AC=BC,∴是等腰三角形,
∵ ∴
∴
∵a∥b,∴ 故选:D
10.(2022·湖北恩施)已知直线,将含30°角的直角三角板按图所示摆放.若,则( )
A.120° B.130° C.140° D.150°
【答案】D
【分析】根据平行线的性质可得∠3=∠1=120°,再由对顶角相等可得∠4=∠3=120°,然后根据三角形外角的性质,即可求解.
【详解】解:如图,
根据题意得:∠5=30°,
∵,∴∠3=∠1=120°,∴∠4=∠3=120°,
∵∠2=∠4+∠5,∴∠2=120°+30°=150°.故选:D
题型三、角平分线
1.(2021·湖南益阳)如图,与相交于点O,是的平分线,且恰好平分,则_______度.
【答案】60
【解析】
【分析】
先根据角平分线的定义、平角的定义可得,再根据对顶角相等即可得.
【详解】
解:设,
是的平分线,
,
平分,
,
又,
,
解得,即,
由对顶角相等得:,
故答案为:60.
2.(2022·湖南株洲·中考真题)如图所示,点在一块直角三角板上(其中),于点,于点,若,则_________度.
【答案】15
【分析】根据,,判断OB是的角平分线,即可求解.
【详解】解:由题意,,,,
即点O到BC、AB的距离相等,
∴ OB是的角平分线,
∵ ,
∴.故答案为:15.
3.(2022·湖南郴州)如图.在中,,.以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于长为半径作弧,在内两弧相交于点P;作射线AP交BC于点F,过点F作,垂足用G.若,则的周长等于________cm.
【答案】8
【分析】由角平分线的性质,得到,然后求出的周长即可.
【详解】解:根据题意,
在中,,,
由角平分线的性质,得,
∴的周长为:
;
故答案为:8
题型四、线段的垂直平分线
1.(2022·湖北宜昌·中考真题)如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点,.作直线,交于点,交于点,连接.若,,,则的周长为( )
A.25 B.22 C.19 D.18
【答案】C
【分析】由垂直平分线的性质可得BD=CD,由△ABD的周长=AB+AD+BD=AB+AD+CD=AB+AC得到答案.
【详解】解:由作图的过程可知,DE是BC的垂直平分线,∴BD=CD,
∵,,∴ △ABD的周长=AB+AD+BD=AB+AD+CD=AB+AC=19.故选:C
2.(2022·四川成都)如图,在中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交边于点.若,,,则的长为_________.
【答案】7
【分析】连接EC,依据垂直平分线的性质得.由已知易得,在Rt△AEC中运用勾股定理求得AE,即可求得答案.
【详解】解:由已知作图方法可得,是线段的垂直平分线,
连接EC,如图,
所以,
所以,
所以∠BEC=∠CEA=90°,
因为,,
所以,
在中,,
所以,
因此的长为7.
故答案为:7.
3.(2022·四川达州·中考真题)如图,在中,,,分别以点A,B为圆心,大于的长为半径作弧,两弧分别相交于点M,N,作直线,交于点D,连接,则的度数为_____.
【答案】##50度
【分析】根据作图可知,,根据直角三角形两个锐角互余,可得,根据即可求解.
【详解】解:∵在中,,,
∴,
由作图可知是的垂直平分线,
,
,
,
故答案为:.
同课章节目录
