第七章 随机变量及其分布--高二年级数学人教版(2019)选择性必修三单元练习(含解析)
文档属性
| 名称 | 第七章 随机变量及其分布--高二年级数学人教版(2019)选择性必修三单元练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 198.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 16:49:36 | ||
图片预览




文档简介
随机变量及其分布
1. 设随机变量∽,∽,若,则的值为( )
A. B. C. D.
2. 某单位为了响应疫情期间有序复工复产的号召,组织从疫区回来的甲、乙、丙、丁4名员工进行核酸检测,现采用抽签法决定检测顺序,在“员工甲不是第一个检测,员工乙不是最后一个检测”的条件下,员工丙第一个检测的概率为( )
A. B. C. D.
3. 投壶是从先秦延续至清末的汉民族传统礼仪和宴饮游戏,在春秋战国时期较为盛行.如图为一幅唐朝的投壶图,假设甲、乙是唐朝的两位投壶游戏参与者,且甲、乙每次投壶投中的概率分别为,每人每次投壶相互独立.若约定甲投壶2次,乙投壶3次,投中次数多者胜,则甲最后获胜的概率为( )
A. B. C. D.
4. 根据国家关于加强禁毒教育要求,龙港中学举办了“禁毒知识竞赛”,采用抽题问答形式.设抽题盒中a道简单题,b道中等题,c道难题,且规定:抽中简单题并回答正确得1分,抽中中等题并回答正确得2分,抽中难题并回答正确得3分.现在从盒子中取出1道题并回答正确,记所得分为若,,则a:b:( )
A. 4:1:1 B. 5:2:1 C. 6:3:1 D. 6:3:2
5. 某卡车为乡村小学运送书籍,共装有10个纸箱,其中5箱英语书、2箱数学书、3箱语文书.到目的地时发现丢失一箱,但不知丢失哪一箱.现从剩下9箱中任意打开两箱,结果都是英语书,则丢失的一箱也是英语书的概率为( )
A. B. C. D.
6. 已知数列满足,且对任意,等概率地取或,设的值为随机变量,则( )
A. B.
C. D.
7. 托马斯贝叶斯在研究“逆向概率”的问题中得到了一个公式:,这个公式被称为贝叶斯公式贝叶斯定理,其中称为B的全概率.假设甲袋中有3个白球和3个红球,乙袋中有2个白球和2个红球.现从甲袋中任取2个球放入乙袋,再从乙袋中任取2个球.已知从乙袋中取出的是2个红球,则从甲袋中取出的也是2个红球的概率为( )
A. B. C. D.
8. 有甲、乙两个盒子,甲盒子里有1个红球,乙盒子里有3个红球和3个黑球,现从乙盒子里随机取出个球放入甲盒子后,再从甲盒子里随机取一球,记取到的红球个数为个,则随着的增加,下列说法正确的是( )
A. 增加,增加 B. 增加,减小
C. 减小,增加 D. 减小,减小
9. 已知,则( )
A. B. C. D.
10. 已知某校高三年级有1000人参加一次数学模拟考试,现把这次考试的分数转换为标准分,标准分的分数转换区间为,若使标准分X服从正态分布,参考数据:;;则
A. 这次考试标准分超过180分的约有450人
B. 这次考试标准分在内的人数约为997
C. 甲、乙、丙三人恰有2人的标准分超过180分的概率为
D.
11. 某市组织2022年度高中校园足球比赛,共有10支球队报名参赛.比赛开始前将这10支球队分成两个小组,每小组5支球队,其中获得2021年度冠、亚军的两支球队分别在第一小组和第二小组,剩余8支球队抽签分组.已知这8支球队中包含甲、乙两队,记“甲队分在第一小组”为事件,“乙队分在第一小组”为事件,“甲、乙两队分在同一小组”为事件,则( )
A. B.
C. D. 事件与事件相互独立
12. 一个袋子中装有除颜色外完全相同的10个球,其中有6个黑球,4个白球,现从中任取4个球,记随机变量X为取出白球的个数,随机变量Y为取出黑球的个数,若取出一个白球得2分,取出一个黑球得1分,随机变量Z为取出4个球的总得分,则下列结论中正确的是( )
A. B. C. D.
13. 勤洗手、常通风、戴口罩是切断新冠肺炎传播的有效手段.经调查疫情期间某小区居民人人养成了出门戴口罩的好习惯,且选择佩戴一次性医用口罩的概率为 p,每人是否选择佩戴一次性医用口罩是相互独立的.现随机抽取5 位该小区居民,其中选择佩戴一次性医用口罩的人数为 X,且,,则p的值为__________.
14. 抽样表明,某地区新生儿体重X近似服从正态分布假设随机抽取r个新生儿体检,记表示抽取的r个新生儿体重在以外的个数.若的数学期望,则r的最大值是__________.
注:若随机变量X∽,则
15. 一猎人带着一把猎枪到山里去打猎,猎枪每次可以装3发子弹,当他遇见一只野兔时,开第一枪命中野免的概率为,若第一枪没有命中,猎人开第二枪,命中野免的概率为,若第二枪也没有命中,猎人开第三枪,命中野兔的概率为,若3发子弹都没打中,野兔就逃跑了,则已知野兔被击中的条件下,是猎人开第二枪命中的概率为__________
16. 甲袋中有3个红球,2个白球和1个黑球,乙袋中有4个红球,1 个白球和1个黑球除颜色外,球的大小、形状完全相同先从甲袋中随机取出1球放入乙袋,再从乙袋中随机取出1球.分别以,,表示由甲袋取出的球是红球,白球和黑球的事件,以B表示由乙袋取出的球是红球的事件,则__________,__________.
17. 第24届冬季奥林匹克运动会于2022年2月在北京市和张家口市联合举行.甲、乙是单板滑雪坡面障碍技巧项目的参赛选手,二人在练习赛中均需要挑战3次某高难度动作,每次挑战的结果只有成功和失败两种.
甲在每次挑战中,成功的概率都为设X为甲在3次挑战中成功的次数,求X的分布列和数学期望;
乙在第一次挑战时,成功的概率为,受心理因素影响,从第二次开始,每次成功的概率会发生改变,其规律为:若前一次成功,则该次成功的概率比前一次成功的概率增加若前一次失败,则该次成功的概率比前一次成功的概率减少求乙在3次挑战中有且只有2次成功的条件下,第三次成功的概率.
18. 某单位有A,B两个餐厅为员工提供午餐与晚餐服务,甲、乙两位员工每个工作日午餐和晚餐都在单位就餐,近100个工作日选择餐厅就餐情况统计如下:
选择餐厅情况午餐,晚餐
甲员工 30天 20天 40天 10天
乙员工 20天 25天 15天 40天
假设甲、乙员工选择餐厅相互独立,用频率估计概率.
分别估计一天中甲员工午餐和晚餐都选择A餐厅就餐的概率,乙员工午餐和晚餐都选择B餐厅就餐的概率;
记X为甲、乙两员工在一天中就餐餐厅的个数,求X的分布列和数学期望;
试判断甲、乙员工在晚餐选择B餐厅就餐的条件下,哪位员工更有可能午餐选择A餐厅就餐,并说明理由.
19. 现有一种射击训练,每次训练都是由高射炮向目标飞行物连续发射三发炮弹,每发炮弹击中目标飞行物与否相互独立.已知射击训练有A,B两种型号的炮弹,对于A型号炮弹,每发炮弹击中目标飞行物的概率均为,且击中一弹目标飞行物坠毁的概率为,击中两弹目标飞行物必坠毁;对于B型号炮弹,每发炮弹击中目标飞行物的概率均为,且击中一弹目标飞行物坠毁的概率为,击中两弹目标飞行物坠毁的概率为,击中三弹目标飞行物必坠毁.
在一次训练中,使用B型号炮弹,求q满足什么条件时,才能使得至少有一发炮弹命中目标飞行物的概率不低于
若,试判断在一次训练中选用A型号炮弹还是B型号炮弹使得目标飞行物坠毁的概率更大 并说明理由.
20. 现有A,B两个项目,投资A项目100万元,一年后获得的利润为万元,根据市场分析,的概率分布列为
12
P
投资B项目100万元,一年后获得的利润万元与B项目产品价格的调整价格上调或下调有关已知产品价格在一年内进行2次独立的调整,且在每次调整中价格下调的概率都是经专家测算评估,B项目产品价格的下调次数与一年后获得相应利润的关系如下表所示:
B项目产品价格一年内下调的次数X 0 1 2
投资100万元一年后获得的利润万元 13 2
求的方差
求的分布列
若,根据投资获得利润的差异,你愿意选择投资哪个项目参考数据:
21. 为了深入贯彻党的十九大和十九届五中全会精神,坚持以新时代中国特色社会主义思想为指导,落实立德树人根本任务,着眼建设高质量教育体系,强化学校教育主阵地作用,深化校外培训机构治理,构建教育良好生态,有效缓解家长焦虑情绪,促进学生全面发展、健康成长.教育部门最近出台了“双减”政策,即有效减轻义务教育阶段学生过重作业负担和校外培训负担,持续规范校外培训包括线上培训和线下培训“双减”政策的出台对校外的培训机构经济效益产生了严重影响.某大型校外培训机构为了规避风险,寻求发展制定科学方案,工作人员对2020年的前200名报名学员消费等情况进行了统计整理,其中消费情况数据如表.
消费金额千元
人数 30 50 60 20 30 10
该大型校外培训机构转型方案之一是将文化科主阵地辅导培训向音体美等兴趣爱好培训转移,为了深入了解当前学生的兴趣爱好,工作人员利用分层抽样的方法在消费金额为和的学员中抽取了5人,再从这5人中选取3人进行有奖问卷调查,求抽取的3人中消费金额为的人数的分布列和数学期望;
以频率估计概率,假设该大型校外培训机构2020年所有学员的消费可视为服从正态分布,,分别为报名前200名学员消费的平均数以及方差同一区间的花费用区间的中点值替代
试估计该机构学员2020年消费金额为的概率保留一位小数;
若从该机构2020年所有学员中随机抽取4人,记消费金额为的人数为,求的分布列及方差.
参考数据:;若随机变量服从正态分布,则,,
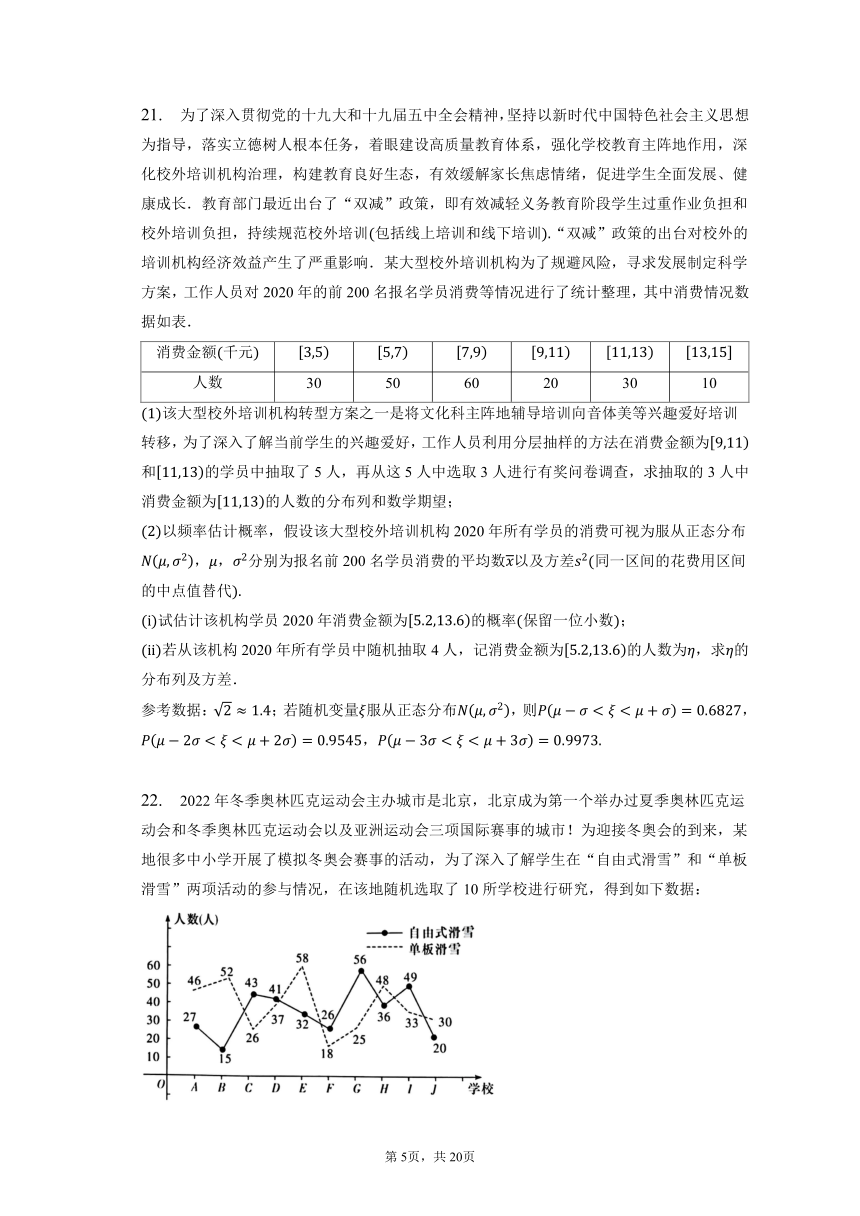
22. 2022年冬季奥林匹克运动会主办城市是北京,北京成为第一个举办过夏季奥林匹克运动会和冬季奥林匹克运动会以及亚洲运动会三项国际赛事的城市!为迎接冬奥会的到来,某地很多中小学开展了模拟冬奥会赛事的活动,为了深入了解学生在“自由式滑雪”和“单板滑雪”两项活动的参与情况,在该地随机选取了10所学校进行研究,得到如下数据:
在这10所学校中随机选取3所来调查研究,求这3所学校参与“自由式滑雪”都超过40人的概率;
“单板滑雪”参与人数超过45人的学校可以作为“基地学校”,现在从这10所学校中随机选出3所,记X为选出可作“基地学校”的学校个数,求X的分布列和数学期望;
现在有一个“单板滑雪”集训营,对“滑行、转弯、停止”这3个动作技巧进行集训,且在集训中进行了多轮测试.规定:在一轮测试中,这3个动作中至少有2个动作达到“优秀”,则该轮测试记为“优秀”.在集训测试中,小明同学3个动作中每个动作达到“优秀”的概率均为,每个动作互不影响且每轮测试互不影响.如果小明同学在集训测试中要想获得“优秀”的次数的平均值达到5次,那么理论上至少要进行多少轮测试?
答案和解析
1.【答案】B
【解析】
【分析】
本题考查二项分布的概率计算,属于中档题.
首先根据求出p的值,再计算的值.
【解答】
解:因为随机变量,
所以,
解得,所以,
则
故选
2.【答案】B
【解析】
【分析】
本题考查应用概率解决实际问题,是基础题.
设员工甲不是第一个检测,员工乙不是最后一个检测为事件A,员工丙第一个检测为事件B,再对事件A发生的情况下发生事件B的概率进行分析,即可求解.
【解答】
解:设事件员工甲不是第一个检测,员工乙不是最后一个检测,事件员工丙第一个检测,
所以,
所以
故答案为
3.【答案】B
【解析】
【分析】
本题考查相互独立事件同时发生的概率,属于中档题.
由题可得甲最后获胜的情况有3种,分别求解概率再相加即得.
【解答】
解:由题意可得,甲、乙每次投壶投中的概率分别为,若约定甲投壶2次,乙投壶3次,投中次数多者胜,则甲最后获胜的情况有3种:
①甲投中1次,乙投中0次,则概率为
;
②甲投中2次,乙投中1次,则概率为
;
③甲投中2次,乙投中0次,则概率为
;
所以甲最后获胜的概率为
故选
4.【答案】B
【解析】
【分析】
由题意可得,所有可能的取值为1,2,3,分别求出对应的概率,再结合期望和方差的公式,即可求解.
本题主要考查期望与方差的公式,考查转化能力,属于中档题.
【解答】
解:由题意可得,所有可能的取值为1,2,3,
则,,,
,
,
所以,,即,,
故a:b::2:
故选:
5.【答案】B
【解析】
【分析】
本题考查贝叶斯公式的应用,考查全概率公式的应用,属于中档题.
A表示丢失一箱后任取两箱是英语书,用表示丢失的一箱为k,,2,3分别表示英语书、数学书、语文书.根据全概率公式求得,根据贝叶斯公式可得,进而得解.
【解答】
解:用A表示丢失一箱后任取两箱是英语书,用表示丢失的一箱为k,,2,3分别表示英语书、数学书、语文书.
由全概率公式得
故选
6.【答案】D
【解析】
【分析】
本题考查概率的求法,考查离散型随机变量的分布列、数学期望的求法,考查相互独立事件概率乘法公式等基础知识,考查运算求解能力,是中档题.
根据题意,分别分析出当n分别取2,3,4,5时所对应的值,以及每个的对应的概率,即可判断出正确选项.
【解答】
解:依题意或,且,
的可能取值为,,,,
,
,,
,
,
由此排除A和B;
的可能取值为,,,,,,
,
,
,
的可能取值为4,2,0,,
,
,
所以,排除
因为,,所以,
故选:
7.【答案】C
【解析】
【分析】
本题考查了条件概率,贝叶斯公式及古典概型,属于中档题.
根据题意,先分析求解设从甲袋中取出2个球,其中红球的个数为i个的事件为,事件的概率为,从乙袋中取出2个球,其中红球的个数为2个的事件为B,事件B的概率为,再分别分析三种情况求解即可.
【解答】
解:设从甲袋中取出2个球,其中红球的个数为i个的事件为,事件的概率为,从乙袋中取出2个球,其中红球的个数为2个的事件为B,事件B的概率为,由题意:
①,;
②,;
③,;
根据贝叶斯公式可得,从乙袋中取出的是2个红球,则从甲袋中取出的也是2个红球的概率为
故选:C
8.【答案】C
【解析】
【分析】
本题考查了超几何分布、两点分布,分布列与数学期望,考查了推理能力计算能力,属于难题.
依题意,从乙盒子里随机取出n个球,含有红球个数X服从超几何分布,即,故,再从乙盒子里随机取出n个球,含有红球个数X服从超几何分布,即,服从两点分布,所以 ,随着n的增大,减小;, 随着n的增大,增大;
【解答】
解:依题意,从乙盒子里随机取出n个球,含有红球个数X服从超几何分布,即,
其中 ,其中,且,
故从甲盒中取球,相当于从含有 个红球的个球中取一球,取到红球个数为个,
故,随着n的增大,减小;
,随着n的增大,增大;
故选
9.【答案】BCD
【解析】
【分析】
本题主要考查条件概率公式,全概率公式和事件公式,属于中档题;
根据条件概率公式,全概率公式和事件公式可逐一进行判断.
【解答】
解:对于B:, , 故选项CB正确;
对于C:,故选项 C正确;
对于A:由全概率公式得:
, ,
, 故选项A错;
对于D:,故选项 D正确;
故选:
10.【答案】BC
【解析】
【分析】
本题考查正态分布曲线性质及概率计算,属中档题目.
根据题意和正态分布的知识对选项逐一分析计算即可.
【解答】
解:由题意X服从正态分布,
,,故A不正确;
,,故B正确;
甲、乙、丙三人恰有2人的标准分超过180分的概率,故C正确;
因为,
,
所以 ,故D不正确.
故选
11.【答案】ABD
【解析】
【分析】
本题主要考查相互独立事件的概率乘法公式,古典概型,排列组合的应用,属于中档题.
根据已知条件,结合排列组合知识,以及相互独立事件的概率乘法公式,即可依次求解.
【解答】
解:对于A,甲队分在第一小组和第二小组的概率相等,且两种情况有且只有一种情况发生,
,故A正确,
对于B,8支球队抽签分组共有种不同方法,甲、乙两队分在同小组共有种不同方法,
所以甲,乙两队分在同一小组的概率,故B正确,
对于C,,
,故C错误,
对于D,,,
故,
故事件与事件相互独立,故D正确.
故选:
12.【答案】BD
【解析】
【分析】
本题主要考查超几何分布的概率和均值,属于较难题.
【解答】
解:随机变量X的所有可能取值为0,1,2,3,4,且服从超几何分布.
,,A错误.
,,
,
X 0 1 2 3 4
p
因此,
由题知,B正确.
故Y的分布列如下:
Y 0 1 2 3 4
p
因此
,C错误.
,D正确.
13.【答案】
【解析】
【分析】
本题主要考查了二项分布,属于基础题.
由题意,根据二项分布概率计算公式和方差公式计算出p值即可.
【解答】
解:由题意,,
且,
根据二项分布概率公式有,,
解得,
故,
则,
解得或舍去,
故答案为:
14.【答案】16
【解析】
【分析】
本题考查正态分布的概率计算,以及二项分布的期望公式,属于中档题.
根据正态分布的性质求出在之外的概率,从而得到 ,根据二项分布的期望公式得到不等式,解得即可.
【解答】
解:依题意,
所以在之外的概率,
则,
则,
因为,
所以,
解得 ,
因为 ,
所以r的最大值为
故答案为
15.【答案】
【解析】
【分析】
本题考查了互斥事件和条件概率,属于中档题.
利用互斥事件至少有一个发生的概率得“野兔被击中”的概率,再利用条件概率,计算得结论.
【解答】
解:设“猎人第一枪击中野兔”,“猎人第二枪击中野兔”,
“猎人第三枪击中野兔”,“野兔被击中”,
则互斥,且,,,
因此
,
所以
故答案为
16.【答案】
【解析】
【分析】
本题主要考查条件概率公式、全概率公式等基础知识,考查运算求解能力,属于中档题.
先分别求出,,再由,能求出;分别求出,,,,,,从而求出,,,再由,能求出
【解答】
解:甲袋中有3个红球,2个白球和1个黑球,乙袋中有4个红球,1个白球和1个黑球除颜色外,球的大小、形状完全相同
先从甲袋中随机取出1球放入乙袋,再从乙袋中随机取出1球.
分别以,,表示由甲袋取出的球是红球,白球和黑球的事件,以B表示由乙袋取出的球是红球的事件,
则,,
,
,,,
,,,
,,,
故答案为:;
17.【答案】解:由题意得,X∽,则,其中,1,2,3,
则X的分布列为:
X 0 1 2 3
P
则
设“乙在3次挑战中有且只有2次成功”,“乙在3次挑战中第三次成功”,
【解析】本题考查二项分布以及数学期望,考查条件概率的应用,考查了运算能力,属于中档题.
根据题意可得X∽,根据二项分布的概率以及期望公式即可求解;
根据条件概率的求法公式即可求解.
18.【答案】解:设事件C为“一天中甲员工午餐和晚餐都选择A餐厅就餐”,
事件D为“乙员工午餐和晚餐都选择B餐厅就餐”
因为100个工作日中甲员工午餐和晚餐都选择A餐厅就餐的天数为30,
乙员工午餐和晚餐都选择B餐厅就餐的天数为40,
所以,
由题意知,甲员工午餐和晚餐都选择B餐厅就餐的概率为,
乙员工午餐和晚餐都选择A餐厅就餐的概率为,
记X为甲、乙两员工在一天中就餐餐厅的个数,则X的所有可能取值为1、2,
所以,,
所以X的分布列为:
X 1 2
P
所以X的数学期望
设“甲员工晚餐选择B餐厅就餐”,“乙员工晚餐选择B餐厅就餐”,
“甲员工在午餐时选择A餐厅就餐”,“乙员工在午餐时选择A餐厅就餐”,
则,,因为,
所以在已知晚餐选择B 餐厅就餐的条件下,甲员工更有可能在午餐时选择 A餐厅就餐.
【解析】本题考查离散型随机变量的分布列和均值、古典概型及其计算、条件概率的概念与计算,属于中档题.
根据题意结合古典概型的概率公式,即可求出一天中甲员工午餐和晚餐都选择A餐厅就餐的概率,乙员工午餐和晚餐都选择B餐厅就餐的概率;
由题意确定X的所有可能取值为和对应概率,从而得到X的分布列,利用随机变量的期望公式求出;
利用条件概率公式分别求出“甲、乙员工在晚餐选择B餐厅就餐的条件下,午餐选择A餐厅就餐”的概率,比较二者概率大小即可判断哪位员工更有可能午餐选择A餐厅就餐.
19.【答案】解:因为发射B型号炮弹3发至少命中一发的对立事件是一发都未命中,且每发炮弹击中与否相互独立,
所以发射B型号炮弹3发至少命中一发的概率为,
所以,
解得,
所以,
选用B型号炮弹使得目标飞行物坠毁的概率更大,理由如下:
记事件“发射A型号炮弹目标飞行物坠毁”,“发射A型号炮弹命中i发”,
所以
,
同理记“发射B型号炮弹目标飞行物坠毁”,“发射B型号炮弹命中j发”,
所以
,
作差比较得,
记,则恒成立,
所以在上单调递减,
因为,
所以当时,,即,
所以选用B型号炮弹使得目标飞行物坠毁的概率更大.
【解析】本题主要考查相互独立事件的概率乘法公式,对立事件,互斥事件,全概率公式,利用导数求函数的最值不含参,属于中档题.
由已知分析可得发射B型号炮弹3发至少命中一发的概率为,则,计算即可;
由已知及全概率公式分析即可求解.
20.【答案】解:的概率分布列为
X1 12
P
,
设表示事件”第i次调整,价格下调”,则;
;,
故的概率分布列为
13 2
P
当时.,
由于
所以,当投资两个项目的利润均值相同的情况下,投资B项目的风险高于A项目.
从获得稳定收益考虑,当时应投资A项目.
【解析】本题考查离散型随机变量的分布列、期望与方差,考查利用概率知识解决实际问题,正确求期望与方差是关键.属于较难题.
根据的概率分布列,利用期望、方差公式,即可得到结论;
确定X的取值,求出相应的概率,可得的概率分布列;
当时,期望相同,利用方差的大小比较,即可得到结论.
21.【答案】解:由题意得,抽中的5人中消费金额为的人数为,
消费金额为的人数为,
设消费金额为的人数为X,则,
所以,,,
X的分布列为
X 1 2 3
P
则;
由题意得
,
所以,
所以;
由题意及得,
所以,,
,,
,
的分布列为
0 1 2 3 4
P
【解析】本题考查了正态分布的概率、方差、均值,是难题.
根据分层抽样分别求出消费金额为和抽取的人数,求出随机变量的可能取值,分别求出相应概率,进而求得分布列和数学期望;
求出,的值,结合正态分布求出概率;
由求出二项分布的分布列及方差
22.【答案】解:记“从10所学校中选出的3所学校参与“自由式滑雪”都超过40人”的事件为A;
参与“自由式滑雪”的人数超过40人的学校共4所,随机选择3所学校共种,
所以
的所有可能取值为0,1,2,3,参加“单板滑雪”人数在45人以上的学校共4所.
所以,,,
所以X的分布列为
X 0 1 2 3
P
所以
小明同学在一轮测试中为“优秀”的概率为:,
小明在n轮测试中获“优秀”次数满足,由,则,
所以理论上至少要进行20次测试.
【解析】本题主要考查了古典概型的计算与应用,离散型随机变量及其分布列与期望,考查了推理能力与计算能力,属于较难题.
利用组合数公式及古典概率公式求解即可;
由题意,可得X的所有可能取值为0,1,2,3,求出其对应的概率,进而求出数学期望即可;
求出集训前,小明同学总考核为“优秀”的概率,进而可得结论.
第20页,共20页
1. 设随机变量∽,∽,若,则的值为( )
A. B. C. D.
2. 某单位为了响应疫情期间有序复工复产的号召,组织从疫区回来的甲、乙、丙、丁4名员工进行核酸检测,现采用抽签法决定检测顺序,在“员工甲不是第一个检测,员工乙不是最后一个检测”的条件下,员工丙第一个检测的概率为( )
A. B. C. D.
3. 投壶是从先秦延续至清末的汉民族传统礼仪和宴饮游戏,在春秋战国时期较为盛行.如图为一幅唐朝的投壶图,假设甲、乙是唐朝的两位投壶游戏参与者,且甲、乙每次投壶投中的概率分别为,每人每次投壶相互独立.若约定甲投壶2次,乙投壶3次,投中次数多者胜,则甲最后获胜的概率为( )
A. B. C. D.
4. 根据国家关于加强禁毒教育要求,龙港中学举办了“禁毒知识竞赛”,采用抽题问答形式.设抽题盒中a道简单题,b道中等题,c道难题,且规定:抽中简单题并回答正确得1分,抽中中等题并回答正确得2分,抽中难题并回答正确得3分.现在从盒子中取出1道题并回答正确,记所得分为若,,则a:b:( )
A. 4:1:1 B. 5:2:1 C. 6:3:1 D. 6:3:2
5. 某卡车为乡村小学运送书籍,共装有10个纸箱,其中5箱英语书、2箱数学书、3箱语文书.到目的地时发现丢失一箱,但不知丢失哪一箱.现从剩下9箱中任意打开两箱,结果都是英语书,则丢失的一箱也是英语书的概率为( )
A. B. C. D.
6. 已知数列满足,且对任意,等概率地取或,设的值为随机变量,则( )
A. B.
C. D.
7. 托马斯贝叶斯在研究“逆向概率”的问题中得到了一个公式:,这个公式被称为贝叶斯公式贝叶斯定理,其中称为B的全概率.假设甲袋中有3个白球和3个红球,乙袋中有2个白球和2个红球.现从甲袋中任取2个球放入乙袋,再从乙袋中任取2个球.已知从乙袋中取出的是2个红球,则从甲袋中取出的也是2个红球的概率为( )
A. B. C. D.
8. 有甲、乙两个盒子,甲盒子里有1个红球,乙盒子里有3个红球和3个黑球,现从乙盒子里随机取出个球放入甲盒子后,再从甲盒子里随机取一球,记取到的红球个数为个,则随着的增加,下列说法正确的是( )
A. 增加,增加 B. 增加,减小
C. 减小,增加 D. 减小,减小
9. 已知,则( )
A. B. C. D.
10. 已知某校高三年级有1000人参加一次数学模拟考试,现把这次考试的分数转换为标准分,标准分的分数转换区间为,若使标准分X服从正态分布,参考数据:;;则
A. 这次考试标准分超过180分的约有450人
B. 这次考试标准分在内的人数约为997
C. 甲、乙、丙三人恰有2人的标准分超过180分的概率为
D.
11. 某市组织2022年度高中校园足球比赛,共有10支球队报名参赛.比赛开始前将这10支球队分成两个小组,每小组5支球队,其中获得2021年度冠、亚军的两支球队分别在第一小组和第二小组,剩余8支球队抽签分组.已知这8支球队中包含甲、乙两队,记“甲队分在第一小组”为事件,“乙队分在第一小组”为事件,“甲、乙两队分在同一小组”为事件,则( )
A. B.
C. D. 事件与事件相互独立
12. 一个袋子中装有除颜色外完全相同的10个球,其中有6个黑球,4个白球,现从中任取4个球,记随机变量X为取出白球的个数,随机变量Y为取出黑球的个数,若取出一个白球得2分,取出一个黑球得1分,随机变量Z为取出4个球的总得分,则下列结论中正确的是( )
A. B. C. D.
13. 勤洗手、常通风、戴口罩是切断新冠肺炎传播的有效手段.经调查疫情期间某小区居民人人养成了出门戴口罩的好习惯,且选择佩戴一次性医用口罩的概率为 p,每人是否选择佩戴一次性医用口罩是相互独立的.现随机抽取5 位该小区居民,其中选择佩戴一次性医用口罩的人数为 X,且,,则p的值为__________.
14. 抽样表明,某地区新生儿体重X近似服从正态分布假设随机抽取r个新生儿体检,记表示抽取的r个新生儿体重在以外的个数.若的数学期望,则r的最大值是__________.
注:若随机变量X∽,则
15. 一猎人带着一把猎枪到山里去打猎,猎枪每次可以装3发子弹,当他遇见一只野兔时,开第一枪命中野免的概率为,若第一枪没有命中,猎人开第二枪,命中野免的概率为,若第二枪也没有命中,猎人开第三枪,命中野兔的概率为,若3发子弹都没打中,野兔就逃跑了,则已知野兔被击中的条件下,是猎人开第二枪命中的概率为__________
16. 甲袋中有3个红球,2个白球和1个黑球,乙袋中有4个红球,1 个白球和1个黑球除颜色外,球的大小、形状完全相同先从甲袋中随机取出1球放入乙袋,再从乙袋中随机取出1球.分别以,,表示由甲袋取出的球是红球,白球和黑球的事件,以B表示由乙袋取出的球是红球的事件,则__________,__________.
17. 第24届冬季奥林匹克运动会于2022年2月在北京市和张家口市联合举行.甲、乙是单板滑雪坡面障碍技巧项目的参赛选手,二人在练习赛中均需要挑战3次某高难度动作,每次挑战的结果只有成功和失败两种.
甲在每次挑战中,成功的概率都为设X为甲在3次挑战中成功的次数,求X的分布列和数学期望;
乙在第一次挑战时,成功的概率为,受心理因素影响,从第二次开始,每次成功的概率会发生改变,其规律为:若前一次成功,则该次成功的概率比前一次成功的概率增加若前一次失败,则该次成功的概率比前一次成功的概率减少求乙在3次挑战中有且只有2次成功的条件下,第三次成功的概率.
18. 某单位有A,B两个餐厅为员工提供午餐与晚餐服务,甲、乙两位员工每个工作日午餐和晚餐都在单位就餐,近100个工作日选择餐厅就餐情况统计如下:
选择餐厅情况午餐,晚餐
甲员工 30天 20天 40天 10天
乙员工 20天 25天 15天 40天
假设甲、乙员工选择餐厅相互独立,用频率估计概率.
分别估计一天中甲员工午餐和晚餐都选择A餐厅就餐的概率,乙员工午餐和晚餐都选择B餐厅就餐的概率;
记X为甲、乙两员工在一天中就餐餐厅的个数,求X的分布列和数学期望;
试判断甲、乙员工在晚餐选择B餐厅就餐的条件下,哪位员工更有可能午餐选择A餐厅就餐,并说明理由.
19. 现有一种射击训练,每次训练都是由高射炮向目标飞行物连续发射三发炮弹,每发炮弹击中目标飞行物与否相互独立.已知射击训练有A,B两种型号的炮弹,对于A型号炮弹,每发炮弹击中目标飞行物的概率均为,且击中一弹目标飞行物坠毁的概率为,击中两弹目标飞行物必坠毁;对于B型号炮弹,每发炮弹击中目标飞行物的概率均为,且击中一弹目标飞行物坠毁的概率为,击中两弹目标飞行物坠毁的概率为,击中三弹目标飞行物必坠毁.
在一次训练中,使用B型号炮弹,求q满足什么条件时,才能使得至少有一发炮弹命中目标飞行物的概率不低于
若,试判断在一次训练中选用A型号炮弹还是B型号炮弹使得目标飞行物坠毁的概率更大 并说明理由.
20. 现有A,B两个项目,投资A项目100万元,一年后获得的利润为万元,根据市场分析,的概率分布列为
12
P
投资B项目100万元,一年后获得的利润万元与B项目产品价格的调整价格上调或下调有关已知产品价格在一年内进行2次独立的调整,且在每次调整中价格下调的概率都是经专家测算评估,B项目产品价格的下调次数与一年后获得相应利润的关系如下表所示:
B项目产品价格一年内下调的次数X 0 1 2
投资100万元一年后获得的利润万元 13 2
求的方差
求的分布列
若,根据投资获得利润的差异,你愿意选择投资哪个项目参考数据:
21. 为了深入贯彻党的十九大和十九届五中全会精神,坚持以新时代中国特色社会主义思想为指导,落实立德树人根本任务,着眼建设高质量教育体系,强化学校教育主阵地作用,深化校外培训机构治理,构建教育良好生态,有效缓解家长焦虑情绪,促进学生全面发展、健康成长.教育部门最近出台了“双减”政策,即有效减轻义务教育阶段学生过重作业负担和校外培训负担,持续规范校外培训包括线上培训和线下培训“双减”政策的出台对校外的培训机构经济效益产生了严重影响.某大型校外培训机构为了规避风险,寻求发展制定科学方案,工作人员对2020年的前200名报名学员消费等情况进行了统计整理,其中消费情况数据如表.
消费金额千元
人数 30 50 60 20 30 10
该大型校外培训机构转型方案之一是将文化科主阵地辅导培训向音体美等兴趣爱好培训转移,为了深入了解当前学生的兴趣爱好,工作人员利用分层抽样的方法在消费金额为和的学员中抽取了5人,再从这5人中选取3人进行有奖问卷调查,求抽取的3人中消费金额为的人数的分布列和数学期望;
以频率估计概率,假设该大型校外培训机构2020年所有学员的消费可视为服从正态分布,,分别为报名前200名学员消费的平均数以及方差同一区间的花费用区间的中点值替代
试估计该机构学员2020年消费金额为的概率保留一位小数;
若从该机构2020年所有学员中随机抽取4人,记消费金额为的人数为,求的分布列及方差.
参考数据:;若随机变量服从正态分布,则,,
22. 2022年冬季奥林匹克运动会主办城市是北京,北京成为第一个举办过夏季奥林匹克运动会和冬季奥林匹克运动会以及亚洲运动会三项国际赛事的城市!为迎接冬奥会的到来,某地很多中小学开展了模拟冬奥会赛事的活动,为了深入了解学生在“自由式滑雪”和“单板滑雪”两项活动的参与情况,在该地随机选取了10所学校进行研究,得到如下数据:
在这10所学校中随机选取3所来调查研究,求这3所学校参与“自由式滑雪”都超过40人的概率;
“单板滑雪”参与人数超过45人的学校可以作为“基地学校”,现在从这10所学校中随机选出3所,记X为选出可作“基地学校”的学校个数,求X的分布列和数学期望;
现在有一个“单板滑雪”集训营,对“滑行、转弯、停止”这3个动作技巧进行集训,且在集训中进行了多轮测试.规定:在一轮测试中,这3个动作中至少有2个动作达到“优秀”,则该轮测试记为“优秀”.在集训测试中,小明同学3个动作中每个动作达到“优秀”的概率均为,每个动作互不影响且每轮测试互不影响.如果小明同学在集训测试中要想获得“优秀”的次数的平均值达到5次,那么理论上至少要进行多少轮测试?
答案和解析
1.【答案】B
【解析】
【分析】
本题考查二项分布的概率计算,属于中档题.
首先根据求出p的值,再计算的值.
【解答】
解:因为随机变量,
所以,
解得,所以,
则
故选
2.【答案】B
【解析】
【分析】
本题考查应用概率解决实际问题,是基础题.
设员工甲不是第一个检测,员工乙不是最后一个检测为事件A,员工丙第一个检测为事件B,再对事件A发生的情况下发生事件B的概率进行分析,即可求解.
【解答】
解:设事件员工甲不是第一个检测,员工乙不是最后一个检测,事件员工丙第一个检测,
所以,
所以
故答案为
3.【答案】B
【解析】
【分析】
本题考查相互独立事件同时发生的概率,属于中档题.
由题可得甲最后获胜的情况有3种,分别求解概率再相加即得.
【解答】
解:由题意可得,甲、乙每次投壶投中的概率分别为,若约定甲投壶2次,乙投壶3次,投中次数多者胜,则甲最后获胜的情况有3种:
①甲投中1次,乙投中0次,则概率为
;
②甲投中2次,乙投中1次,则概率为
;
③甲投中2次,乙投中0次,则概率为
;
所以甲最后获胜的概率为
故选
4.【答案】B
【解析】
【分析】
由题意可得,所有可能的取值为1,2,3,分别求出对应的概率,再结合期望和方差的公式,即可求解.
本题主要考查期望与方差的公式,考查转化能力,属于中档题.
【解答】
解:由题意可得,所有可能的取值为1,2,3,
则,,,
,
,
所以,,即,,
故a:b::2:
故选:
5.【答案】B
【解析】
【分析】
本题考查贝叶斯公式的应用,考查全概率公式的应用,属于中档题.
A表示丢失一箱后任取两箱是英语书,用表示丢失的一箱为k,,2,3分别表示英语书、数学书、语文书.根据全概率公式求得,根据贝叶斯公式可得,进而得解.
【解答】
解:用A表示丢失一箱后任取两箱是英语书,用表示丢失的一箱为k,,2,3分别表示英语书、数学书、语文书.
由全概率公式得
故选
6.【答案】D
【解析】
【分析】
本题考查概率的求法,考查离散型随机变量的分布列、数学期望的求法,考查相互独立事件概率乘法公式等基础知识,考查运算求解能力,是中档题.
根据题意,分别分析出当n分别取2,3,4,5时所对应的值,以及每个的对应的概率,即可判断出正确选项.
【解答】
解:依题意或,且,
的可能取值为,,,,
,
,,
,
,
由此排除A和B;
的可能取值为,,,,,,
,
,
,
的可能取值为4,2,0,,
,
,
所以,排除
因为,,所以,
故选:
7.【答案】C
【解析】
【分析】
本题考查了条件概率,贝叶斯公式及古典概型,属于中档题.
根据题意,先分析求解设从甲袋中取出2个球,其中红球的个数为i个的事件为,事件的概率为,从乙袋中取出2个球,其中红球的个数为2个的事件为B,事件B的概率为,再分别分析三种情况求解即可.
【解答】
解:设从甲袋中取出2个球,其中红球的个数为i个的事件为,事件的概率为,从乙袋中取出2个球,其中红球的个数为2个的事件为B,事件B的概率为,由题意:
①,;
②,;
③,;
根据贝叶斯公式可得,从乙袋中取出的是2个红球,则从甲袋中取出的也是2个红球的概率为
故选:C
8.【答案】C
【解析】
【分析】
本题考查了超几何分布、两点分布,分布列与数学期望,考查了推理能力计算能力,属于难题.
依题意,从乙盒子里随机取出n个球,含有红球个数X服从超几何分布,即,故,再从乙盒子里随机取出n个球,含有红球个数X服从超几何分布,即,服从两点分布,所以 ,随着n的增大,减小;, 随着n的增大,增大;
【解答】
解:依题意,从乙盒子里随机取出n个球,含有红球个数X服从超几何分布,即,
其中 ,其中,且,
故从甲盒中取球,相当于从含有 个红球的个球中取一球,取到红球个数为个,
故,随着n的增大,减小;
,随着n的增大,增大;
故选
9.【答案】BCD
【解析】
【分析】
本题主要考查条件概率公式,全概率公式和事件公式,属于中档题;
根据条件概率公式,全概率公式和事件公式可逐一进行判断.
【解答】
解:对于B:, , 故选项CB正确;
对于C:,故选项 C正确;
对于A:由全概率公式得:
, ,
, 故选项A错;
对于D:,故选项 D正确;
故选:
10.【答案】BC
【解析】
【分析】
本题考查正态分布曲线性质及概率计算,属中档题目.
根据题意和正态分布的知识对选项逐一分析计算即可.
【解答】
解:由题意X服从正态分布,
,,故A不正确;
,,故B正确;
甲、乙、丙三人恰有2人的标准分超过180分的概率,故C正确;
因为,
,
所以 ,故D不正确.
故选
11.【答案】ABD
【解析】
【分析】
本题主要考查相互独立事件的概率乘法公式,古典概型,排列组合的应用,属于中档题.
根据已知条件,结合排列组合知识,以及相互独立事件的概率乘法公式,即可依次求解.
【解答】
解:对于A,甲队分在第一小组和第二小组的概率相等,且两种情况有且只有一种情况发生,
,故A正确,
对于B,8支球队抽签分组共有种不同方法,甲、乙两队分在同小组共有种不同方法,
所以甲,乙两队分在同一小组的概率,故B正确,
对于C,,
,故C错误,
对于D,,,
故,
故事件与事件相互独立,故D正确.
故选:
12.【答案】BD
【解析】
【分析】
本题主要考查超几何分布的概率和均值,属于较难题.
【解答】
解:随机变量X的所有可能取值为0,1,2,3,4,且服从超几何分布.
,,A错误.
,,
,
X 0 1 2 3 4
p
因此,
由题知,B正确.
故Y的分布列如下:
Y 0 1 2 3 4
p
因此
,C错误.
,D正确.
13.【答案】
【解析】
【分析】
本题主要考查了二项分布,属于基础题.
由题意,根据二项分布概率计算公式和方差公式计算出p值即可.
【解答】
解:由题意,,
且,
根据二项分布概率公式有,,
解得,
故,
则,
解得或舍去,
故答案为:
14.【答案】16
【解析】
【分析】
本题考查正态分布的概率计算,以及二项分布的期望公式,属于中档题.
根据正态分布的性质求出在之外的概率,从而得到 ,根据二项分布的期望公式得到不等式,解得即可.
【解答】
解:依题意,
所以在之外的概率,
则,
则,
因为,
所以,
解得 ,
因为 ,
所以r的最大值为
故答案为
15.【答案】
【解析】
【分析】
本题考查了互斥事件和条件概率,属于中档题.
利用互斥事件至少有一个发生的概率得“野兔被击中”的概率,再利用条件概率,计算得结论.
【解答】
解:设“猎人第一枪击中野兔”,“猎人第二枪击中野兔”,
“猎人第三枪击中野兔”,“野兔被击中”,
则互斥,且,,,
因此
,
所以
故答案为
16.【答案】
【解析】
【分析】
本题主要考查条件概率公式、全概率公式等基础知识,考查运算求解能力,属于中档题.
先分别求出,,再由,能求出;分别求出,,,,,,从而求出,,,再由,能求出
【解答】
解:甲袋中有3个红球,2个白球和1个黑球,乙袋中有4个红球,1个白球和1个黑球除颜色外,球的大小、形状完全相同
先从甲袋中随机取出1球放入乙袋,再从乙袋中随机取出1球.
分别以,,表示由甲袋取出的球是红球,白球和黑球的事件,以B表示由乙袋取出的球是红球的事件,
则,,
,
,,,
,,,
,,,
故答案为:;
17.【答案】解:由题意得,X∽,则,其中,1,2,3,
则X的分布列为:
X 0 1 2 3
P
则
设“乙在3次挑战中有且只有2次成功”,“乙在3次挑战中第三次成功”,
【解析】本题考查二项分布以及数学期望,考查条件概率的应用,考查了运算能力,属于中档题.
根据题意可得X∽,根据二项分布的概率以及期望公式即可求解;
根据条件概率的求法公式即可求解.
18.【答案】解:设事件C为“一天中甲员工午餐和晚餐都选择A餐厅就餐”,
事件D为“乙员工午餐和晚餐都选择B餐厅就餐”
因为100个工作日中甲员工午餐和晚餐都选择A餐厅就餐的天数为30,
乙员工午餐和晚餐都选择B餐厅就餐的天数为40,
所以,
由题意知,甲员工午餐和晚餐都选择B餐厅就餐的概率为,
乙员工午餐和晚餐都选择A餐厅就餐的概率为,
记X为甲、乙两员工在一天中就餐餐厅的个数,则X的所有可能取值为1、2,
所以,,
所以X的分布列为:
X 1 2
P
所以X的数学期望
设“甲员工晚餐选择B餐厅就餐”,“乙员工晚餐选择B餐厅就餐”,
“甲员工在午餐时选择A餐厅就餐”,“乙员工在午餐时选择A餐厅就餐”,
则,,因为,
所以在已知晚餐选择B 餐厅就餐的条件下,甲员工更有可能在午餐时选择 A餐厅就餐.
【解析】本题考查离散型随机变量的分布列和均值、古典概型及其计算、条件概率的概念与计算,属于中档题.
根据题意结合古典概型的概率公式,即可求出一天中甲员工午餐和晚餐都选择A餐厅就餐的概率,乙员工午餐和晚餐都选择B餐厅就餐的概率;
由题意确定X的所有可能取值为和对应概率,从而得到X的分布列,利用随机变量的期望公式求出;
利用条件概率公式分别求出“甲、乙员工在晚餐选择B餐厅就餐的条件下,午餐选择A餐厅就餐”的概率,比较二者概率大小即可判断哪位员工更有可能午餐选择A餐厅就餐.
19.【答案】解:因为发射B型号炮弹3发至少命中一发的对立事件是一发都未命中,且每发炮弹击中与否相互独立,
所以发射B型号炮弹3发至少命中一发的概率为,
所以,
解得,
所以,
选用B型号炮弹使得目标飞行物坠毁的概率更大,理由如下:
记事件“发射A型号炮弹目标飞行物坠毁”,“发射A型号炮弹命中i发”,
所以
,
同理记“发射B型号炮弹目标飞行物坠毁”,“发射B型号炮弹命中j发”,
所以
,
作差比较得,
记,则恒成立,
所以在上单调递减,
因为,
所以当时,,即,
所以选用B型号炮弹使得目标飞行物坠毁的概率更大.
【解析】本题主要考查相互独立事件的概率乘法公式,对立事件,互斥事件,全概率公式,利用导数求函数的最值不含参,属于中档题.
由已知分析可得发射B型号炮弹3发至少命中一发的概率为,则,计算即可;
由已知及全概率公式分析即可求解.
20.【答案】解:的概率分布列为
X1 12
P
,
设表示事件”第i次调整,价格下调”,则;
;,
故的概率分布列为
13 2
P
当时.,
由于
所以,当投资两个项目的利润均值相同的情况下,投资B项目的风险高于A项目.
从获得稳定收益考虑,当时应投资A项目.
【解析】本题考查离散型随机变量的分布列、期望与方差,考查利用概率知识解决实际问题,正确求期望与方差是关键.属于较难题.
根据的概率分布列,利用期望、方差公式,即可得到结论;
确定X的取值,求出相应的概率,可得的概率分布列;
当时,期望相同,利用方差的大小比较,即可得到结论.
21.【答案】解:由题意得,抽中的5人中消费金额为的人数为,
消费金额为的人数为,
设消费金额为的人数为X,则,
所以,,,
X的分布列为
X 1 2 3
P
则;
由题意得
,
所以,
所以;
由题意及得,
所以,,
,,
,
的分布列为
0 1 2 3 4
P
【解析】本题考查了正态分布的概率、方差、均值,是难题.
根据分层抽样分别求出消费金额为和抽取的人数,求出随机变量的可能取值,分别求出相应概率,进而求得分布列和数学期望;
求出,的值,结合正态分布求出概率;
由求出二项分布的分布列及方差
22.【答案】解:记“从10所学校中选出的3所学校参与“自由式滑雪”都超过40人”的事件为A;
参与“自由式滑雪”的人数超过40人的学校共4所,随机选择3所学校共种,
所以
的所有可能取值为0,1,2,3,参加“单板滑雪”人数在45人以上的学校共4所.
所以,,,
所以X的分布列为
X 0 1 2 3
P
所以
小明同学在一轮测试中为“优秀”的概率为:,
小明在n轮测试中获“优秀”次数满足,由,则,
所以理论上至少要进行20次测试.
【解析】本题主要考查了古典概型的计算与应用,离散型随机变量及其分布列与期望,考查了推理能力与计算能力,属于较难题.
利用组合数公式及古典概率公式求解即可;
由题意,可得X的所有可能取值为0,1,2,3,求出其对应的概率,进而求出数学期望即可;
求出集训前,小明同学总考核为“优秀”的概率,进而可得结论.
第20页,共20页
