人教版八年级数学下册18.2.1 第2课时 矩形的判定 教学课件(共20张PPT)
文档属性
| 名称 | 人教版八年级数学下册18.2.1 第2课时 矩形的判定 教学课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
18.2 特殊的平行四边形
18.2.1 矩 形
第十八章 平行四边形
课程讲授
新知导入
随堂练习
课堂小结
第2课时 矩形的判定
知识要点
1.有一个角是直角的平行四边形是矩形
2.对角线相等的平行四边形是矩形
3.有三个角是直角的四边形是矩形
新知导入
想一想:
问题2 矩形的性质有哪些?
问题1 矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
对边平行且相等.
四个角都是直角.
对角线互相平分且相等.
边:
角:
对角线:
课程讲授
1
有一个角是直角的平行四边形是矩形
归纳:方法一:有一个角是直角的平行四边形是矩形(定义法)
□ABCD
∠A=90°
四边形ABCD是矩形
课程讲授
练一练:
1
有一个角是直角的平行四边形是矩形
如图,在 ABCD中,E,F为BC上两点,且BE=CF,AF=DE.求证:四边形ABCD是矩形.
证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD.
∵BE=CF,∴BF=CE .
∵AF=DE,∴△ABF≌△DCE(SSS),∴∠B=∠C.
∵AB∥CD,∴∠B+∠C=180°,
∴∠B=∠C=90°,
∴ ABCD是矩形.
课程讲授
2
对角线相等的平行四边形是矩形
想一想:我们知道,矩形的对角线相等.反过来,对角
线相等的平行四边形是矩形吗?
工人师傅在做门窗或矩形零件时,不
仅要测量两组对边的长度是否分别相等,
常常还要测量它们的两条对角线是否相等,
以确保图形是矩形.你知道其中的道理吗?
猜想:对角线相等的平行四边形是矩形
课程讲授
2
对角线相等的平行四边形是矩形
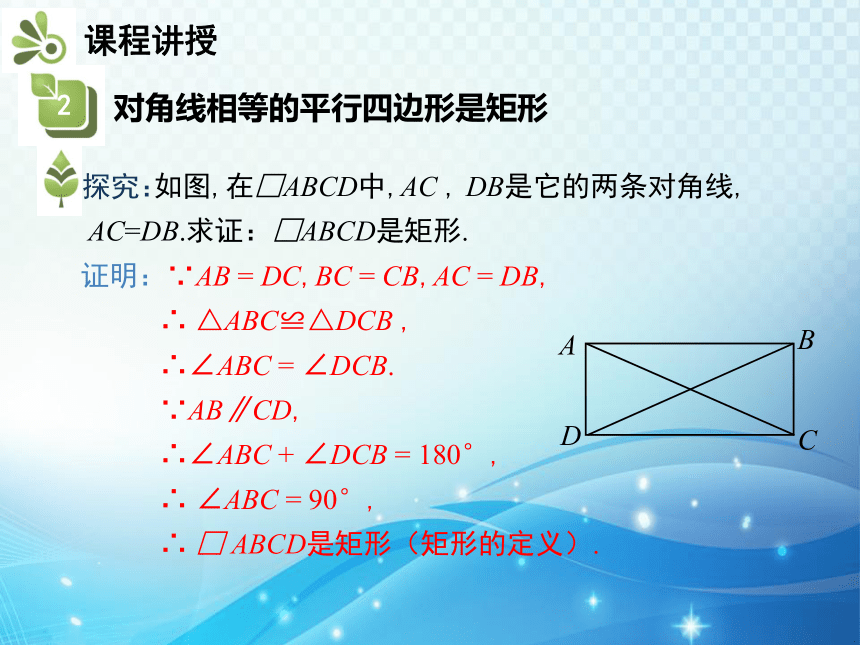
探究:
如图,在□ABCD中,AC , DB是它的两条对角线,
AC=DB.求证:□ABCD是矩形.
证明:∵AB = DC,BC = CB,AC = DB,
∴ △ABC≌△DCB ,
∴∠ABC = ∠DCB.
∵AB∥CD,
∴∠ABC + ∠DCB = 180°,
∴ ∠ABC = 90°,
∴ □ ABCD是矩形(矩形的定义).
A
B
C
D
2
对角线相等的平行四边形是矩形
课程讲授
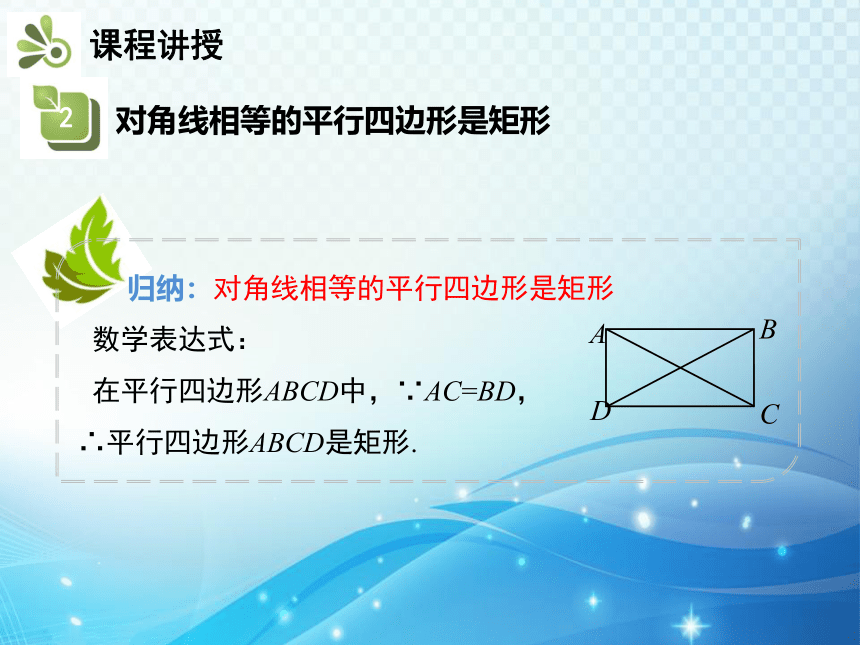
归纳:对角线相等的平行四边形是矩形
数学表达式:
在平行四边形ABCD中,∵AC=BD,
∴平行四边形ABCD是矩形.
A
B
C
D
2
对角线相等的平行四边形是矩形
课程讲授
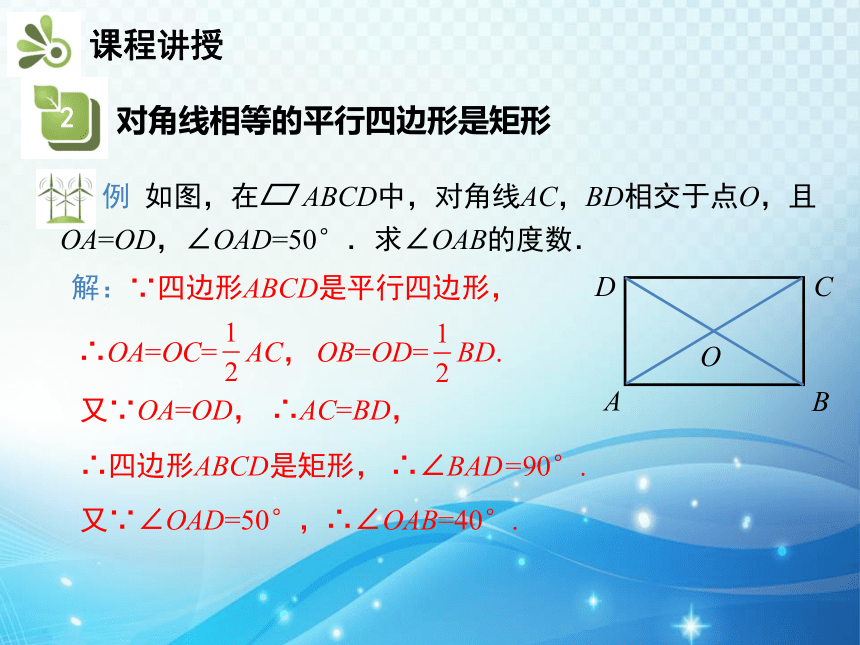
例 如图,在 ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
∴OA=OC= AC,
OB=OD= BD.
又∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°.
又∵∠OAD=50°,
∴∠OAB=40°.
2
对角线相等的平行四边形是矩形
课程讲授
练一练:
如图,要使 ABCD成为矩形,需添加的条件是( )
A.AB=BC
B.AO=BO
C.∠1=∠2
D.AC⊥BD
B
课程讲授
3
有三个角是直角的四边形是矩形
想一想: 前面我们研究了矩形的四个角,知道它们都是直角.它的逆命题成立吗?即四个角都是直角的四
边形是矩形吗?进一步,至少有几个角是直角的四
边形是矩形?
猜想:有三个角是直角的四边形是矩形
课程讲授
3
有三个角是直角的四边形是矩形
探究:
如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
A
B
C
D
3
有三个角是直角的四边形是矩形
课程讲授
归纳:有三个角是直角的四边形是矩形
数学表达式:
在四边形ABCD中,
∵ ∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
A
B
C
D
课程讲授
3
有三个角是直角的四边形是矩形
练一练:
如图,在平行四边形ABCD中,AE=CF,AG⊥DE,CH⊥BF,求证:四边形EHFG是矩形.
证明:∵四边形ABCD是平行四边形,
∴AE∥CF .
∵AE=CF,
∴四边形AECF是平行四边形,
∴AF∥EC,∴∠FGE+∠GEH=180°.
又∵AG⊥DE,CH⊥BF,
∴∠FGE=∠EHF=90°,∴∠GEH=90°
∴四边形EHFG是矩形.
随堂练习
1.下列命题中,真命题有( )
(1)对角线互相平分的四边形是矩形
(2)三个角的度数之比为1:3 :4的三角形是直角三角形
(3)对角互补的平行四边形是矩形
(4)三边之比为1: :2的三角形是直角三角形
A.1个 B.2个 C.3个 D.4个
C
随堂练习
2.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A.AB∥DC
B.AC=BD
C.AC⊥BD
D.AB=DC
C
随堂练习
3.(中考·龙东)如图,在 ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB,请你添加一个条件______________________,使四边形DBCE是矩形.
EB=DC(答案不唯一)
随堂练习
4.如图,在△ABC中,AB=AC,AD是BC边上的高,AE是△BAC的外角平分线,DE∥AB交AE于点E,求证:四边形ADCE是矩形.
随堂练习
证明:∵AB=AC,AD⊥BC,∴∠B=∠ACB,BD=DC.
∵AE是∠BAC的外角平分线,
∴∠FAE=∠EAC.
∵∠B+∠ACB=∠FAE+∠EAC,
∴∠B=∠ACB=∠FAE=∠EAC,
∴AE∥CD.
又∵DE∥AB,∴四边形AEDB是平行四边形,
∴AE BD.又∵BD=DC,
∴AE DC,
∴四边形ADCE是平行四边形.
又∵∠ADC=90°,
∴平行四边形ADCE是矩形.
∥
=
∥
=
课堂小结
矩形的判定
定义法:有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
18.2 特殊的平行四边形
18.2.1 矩 形
第十八章 平行四边形
课程讲授
新知导入
随堂练习
课堂小结
第2课时 矩形的判定
知识要点
1.有一个角是直角的平行四边形是矩形
2.对角线相等的平行四边形是矩形
3.有三个角是直角的四边形是矩形
新知导入
想一想:
问题2 矩形的性质有哪些?
问题1 矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
对边平行且相等.
四个角都是直角.
对角线互相平分且相等.
边:
角:
对角线:
课程讲授
1
有一个角是直角的平行四边形是矩形
归纳:方法一:有一个角是直角的平行四边形是矩形(定义法)
□ABCD
∠A=90°
四边形ABCD是矩形
课程讲授
练一练:
1
有一个角是直角的平行四边形是矩形
如图,在 ABCD中,E,F为BC上两点,且BE=CF,AF=DE.求证:四边形ABCD是矩形.
证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD.
∵BE=CF,∴BF=CE .
∵AF=DE,∴△ABF≌△DCE(SSS),∴∠B=∠C.
∵AB∥CD,∴∠B+∠C=180°,
∴∠B=∠C=90°,
∴ ABCD是矩形.
课程讲授
2
对角线相等的平行四边形是矩形
想一想:我们知道,矩形的对角线相等.反过来,对角
线相等的平行四边形是矩形吗?
工人师傅在做门窗或矩形零件时,不
仅要测量两组对边的长度是否分别相等,
常常还要测量它们的两条对角线是否相等,
以确保图形是矩形.你知道其中的道理吗?
猜想:对角线相等的平行四边形是矩形
课程讲授
2
对角线相等的平行四边形是矩形
探究:
如图,在□ABCD中,AC , DB是它的两条对角线,
AC=DB.求证:□ABCD是矩形.
证明:∵AB = DC,BC = CB,AC = DB,
∴ △ABC≌△DCB ,
∴∠ABC = ∠DCB.
∵AB∥CD,
∴∠ABC + ∠DCB = 180°,
∴ ∠ABC = 90°,
∴ □ ABCD是矩形(矩形的定义).
A
B
C
D
2
对角线相等的平行四边形是矩形
课程讲授
归纳:对角线相等的平行四边形是矩形
数学表达式:
在平行四边形ABCD中,∵AC=BD,
∴平行四边形ABCD是矩形.
A
B
C
D
2
对角线相等的平行四边形是矩形
课程讲授
例 如图,在 ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
∴OA=OC= AC,
OB=OD= BD.
又∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°.
又∵∠OAD=50°,
∴∠OAB=40°.
2
对角线相等的平行四边形是矩形
课程讲授
练一练:
如图,要使 ABCD成为矩形,需添加的条件是( )
A.AB=BC
B.AO=BO
C.∠1=∠2
D.AC⊥BD
B
课程讲授
3
有三个角是直角的四边形是矩形
想一想: 前面我们研究了矩形的四个角,知道它们都是直角.它的逆命题成立吗?即四个角都是直角的四
边形是矩形吗?进一步,至少有几个角是直角的四
边形是矩形?
猜想:有三个角是直角的四边形是矩形
课程讲授
3
有三个角是直角的四边形是矩形
探究:
如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
A
B
C
D
3
有三个角是直角的四边形是矩形
课程讲授
归纳:有三个角是直角的四边形是矩形
数学表达式:
在四边形ABCD中,
∵ ∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
A
B
C
D
课程讲授
3
有三个角是直角的四边形是矩形
练一练:
如图,在平行四边形ABCD中,AE=CF,AG⊥DE,CH⊥BF,求证:四边形EHFG是矩形.
证明:∵四边形ABCD是平行四边形,
∴AE∥CF .
∵AE=CF,
∴四边形AECF是平行四边形,
∴AF∥EC,∴∠FGE+∠GEH=180°.
又∵AG⊥DE,CH⊥BF,
∴∠FGE=∠EHF=90°,∴∠GEH=90°
∴四边形EHFG是矩形.
随堂练习
1.下列命题中,真命题有( )
(1)对角线互相平分的四边形是矩形
(2)三个角的度数之比为1:3 :4的三角形是直角三角形
(3)对角互补的平行四边形是矩形
(4)三边之比为1: :2的三角形是直角三角形
A.1个 B.2个 C.3个 D.4个
C
随堂练习
2.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A.AB∥DC
B.AC=BD
C.AC⊥BD
D.AB=DC
C
随堂练习
3.(中考·龙东)如图,在 ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB,请你添加一个条件______________________,使四边形DBCE是矩形.
EB=DC(答案不唯一)
随堂练习
4.如图,在△ABC中,AB=AC,AD是BC边上的高,AE是△BAC的外角平分线,DE∥AB交AE于点E,求证:四边形ADCE是矩形.
随堂练习
证明:∵AB=AC,AD⊥BC,∴∠B=∠ACB,BD=DC.
∵AE是∠BAC的外角平分线,
∴∠FAE=∠EAC.
∵∠B+∠ACB=∠FAE+∠EAC,
∴∠B=∠ACB=∠FAE=∠EAC,
∴AE∥CD.
又∵DE∥AB,∴四边形AEDB是平行四边形,
∴AE BD.又∵BD=DC,
∴AE DC,
∴四边形ADCE是平行四边形.
又∵∠ADC=90°,
∴平行四边形ADCE是矩形.
∥
=
∥
=
课堂小结
矩形的判定
定义法:有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
