人教版八年级数学下册 第18章 平行四边形 整合与提升 教学课件(共27张PPT)
文档属性
| 名称 | 人教版八年级数学下册 第18章 平行四边形 整合与提升 教学课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 00:00:00 | ||
图片预览

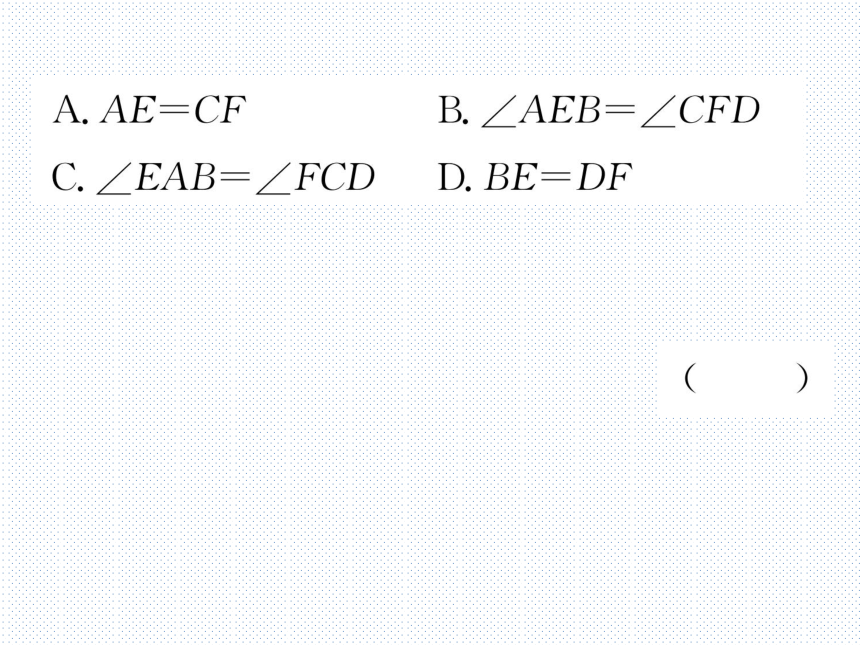



文档简介
(共27张PPT)
高频考点助力中考
考点①平行四边形的性质与判定
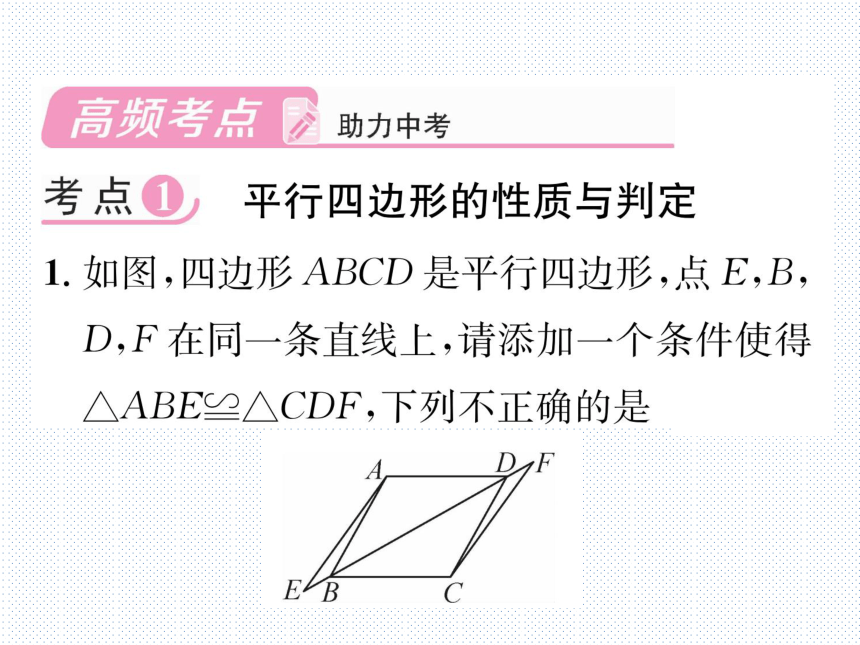
1.如图,四边形ABCD是平行四边形,点E,B,
D,F在同一条直线上,请添加一个条件使得
△ABE≌△CDF,下列不正确的是(A)
A.AE-CF
B.∠AEB=∠CFD
C.∠EAB=∠FCD
D.BE-DF
(第1题图)
(第2题图)
2.(2021·天津中考)如图, ABCD的顶点
A,B,C的坐标分别是(0,1),(一2,一2),(2,
一2),则顶点D的坐标是
(C)
A.(-4,1)
B.(4,-2)
C.(4,1)
D.(2,1)
3.(2021·宁波中若)如图,
在△ABC中,∠B=45°,
∠C=60°,AD⊥BC于
、B
FD
D,BD=√3.若E,F分别为AB,BC的中点,
则EF的长为
(C)
号
号
C.1
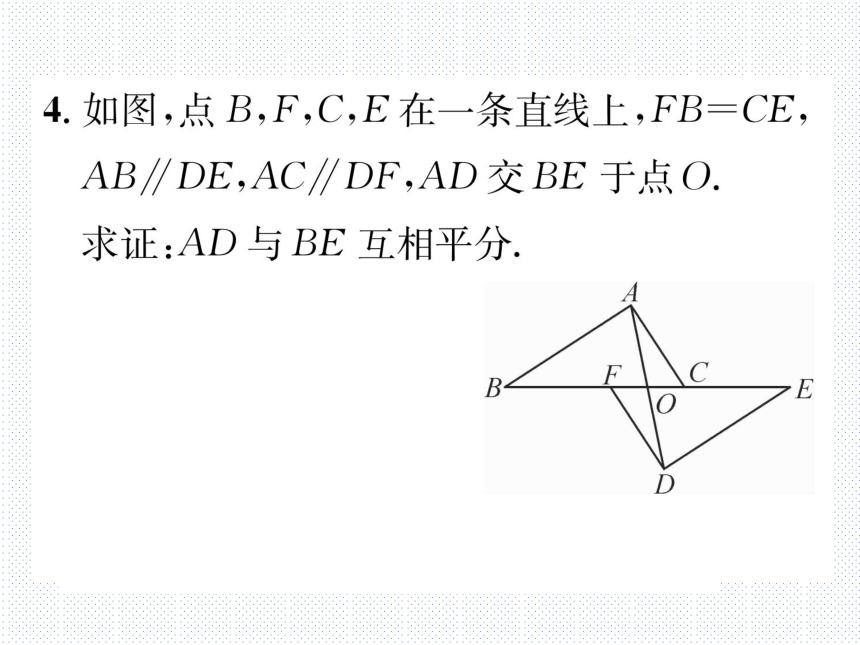
4.如图,点B,F,C,E在一条直线上,FB=CE
AB∥DE,AC∥DF,AD交BE于点O.
求证:AD与BE互相平分
证明:连接AE,BD.
.'FB=CE,..FB+FC=
CE+FC,即BC=EF.
AB∥DE,∴.∠ABC=
∠DEF..'AC∥DF,∴.∠ACB=∠DFE
∠ABC=∠DEF,
在△ABC和△DEF中,BC=EF,
∠ACB=∠DFE,
A
C
B
0
E
D
.∧ABC2△DEF(ASA),.'.AB=DE.
又.AB∥DE,.四边形ABDE是平行四边形,
,'.AD与BE互相平分.
考点②
特殊平行四边形的性质与判定
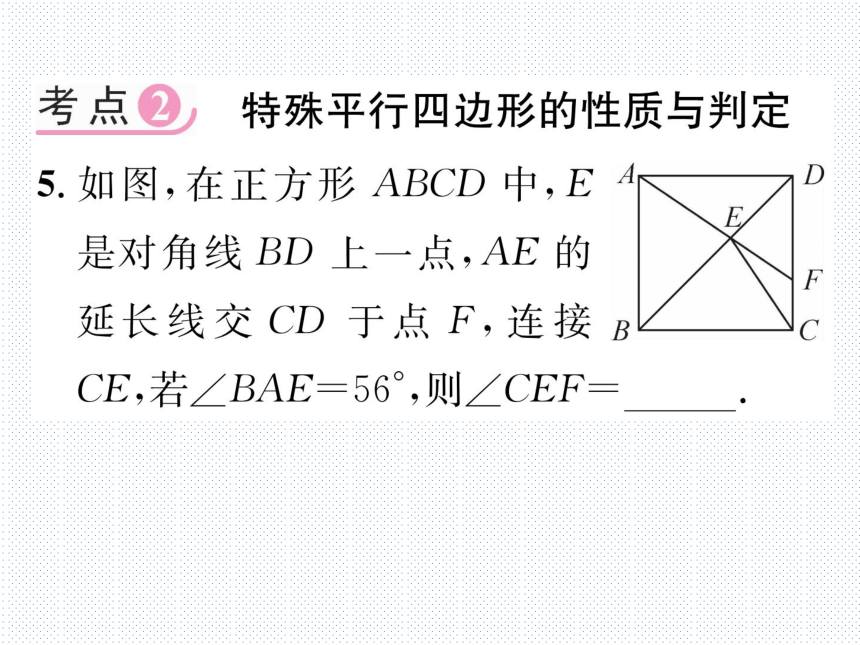
5.如图,在正方形ABCD中,E
E
是对角线BD上一点,AE的
F
延长线交CD于点F,连接B
C
CE,若∠BAE=56°,则∠CEF=
22°
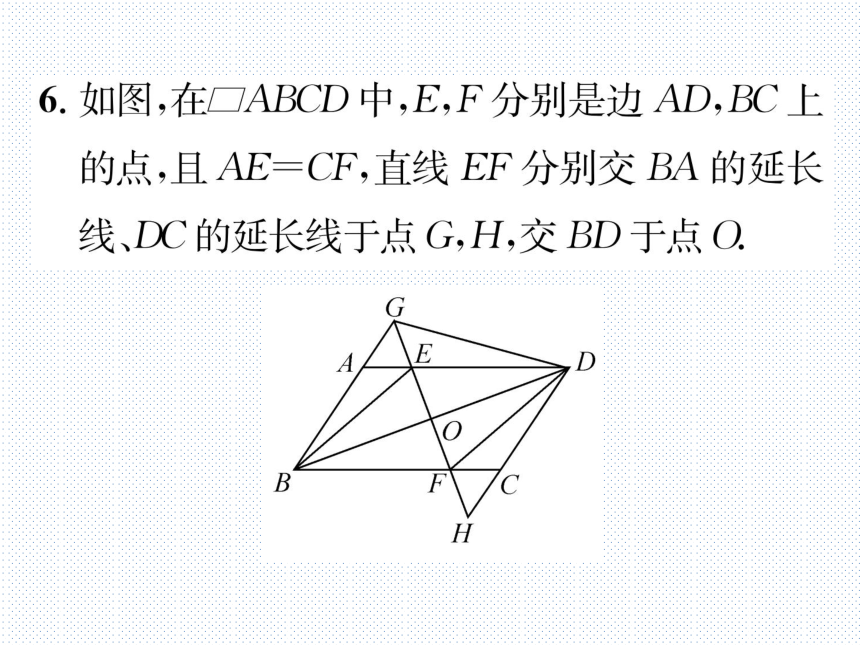
6.如图,在□ABCD中,E,F分别是边AD,BC上
的点,且AE=CF,直线EF分别交BA的延长
线、DC的延长线于点G,H,交BD于点O
(1)求证:∧ABE≌∧CDF:
(2)连接DG,若DG=BG,则四边形BEDF
是什么特殊四边形?请说明理由
解:(1).四边形ABCD是亚行四边形,
.AB=CD,∠BAE=∠DCF.
在△ABE知△CDF中,
AB=CD,
E
BAE-DCF,
AE=CF,
B
.'.∧ABE≌∧CDF(SAS);
H
(2)四边形BEDF是菱形.理由如下:
.四边形ABCD是平行四边形,
.AD=BC,AD∥BC.
.AE=CF,.AD-AE=BC-CF,月即DE=BF,
.四边形BEDF是平行四边形,.BO=DO,
在△BGD中,.BG=DG,BO=DO,.GO⊥BD,
∴.四边形BEDF是菱形.
高频考点助力中考
考点①平行四边形的性质与判定
1.如图,四边形ABCD是平行四边形,点E,B,
D,F在同一条直线上,请添加一个条件使得
△ABE≌△CDF,下列不正确的是(A)
A.AE-CF
B.∠AEB=∠CFD
C.∠EAB=∠FCD
D.BE-DF
(第1题图)
(第2题图)
2.(2021·天津中考)如图, ABCD的顶点
A,B,C的坐标分别是(0,1),(一2,一2),(2,
一2),则顶点D的坐标是
(C)
A.(-4,1)
B.(4,-2)
C.(4,1)
D.(2,1)
3.(2021·宁波中若)如图,
在△ABC中,∠B=45°,
∠C=60°,AD⊥BC于
、B
FD
D,BD=√3.若E,F分别为AB,BC的中点,
则EF的长为
(C)
号
号
C.1
4.如图,点B,F,C,E在一条直线上,FB=CE
AB∥DE,AC∥DF,AD交BE于点O.
求证:AD与BE互相平分
证明:连接AE,BD.
.'FB=CE,..FB+FC=
CE+FC,即BC=EF.
AB∥DE,∴.∠ABC=
∠DEF..'AC∥DF,∴.∠ACB=∠DFE
∠ABC=∠DEF,
在△ABC和△DEF中,BC=EF,
∠ACB=∠DFE,
A
C
B
0
E
D
.∧ABC2△DEF(ASA),.'.AB=DE.
又.AB∥DE,.四边形ABDE是平行四边形,
,'.AD与BE互相平分.
考点②
特殊平行四边形的性质与判定
5.如图,在正方形ABCD中,E
E
是对角线BD上一点,AE的
F
延长线交CD于点F,连接B
C
CE,若∠BAE=56°,则∠CEF=
22°
6.如图,在□ABCD中,E,F分别是边AD,BC上
的点,且AE=CF,直线EF分别交BA的延长
线、DC的延长线于点G,H,交BD于点O
(1)求证:∧ABE≌∧CDF:
(2)连接DG,若DG=BG,则四边形BEDF
是什么特殊四边形?请说明理由
解:(1).四边形ABCD是亚行四边形,
.AB=CD,∠BAE=∠DCF.
在△ABE知△CDF中,
AB=CD,
E
BAE-DCF,
AE=CF,
B
.'.∧ABE≌∧CDF(SAS);
H
(2)四边形BEDF是菱形.理由如下:
.四边形ABCD是平行四边形,
.AD=BC,AD∥BC.
.AE=CF,.AD-AE=BC-CF,月即DE=BF,
.四边形BEDF是平行四边形,.BO=DO,
在△BGD中,.BG=DG,BO=DO,.GO⊥BD,
∴.四边形BEDF是菱形.
