人教版八年级数学下册18.1.2 第3课时 三角形的中位线 教学课件(共13张PPT)
文档属性
| 名称 | 人教版八年级数学下册18.1.2 第3课时 三角形的中位线 教学课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-03 05:43:13 | ||
图片预览



文档简介
(共13张PPT)
18.1 平行四边形
18.1.2 平行四边形的判定
第十八章 平行四边形
课程讲授
新知导入
随堂练习
课堂小结
第3课时 三角形的中位线
知识要点
三角形的中位线
新知导入
想一想:平行四边形的判定有哪些?
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
新知导入
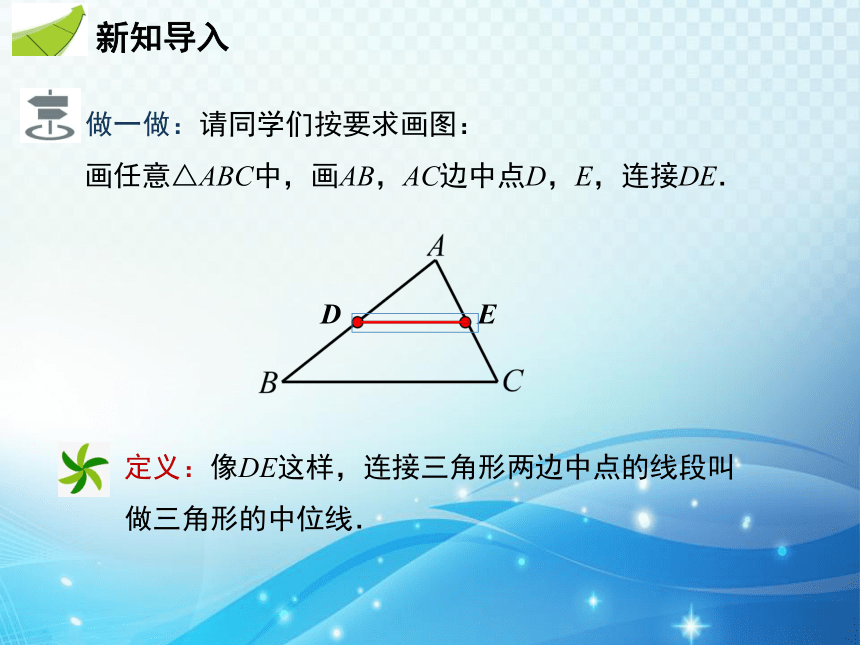
做一做:请同学们按要求画图:
画任意△ABC中,画AB,AC边中点D,E,连接DE.
定义:像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
D
E
课程讲授
1
三角形的中位线
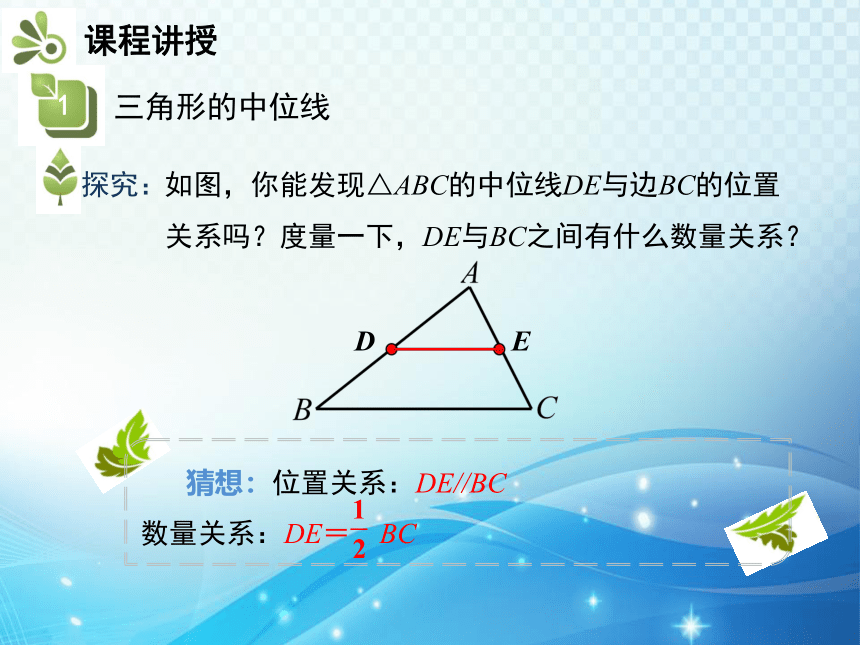
探究:
如图,你能发现△ABC的中位线DE与边BC的位置关系吗?度量一下,DE与BC之间有什么数量关系?
D
E
猜想:位置关系:DE//BC
数量关系:DE= BC
课程讲授
1
三角形的中位线
探究:
如图,D,E分别是△ABC的AB,AC的中点.
求证:DE//BC, DE= BC.
D
E
F
如图,延长DE到点F,使EF=DE,连接FC,
DC,AF. ∵AE=EC,DE=EF,
∴四边形ADCF是平行四边形,
CF DA.∴CF BD.
∴四边形DBCF是平行四边形,DF BC.
又 ∵DE= DF,
∴ DE//BC,且DE= BC.
证明:
∥
=
∥
=
∥
=
1
三角形的中位线
课程讲授
归纳:通过上述证明,我们得到三角形的中位线定理:
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
课程讲授
练一练:
1
三角形的中位线
(中考·梧州)如图,在△ABC中,AB=3,BC=4,AC=2,D,E,F分别为AB,BC,AC的中点,连接DF,FE,则四边形DBEF的周长是( )
A.5
B.7
C.9
D.11
B
随堂练习
1.( 中考·宜昌)如图,要测定被池塘隔开的A,B两点的距离,可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接ED. 现测得AC=30 m,BC=40 m,DE=24 m,则AB=( )
A.50 m
B.48 m
C.45 m
D.35 m
B
随堂练习
2.(中考·营口)如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )
A.∠ECD=112.5°
B.DE平分∠FDC
C.∠DEC=30°
D.AB= CD
C
随堂练习
3.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3.
(1)求证:BN=DN;
(2)求△ABC的周长.
(1)证明:
∵AN平分∠BAC,∴∠1=∠2.
∵BN⊥AN,∴∠ANB=∠AND=90°.
在△ABN和△ADN中,
∠1=∠2,
AN=AN,
∠ANB=∠AND,
∴△ABN ≌△ADN(ASA).
∴BN=DN.
随堂练习
(2)解:∵△ABN≌△ADN,
∴AD=AB=10,DN=NB.
又∵点M是BC中点,
∴MN是△BDC的中位线.
∴CD=2MN=6.
∴△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.
课堂小结
三角形的中位线
三角形的中位线定理
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
18.1 平行四边形
18.1.2 平行四边形的判定
第十八章 平行四边形
课程讲授
新知导入
随堂练习
课堂小结
第3课时 三角形的中位线
知识要点
三角形的中位线
新知导入
想一想:平行四边形的判定有哪些?
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
新知导入
做一做:请同学们按要求画图:
画任意△ABC中,画AB,AC边中点D,E,连接DE.
定义:像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
D
E
课程讲授
1
三角形的中位线
探究:
如图,你能发现△ABC的中位线DE与边BC的位置关系吗?度量一下,DE与BC之间有什么数量关系?
D
E
猜想:位置关系:DE//BC
数量关系:DE= BC
课程讲授
1
三角形的中位线
探究:
如图,D,E分别是△ABC的AB,AC的中点.
求证:DE//BC, DE= BC.
D
E
F
如图,延长DE到点F,使EF=DE,连接FC,
DC,AF. ∵AE=EC,DE=EF,
∴四边形ADCF是平行四边形,
CF DA.∴CF BD.
∴四边形DBCF是平行四边形,DF BC.
又 ∵DE= DF,
∴ DE//BC,且DE= BC.
证明:
∥
=
∥
=
∥
=
1
三角形的中位线
课程讲授
归纳:通过上述证明,我们得到三角形的中位线定理:
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
课程讲授
练一练:
1
三角形的中位线
(中考·梧州)如图,在△ABC中,AB=3,BC=4,AC=2,D,E,F分别为AB,BC,AC的中点,连接DF,FE,则四边形DBEF的周长是( )
A.5
B.7
C.9
D.11
B
随堂练习
1.( 中考·宜昌)如图,要测定被池塘隔开的A,B两点的距离,可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接ED. 现测得AC=30 m,BC=40 m,DE=24 m,则AB=( )
A.50 m
B.48 m
C.45 m
D.35 m
B
随堂练习
2.(中考·营口)如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )
A.∠ECD=112.5°
B.DE平分∠FDC
C.∠DEC=30°
D.AB= CD
C
随堂练习
3.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3.
(1)求证:BN=DN;
(2)求△ABC的周长.
(1)证明:
∵AN平分∠BAC,∴∠1=∠2.
∵BN⊥AN,∴∠ANB=∠AND=90°.
在△ABN和△ADN中,
∠1=∠2,
AN=AN,
∠ANB=∠AND,
∴△ABN ≌△ADN(ASA).
∴BN=DN.
随堂练习
(2)解:∵△ABN≌△ADN,
∴AD=AB=10,DN=NB.
又∵点M是BC中点,
∴MN是△BDC的中位线.
∴CD=2MN=6.
∴△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.
课堂小结
三角形的中位线
三角形的中位线定理
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
