6.4.3正弦定理 课件(共23张PPT)
文档属性
| 名称 | 6.4.3正弦定理 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 17:00:39 | ||
图片预览







文档简介
(共23张PPT)
2019年人教A版高中数学必修一
正弦定理
南宁市华侨实验高中 xx
我们离月球究竟有多远
世界第一高桥——北盘江大桥有多高呢?
1
2
3
4
三角的关系:
三边的关系:
边角的关系:
初中解三角形的有关知识
元素:
三个角,三条边
大边对大角,小边对小角
回顾旧知:
A
C
c
b
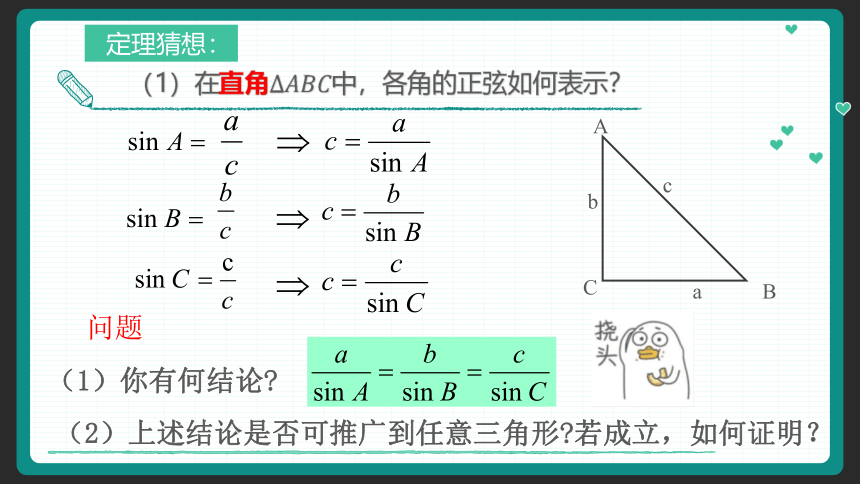
问题
(2)上述结论是否可推广到任意三角形 若成立,如何证明?
(1)你有何结论
定理猜想:
B
a
(1)在直角各角的正弦如何表示?
所以AD=csinB=bsinC, 即
同理可得
D
A
c
b
C
B
图1
过点A作AD⊥BC于D,
此时有
(2)若三角形是锐角三角形, 如图1,
正弦定理证明:
(任意三角形转化为直角三角形中的边角关系)
即:
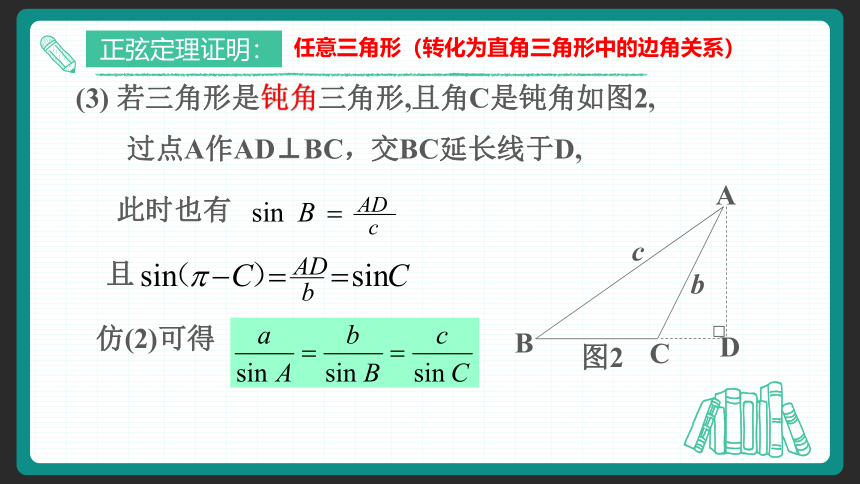
且
仿(2)可得
D
(3) 若三角形是钝角三角形,且角C是钝角如图2,
此时也有
交BC延长线于D,
过点A作AD⊥BC,
C
A
c
b
B
图2
正弦定理证明:
任意三角形(转化为直角三角形中的边角关系)
(1)文字叙述:在一个三角形中,各边和它所对角的正弦 的比相等.
(2)结构特点:
和谐美 、对称美 .
正弦定理:
定理构建:
正弦定理:
正弦定理及其变形:
变形:① a=_______,b=_______,c=________.
②a∶b∶c=_______________.
③sin A=______,sin B=______,sin C=______.
④ =_______ =_________
sin A∶sin B∶sin C
2Rsin B
2Rsin C
2Rsin A
正弦定理可以解决解三角形中的以下问题:
①
已知两角和一边,求其他角和边
②
已知两边和其中一边的对角,求另一边的对角进而可求其他的边和角
正弦定理适用范围:
在 中,角A,B,C的对边分别是a,b,c,且
解三角形。
解:由正弦定理 得:
例 1:
正弦定理的应用一:
(1)已知两角和任意一边,求其余两边和一角
练习1 在△ABC 中,已知c = 10, A = 45。, C = 30。求 a , b.
解:
且
∵
∴
b =
=
∵
∴
a =
=
B
A
C
b
c
a
例 2
已知a=16, b= , A=30° .求角B,C和边c
解:由正弦定理
得
所以
B=60°,
或B=120°
当 时
B=60°
当B=120°时
C=180°-A-B=30°
C=180°-A-B=90°
正弦定理应用二:
已知两边及其中一边的对角
解:由正弦定理
得
所以
B=60°,
或B=120°
当 时
B=60°
C=180°-A-B=30°
当B=120°时
300
A
B
C
16
3
16
∵ b > a ∴ B > A ,
C=180°-A-B=90°
16
B
三角形中大边对大角
已知a=16, b= , A=30° .求角B,C和边c
例 2
所以
B=300,
或B=1500
由于1500 +450>1800
故B只有一解 (如图)
C=1050,
练习2: a=4, b= , A=45°求角B,C和边c
解:由正弦定理
得
450
A
B
C
4
三角形中大边对大角
A
B
C
α
β
地月距离如何测量呢?
构造三角形。
A
B
C
α
β
一个定理:正弦定理
两类应用
(1)已知两角及一边,解三角形
(2)已知两边及一边的对角,解三角形(要注意多解)
谈谈你这节课学到了什么?
三种思想
(1)从特殊到一般的思想方法
(2)分类讨论的思想
(3)化归思想
课堂小结:
必做题:1、课本P48第1、2 、3题
2、教辅P30例1、例2、例3
作业布置:
选做题:思考其他证明正弦定理的方法。
南宁市华侨实验高中 xx
2019年人教A版高中数学必修一
正弦定理
南宁市华侨实验高中 xx
我们离月球究竟有多远
世界第一高桥——北盘江大桥有多高呢?
1
2
3
4
三角的关系:
三边的关系:
边角的关系:
初中解三角形的有关知识
元素:
三个角,三条边
大边对大角,小边对小角
回顾旧知:
A
C
c
b
问题
(2)上述结论是否可推广到任意三角形 若成立,如何证明?
(1)你有何结论
定理猜想:
B
a
(1)在直角各角的正弦如何表示?
所以AD=csinB=bsinC, 即
同理可得
D
A
c
b
C
B
图1
过点A作AD⊥BC于D,
此时有
(2)若三角形是锐角三角形, 如图1,
正弦定理证明:
(任意三角形转化为直角三角形中的边角关系)
即:
且
仿(2)可得
D
(3) 若三角形是钝角三角形,且角C是钝角如图2,
此时也有
交BC延长线于D,
过点A作AD⊥BC,
C
A
c
b
B
图2
正弦定理证明:
任意三角形(转化为直角三角形中的边角关系)
(1)文字叙述:在一个三角形中,各边和它所对角的正弦 的比相等.
(2)结构特点:
和谐美 、对称美 .
正弦定理:
定理构建:
正弦定理:
正弦定理及其变形:
变形:① a=_______,b=_______,c=________.
②a∶b∶c=_______________.
③sin A=______,sin B=______,sin C=______.
④ =_______ =_________
sin A∶sin B∶sin C
2Rsin B
2Rsin C
2Rsin A
正弦定理可以解决解三角形中的以下问题:
①
已知两角和一边,求其他角和边
②
已知两边和其中一边的对角,求另一边的对角进而可求其他的边和角
正弦定理适用范围:
在 中,角A,B,C的对边分别是a,b,c,且
解三角形。
解:由正弦定理 得:
例 1:
正弦定理的应用一:
(1)已知两角和任意一边,求其余两边和一角
练习1 在△ABC 中,已知c = 10, A = 45。, C = 30。求 a , b.
解:
且
∵
∴
b =
=
∵
∴
a =
=
B
A
C
b
c
a
例 2
已知a=16, b= , A=30° .求角B,C和边c
解:由正弦定理
得
所以
B=60°,
或B=120°
当 时
B=60°
当B=120°时
C=180°-A-B=30°
C=180°-A-B=90°
正弦定理应用二:
已知两边及其中一边的对角
解:由正弦定理
得
所以
B=60°,
或B=120°
当 时
B=60°
C=180°-A-B=30°
当B=120°时
300
A
B
C
16
3
16
∵ b > a ∴ B > A ,
C=180°-A-B=90°
16
B
三角形中大边对大角
已知a=16, b= , A=30° .求角B,C和边c
例 2
所以
B=300,
或B=1500
由于1500 +450>1800
故B只有一解 (如图)
C=1050,
练习2: a=4, b= , A=45°求角B,C和边c
解:由正弦定理
得
450
A
B
C
4
三角形中大边对大角
A
B
C
α
β
地月距离如何测量呢?
构造三角形。
A
B
C
α
β
一个定理:正弦定理
两类应用
(1)已知两角及一边,解三角形
(2)已知两边及一边的对角,解三角形(要注意多解)
谈谈你这节课学到了什么?
三种思想
(1)从特殊到一般的思想方法
(2)分类讨论的思想
(3)化归思想
课堂小结:
必做题:1、课本P48第1、2 、3题
2、教辅P30例1、例2、例3
作业布置:
选做题:思考其他证明正弦定理的方法。
南宁市华侨实验高中 xx
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
