【解析版】山东省德州市2014届高三上学期1月月考 数学(理)试题
文档属性
| 名称 | 【解析版】山东省德州市2014届高三上学期1月月考 数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 560.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-07 15:52:14 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
山东德州市中学2014届高三1月月考数学理科
理科数学
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.21·世纪*教育网
1.若i为虚数单位,图1中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数的共轭复数是( ) www-2-1-cnjy-com
( http: / / www.21cnjy.com )
A.-i B.i C.-i D.i
( http: / / www.21cnjy.com )
2.已知 ( http: / / www.21cnjy.com )的最小值是 ( http: / / www.21cnjy.com ),则二项式 ( http: / / www.21cnjy.com )展开式中 ( http: / / www.21cnjy.com )项的系数为( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,有 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 单调递增,有 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .故函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的最小值为6,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,令 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,解得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,所以所求系数为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .故正确答案为A.2-1-c-n-j-y
考点:1.带有绝对值的函数的最值;2.二项式定理.
3.已知三个不等式:① HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;② HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;③ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ﹒要使同时满足①式和②的所有 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值都满足③式,则实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的取值范围是( )
A. B. C﹒ D﹒
( http: / / www.21cnjy.com )
4.已知二次函数 ( http: / / www.21cnjy.com )的导数 ( http: / / www.21cnjy.com ),且 ( http: / / www.21cnjy.com )的值域为 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的最小值为( )
A.3 B. ( http: / / www.21cnjy.com ) C.2 D. ( http: / / www.21cnjy.com )
【答案】C
( http: / / www.21cnjy.com )
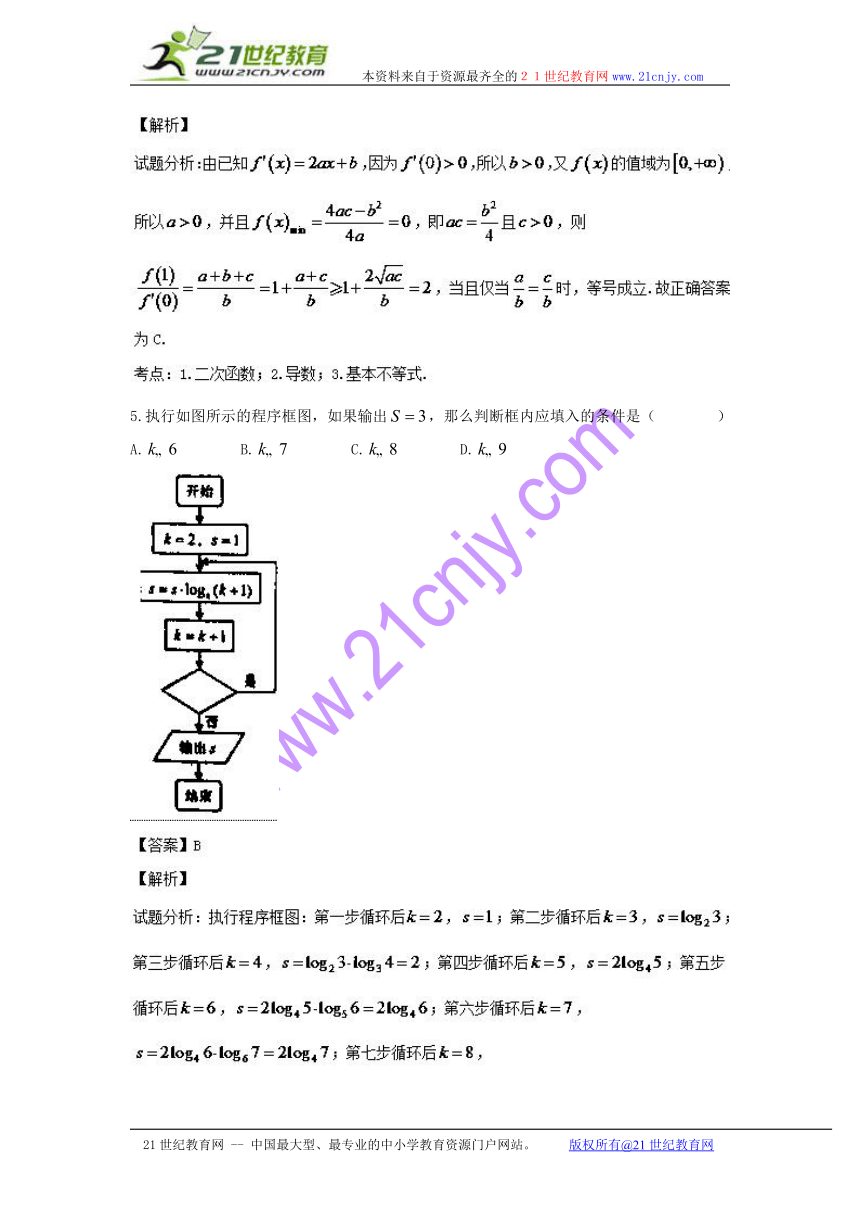
5.执行如图所示的程序框图,如果输出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,那么判断框内应填入的条件是( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .故正确答案为B.
考点:1.程序框图;2.对数运算.
6.六张卡片上分别写有数字1,1,2,3,4,5,从中取四张排成一排,可以组成不同的四位奇数的个数为( ) 21*cnjy*com
A.180 B.126 C.93 D.60
( http: / / www.21cnjy.com )
7.(2013.淄博一模)在区间 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 和 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 内分别取一个数,记为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 和 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则方程 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 表示离心率小于 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的双曲线的概率为( )【来源:21cnj*y.co*m】
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
( http: / / www.21cnjy.com )为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,由此可求出可行域范围内满足 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的面积为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,所以所求概率为 ( http: / / www.21cnjy.com )
8.将三颗骰子各掷一次,记事件A=“三个点数都不同”,B=“至少出现一个6点”,则条件概率 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 分别是( )【出处:21教育名师】
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
( http: / / www.21cnjy.com )
9.已知P(x,y)是直线 ( http: / / www.21cnjy.com )上一动点,PA,PB是圆C: ( http: / / www.21cnjy.com )的两条切线,A、B是切点,若四边形PACB的最小面积是2,则 ( http: / / www.21cnjy.com )的值为( )
A.3 B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.2
【答案】D
( http: / / www.21cnjy.com )
10.若直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 被圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 截得的弦长为4,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的最小值是( )
A.16 B.9 C.12 D.8
( http: / / www.21cnjy.com )
11.点P是双曲线 ( http: / / www.21cnjy.com )左支上的一点,其右焦点为 ( http: / / www.21cnjy.com ),若 ( http: / / www.21cnjy.com )为线段 ( http: / / www.21cnjy.com )的中点, 且 ( http: / / www.21cnjy.com )到坐标原点的距离为 ( http: / / www.21cnjy.com ),则双曲线的离心率 ( http: / / www.21cnjy.com )的取值范围是 ( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
12.已知椭圆 ( http: / / www.21cnjy.com )的左、右焦点分别为 ( http: / / www.21cnjy.com ),若椭圆上存在点P使 ( http: / / www.21cnjy.com ),则该椭圆的离心率的取值范围为( )
A.(0, ( http: / / www.21cnjy.com ) B.( ( http: / / www.21cnjy.com )) C.(0, ( http: / / www.21cnjy.com )) D.( ( http: / / www.21cnjy.com ),1)
( http: / / www.21cnjy.com )
第Ⅱ卷(共90分)
二、填空题(每题4分,满分16分,将答案填在答题纸上)
13.不等式 ( http: / / www.21cnjy.com )的解集为 .
( http: / / www.21cnjy.com )14.若不等式组 ( http: / / www.21cnjy.com )的解集中所含整数解只有-2,求 ( http: / / www.21cnjy.com )的取值范围 .
( http: / / www.21cnjy.com )
15.对大于或等于2的自然数 m的n 次方幂有如下分解方式:
22=1+3,32=1+3+5,42=1+3+5+7;23=3+5,33=7+9+11,43=13+15+17+19.
根据上述分解规律,若n2=1+3+5+…+19, m3(m∈N*)的分解中最小的数是21,则m+n的值为________.21世纪教育网版权所有
( http: / / www.21cnjy.com )
16.已知 ( http: / / www.21cnjy.com )满足约束条件 ( http: / / www.21cnjy.com ),则目标函数 ( http: / / www.21cnjy.com )的最大值是_______.
【答案】 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
【解析】
( http: / / www.21cnjy.com )
三、解答题 (本大题共6小题,17-21题各12分,22题14分,共74分﹒解答应写出文字说明、证明过程或演算步骤.) 21教育网
17.已知全集U=R,非空集合 ( http: / / www.21cnjy.com )< ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )< ( http: / / www.21cnjy.com ).
(1)当 ( http: / / www.21cnjy.com )时,求 ( http: / / www.21cnjy.com );
(2)命题 ( http: / / www.21cnjy.com ),命题 ( http: / / www.21cnjy.com ),若q是p的必要条件,求实数a的取值范围.
【答案】(1) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;(2) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 或 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
【解析】
试题分析:(1)由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,得 ( http: / / www.21cnjy.com )
18.设 ( http: / / www.21cnjy.com )
(1)当 ( http: / / www.21cnjy.com ),解不等式 ( http: / / www.21cnjy.com );
(2)当 ( http: / / www.21cnjy.com )时,若 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ),使得不等式 ( http: / / www.21cnjy.com )成立,求 ( http: / / www.21cnjy.com )的取值范围.
【答案】(1) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;(2) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ﹒
【解析】
试题分析:(1)当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,不等式 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,故所求不等式的解为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
( http: / / www.21cnjy.com )
19.为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
喜爱打篮球 不喜爱打篮球 合计
男生 5
女生 10
合计 50
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 ( http: / / www.21cnjy.com ).
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为ξ,求ξ的分布列与期望.
下面的临界值表供参考:
P(K2≥k) 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 2.072 2.706 3.841 5.024 6.635 7.879 10.828
(参考公式:K2= ( http: / / www.21cnjy.com ),其中n=a+b+c+d) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )分布列求出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的期望 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
试题解析:(1)列联表补充如下:﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)
喜爱打篮球 不喜爱打篮球 合计
男生 20 5 25
女生 10 15 25
合计 30 20 50
(2)∵K2= ( http: / / www.21cnjy.com )≈8.333>7.879﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)
∴在犯错误的概率不超过0.005的前提下,认为喜爱打篮球与性别有关.﹣﹣﹣﹣(6分)
( http: / / www.21cnjy.com )ξ的期望值为:Eξ=0 ( http: / / www.21cnjy.com )+1 ( http: / / www.21cnjy.com )+2 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)
考点:1.案例统计;2.古典概型.
20.从装有大小相同的2个红球和6个白球的袋子中,每摸出2个球为一次试验,直到摸出的球中有红球(不放回),则试验结束.21cnjy.com
(1)求第一次试验恰摸到一个红球和一个白球概率;
(2)记试验次数为 ( http: / / www.21cnjy.com ),求 ( http: / / www.21cnjy.com )的分布列及数学期望 ( http: / / www.21cnjy.com ).
【答案】(1) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;(2) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的分布列为
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 1 2 3 4
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
21.已知椭圆 ( http: / / www.21cnjy.com ),椭圆 ( http: / / www.21cnjy.com )以 ( http: / / www.21cnjy.com )的长轴为短轴,且与 ( http: / / www.21cnjy.com )有相同的离心率.
(1)求椭圆 ( http: / / www.21cnjy.com )的方程;
(2)设O为坐标原点,点A,B分别在椭圆 ( http: / / www.21cnjy.com )和 ( http: / / www.21cnjy.com )上, ( http: / / www.21cnjy.com ),求直线 ( http: / / www.21cnjy.com )的方程.
【答案】(1) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;(2) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 或 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
【解析】
试题分析:(1)由题意可设,所求椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,且其离心率可由椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的方程知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,因此 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,解之得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,从而可求出椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .21·cn·jy·com
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
22.如图,已知抛物线 ( http: / / www.21cnjy.com ): ( http: / / www.21cnjy.com )和⊙ ( http: / / www.21cnjy.com ): ( http: / / www.21cnjy.com ),过抛物线 ( http: / / www.21cnjy.com )上一点 ( http: / / www.21cnjy.com )作两条直线与⊙ ( http: / / www.21cnjy.com )相切于 ( http: / / www.21cnjy.com )、 ( http: / / www.21cnjy.com )两点,分别交抛物线为E、F两点,圆心点 ( http: / / www.21cnjy.com )到抛物线准线的距离为 ( http: / / www.21cnjy.com ).www.21-cn-jy.com
(1)求抛物线 ( http: / / www.21cnjy.com )的方程;
(2)当 ( http: / / www.21cnjy.com )的角平分线垂直 ( http: / / www.21cnjy.com )轴时,求直线 ( http: / / www.21cnjy.com )的斜率;
(3)若直线 ( http: / / www.21cnjy.com )在 ( http: / / www.21cnjy.com )轴上的截距为 ( http: / / www.21cnjy.com ),求 ( http: / / www.21cnjy.com )的最小值.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(2)由题意可知,直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 轴,可求出点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的坐标为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,此时直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的 ( http: / / www.21cnjy.com )(3)由题意可设点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的坐标分别为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,因为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的切线,所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,因此 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,由点斜式可求出直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的直线方程分别为 ( http: / / www.21cnjy.com )、 ( http: / / www.21cnjy.com ),又点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在抛物线上,有 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,所以点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的坐标为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,代入直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的方程得 ( http: / / www.21cnjy.com )、 ( http: / / www.21cnjy.com ),可整理为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,从而可求得直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,令 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,得直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上的截距为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,考虑到函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为单调递增函数,所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .2·1·c·n·j·y
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ). ( http: / / www.21cnjy.com ).-------------------7分
( http: / / www.21cnjy.com )∵ ( http: / / www.21cnjy.com )关于 ( http: / / www.21cnjy.com )的函数在 ( http: / / www.21cnjy.com )单调递增, ∴ ( http: / / www.21cnjy.com ).------------------------------14分【来源:21·世纪·教育·网】
法二:设点 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ).
以 ( http: / / www.21cnjy.com )为圆心, ( http: / / www.21cnjy.com )为半径的圆方程为 ( http: / / www.21cnjy.com ), ①
⊙ ( http: / / www.21cnjy.com )方程: ( http: / / www.21cnjy.com ). ②
①-②得:
直线 ( http: / / www.21cnjy.com )的方程为 ( http: / / www.21cnjy.com ).
当 ( http: / / www.21cnjy.com )时,直线 ( http: / / www.21cnjy.com )在 ( http: / / www.21cnjy.com )轴上的截距 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ),
∵ ( http: / / www.21cnjy.com )关于 ( http: / / www.21cnjy.com )的函数在 ( http: / / www.21cnjy.com )单调递增, ∴ ( http: / / www.21cnjy.com ). ------------------------14分
考点:1.抛物线方程;2.圆的方程;3.直线方程.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
山东德州市中学2014届高三1月月考数学理科
理科数学
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.21·世纪*教育网
1.若i为虚数单位,图1中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数的共轭复数是( ) www-2-1-cnjy-com
( http: / / www.21cnjy.com )
A.-i B.i C.-i D.i
( http: / / www.21cnjy.com )
2.已知 ( http: / / www.21cnjy.com )的最小值是 ( http: / / www.21cnjy.com ),则二项式 ( http: / / www.21cnjy.com )展开式中 ( http: / / www.21cnjy.com )项的系数为( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,有 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 单调递增,有 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .故函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的最小值为6,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,令 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,解得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,所以所求系数为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .故正确答案为A.2-1-c-n-j-y
考点:1.带有绝对值的函数的最值;2.二项式定理.
3.已知三个不等式:① HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;② HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;③ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ﹒要使同时满足①式和②的所有 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值都满足③式,则实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的取值范围是( )
A. B. C﹒ D﹒
( http: / / www.21cnjy.com )
4.已知二次函数 ( http: / / www.21cnjy.com )的导数 ( http: / / www.21cnjy.com ),且 ( http: / / www.21cnjy.com )的值域为 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的最小值为( )
A.3 B. ( http: / / www.21cnjy.com ) C.2 D. ( http: / / www.21cnjy.com )
【答案】C
( http: / / www.21cnjy.com )
5.执行如图所示的程序框图,如果输出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,那么判断框内应填入的条件是( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .故正确答案为B.
考点:1.程序框图;2.对数运算.
6.六张卡片上分别写有数字1,1,2,3,4,5,从中取四张排成一排,可以组成不同的四位奇数的个数为( ) 21*cnjy*com
A.180 B.126 C.93 D.60
( http: / / www.21cnjy.com )
7.(2013.淄博一模)在区间 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 和 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 内分别取一个数,记为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 和 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则方程 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 表示离心率小于 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的双曲线的概率为( )【来源:21cnj*y.co*m】
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
( http: / / www.21cnjy.com )为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,由此可求出可行域范围内满足 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的面积为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,所以所求概率为 ( http: / / www.21cnjy.com )
8.将三颗骰子各掷一次,记事件A=“三个点数都不同”,B=“至少出现一个6点”,则条件概率 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 分别是( )【出处:21教育名师】
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
( http: / / www.21cnjy.com )
9.已知P(x,y)是直线 ( http: / / www.21cnjy.com )上一动点,PA,PB是圆C: ( http: / / www.21cnjy.com )的两条切线,A、B是切点,若四边形PACB的最小面积是2,则 ( http: / / www.21cnjy.com )的值为( )
A.3 B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.2
【答案】D
( http: / / www.21cnjy.com )
10.若直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 被圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 截得的弦长为4,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的最小值是( )
A.16 B.9 C.12 D.8
( http: / / www.21cnjy.com )
11.点P是双曲线 ( http: / / www.21cnjy.com )左支上的一点,其右焦点为 ( http: / / www.21cnjy.com ),若 ( http: / / www.21cnjy.com )为线段 ( http: / / www.21cnjy.com )的中点, 且 ( http: / / www.21cnjy.com )到坐标原点的距离为 ( http: / / www.21cnjy.com ),则双曲线的离心率 ( http: / / www.21cnjy.com )的取值范围是 ( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
12.已知椭圆 ( http: / / www.21cnjy.com )的左、右焦点分别为 ( http: / / www.21cnjy.com ),若椭圆上存在点P使 ( http: / / www.21cnjy.com ),则该椭圆的离心率的取值范围为( )
A.(0, ( http: / / www.21cnjy.com ) B.( ( http: / / www.21cnjy.com )) C.(0, ( http: / / www.21cnjy.com )) D.( ( http: / / www.21cnjy.com ),1)
( http: / / www.21cnjy.com )
第Ⅱ卷(共90分)
二、填空题(每题4分,满分16分,将答案填在答题纸上)
13.不等式 ( http: / / www.21cnjy.com )的解集为 .
( http: / / www.21cnjy.com )14.若不等式组 ( http: / / www.21cnjy.com )的解集中所含整数解只有-2,求 ( http: / / www.21cnjy.com )的取值范围 .
( http: / / www.21cnjy.com )
15.对大于或等于2的自然数 m的n 次方幂有如下分解方式:
22=1+3,32=1+3+5,42=1+3+5+7;23=3+5,33=7+9+11,43=13+15+17+19.
根据上述分解规律,若n2=1+3+5+…+19, m3(m∈N*)的分解中最小的数是21,则m+n的值为________.21世纪教育网版权所有
( http: / / www.21cnjy.com )
16.已知 ( http: / / www.21cnjy.com )满足约束条件 ( http: / / www.21cnjy.com ),则目标函数 ( http: / / www.21cnjy.com )的最大值是_______.
【答案】 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
【解析】
( http: / / www.21cnjy.com )
三、解答题 (本大题共6小题,17-21题各12分,22题14分,共74分﹒解答应写出文字说明、证明过程或演算步骤.) 21教育网
17.已知全集U=R,非空集合 ( http: / / www.21cnjy.com )< ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )< ( http: / / www.21cnjy.com ).
(1)当 ( http: / / www.21cnjy.com )时,求 ( http: / / www.21cnjy.com );
(2)命题 ( http: / / www.21cnjy.com ),命题 ( http: / / www.21cnjy.com ),若q是p的必要条件,求实数a的取值范围.
【答案】(1) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;(2) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 或 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
【解析】
试题分析:(1)由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,得 ( http: / / www.21cnjy.com )
18.设 ( http: / / www.21cnjy.com )
(1)当 ( http: / / www.21cnjy.com ),解不等式 ( http: / / www.21cnjy.com );
(2)当 ( http: / / www.21cnjy.com )时,若 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ),使得不等式 ( http: / / www.21cnjy.com )成立,求 ( http: / / www.21cnjy.com )的取值范围.
【答案】(1) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;(2) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ﹒
【解析】
试题分析:(1)当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,不等式 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,故所求不等式的解为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
( http: / / www.21cnjy.com )
19.为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
喜爱打篮球 不喜爱打篮球 合计
男生 5
女生 10
合计 50
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 ( http: / / www.21cnjy.com ).
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为ξ,求ξ的分布列与期望.
下面的临界值表供参考:
P(K2≥k) 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 2.072 2.706 3.841 5.024 6.635 7.879 10.828
(参考公式:K2= ( http: / / www.21cnjy.com ),其中n=a+b+c+d) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )分布列求出 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的期望 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
试题解析:(1)列联表补充如下:﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)
喜爱打篮球 不喜爱打篮球 合计
男生 20 5 25
女生 10 15 25
合计 30 20 50
(2)∵K2= ( http: / / www.21cnjy.com )≈8.333>7.879﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)
∴在犯错误的概率不超过0.005的前提下,认为喜爱打篮球与性别有关.﹣﹣﹣﹣(6分)
( http: / / www.21cnjy.com )ξ的期望值为:Eξ=0 ( http: / / www.21cnjy.com )+1 ( http: / / www.21cnjy.com )+2 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)
考点:1.案例统计;2.古典概型.
20.从装有大小相同的2个红球和6个白球的袋子中,每摸出2个球为一次试验,直到摸出的球中有红球(不放回),则试验结束.21cnjy.com
(1)求第一次试验恰摸到一个红球和一个白球概率;
(2)记试验次数为 ( http: / / www.21cnjy.com ),求 ( http: / / www.21cnjy.com )的分布列及数学期望 ( http: / / www.21cnjy.com ).
【答案】(1) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;(2) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的分布列为
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 1 2 3 4
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
21.已知椭圆 ( http: / / www.21cnjy.com ),椭圆 ( http: / / www.21cnjy.com )以 ( http: / / www.21cnjy.com )的长轴为短轴,且与 ( http: / / www.21cnjy.com )有相同的离心率.
(1)求椭圆 ( http: / / www.21cnjy.com )的方程;
(2)设O为坐标原点,点A,B分别在椭圆 ( http: / / www.21cnjy.com )和 ( http: / / www.21cnjy.com )上, ( http: / / www.21cnjy.com ),求直线 ( http: / / www.21cnjy.com )的方程.
【答案】(1) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;(2) HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 或 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
【解析】
试题分析:(1)由题意可设,所求椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,且其离心率可由椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的方程知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,因此 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,解之得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,从而可求出椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .21·cn·jy·com
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
22.如图,已知抛物线 ( http: / / www.21cnjy.com ): ( http: / / www.21cnjy.com )和⊙ ( http: / / www.21cnjy.com ): ( http: / / www.21cnjy.com ),过抛物线 ( http: / / www.21cnjy.com )上一点 ( http: / / www.21cnjy.com )作两条直线与⊙ ( http: / / www.21cnjy.com )相切于 ( http: / / www.21cnjy.com )、 ( http: / / www.21cnjy.com )两点,分别交抛物线为E、F两点,圆心点 ( http: / / www.21cnjy.com )到抛物线准线的距离为 ( http: / / www.21cnjy.com ).www.21-cn-jy.com
(1)求抛物线 ( http: / / www.21cnjy.com )的方程;
(2)当 ( http: / / www.21cnjy.com )的角平分线垂直 ( http: / / www.21cnjy.com )轴时,求直线 ( http: / / www.21cnjy.com )的斜率;
(3)若直线 ( http: / / www.21cnjy.com )在 ( http: / / www.21cnjy.com )轴上的截距为 ( http: / / www.21cnjy.com ),求 ( http: / / www.21cnjy.com )的最小值.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(2)由题意可知,直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 轴,可求出点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的坐标为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,此时直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的 ( http: / / www.21cnjy.com )(3)由题意可设点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的坐标分别为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,因为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的切线,所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,因此 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,由点斜式可求出直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的直线方程分别为 ( http: / / www.21cnjy.com )、 ( http: / / www.21cnjy.com ),又点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在抛物线上,有 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,所以点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的坐标为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,代入直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的方程得 ( http: / / www.21cnjy.com )、 ( http: / / www.21cnjy.com ),可整理为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,从而可求得直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的方程为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,令 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,得直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上的截距为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,考虑到函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为单调递增函数,所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .2·1·c·n·j·y
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ). ( http: / / www.21cnjy.com ).-------------------7分
( http: / / www.21cnjy.com )∵ ( http: / / www.21cnjy.com )关于 ( http: / / www.21cnjy.com )的函数在 ( http: / / www.21cnjy.com )单调递增, ∴ ( http: / / www.21cnjy.com ).------------------------------14分【来源:21·世纪·教育·网】
法二:设点 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ).
以 ( http: / / www.21cnjy.com )为圆心, ( http: / / www.21cnjy.com )为半径的圆方程为 ( http: / / www.21cnjy.com ), ①
⊙ ( http: / / www.21cnjy.com )方程: ( http: / / www.21cnjy.com ). ②
①-②得:
直线 ( http: / / www.21cnjy.com )的方程为 ( http: / / www.21cnjy.com ).
当 ( http: / / www.21cnjy.com )时,直线 ( http: / / www.21cnjy.com )在 ( http: / / www.21cnjy.com )轴上的截距 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ),
∵ ( http: / / www.21cnjy.com )关于 ( http: / / www.21cnjy.com )的函数在 ( http: / / www.21cnjy.com )单调递增, ∴ ( http: / / www.21cnjy.com ). ------------------------14分
考点:1.抛物线方程;2.圆的方程;3.直线方程.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
