【解析版】山东省烟台市2014届高三上学期期末考试 数学文科试题
文档属性
| 名称 | 【解析版】山东省烟台市2014届高三上学期期末考试 数学文科试题 |  | |
| 格式 | zip | ||
| 文件大小 | 443.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-07 15:57:05 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
山东省烟台市2014届高三上学期期末考试
数学(文科)试卷
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.设全集,集合,,则 ( http: / / www.21cnjy.com )等于( )
A. B. C. D.
( http: / / www.21cnjy.com )
2.若,,,则( )
A. B.
C. D.
( http: / / www.21cnjy.com )
3.下列四个函数中,最小正周期为,且图象关于直线对称的是( )
A. B.
C. D.
【答案】D
【解析】
( http: / / www.21cnjy.com )
4.设平面向量,,若,则等于( )
A.4 B.5 C. D.
( http: / / www.21cnjy.com )
5.在ABC中,若,则A=( )
A. B. C. D.
( http: / / www.21cnjy.com )
6.函数的零点所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3.4)
【答案】B
试题分析:函数在区间存在零点,等价于.
计算,故选B.
考点:函数零点存在定理
7.已知直线l平面,直线平面,则下列四个结论:
①若,则 ②若,则
③若,则 ④若,则
其中正确的结论的序号是:( )
A.①④ B.②④ C.①③ D.②③
( http: / / www.21cnjy.com )
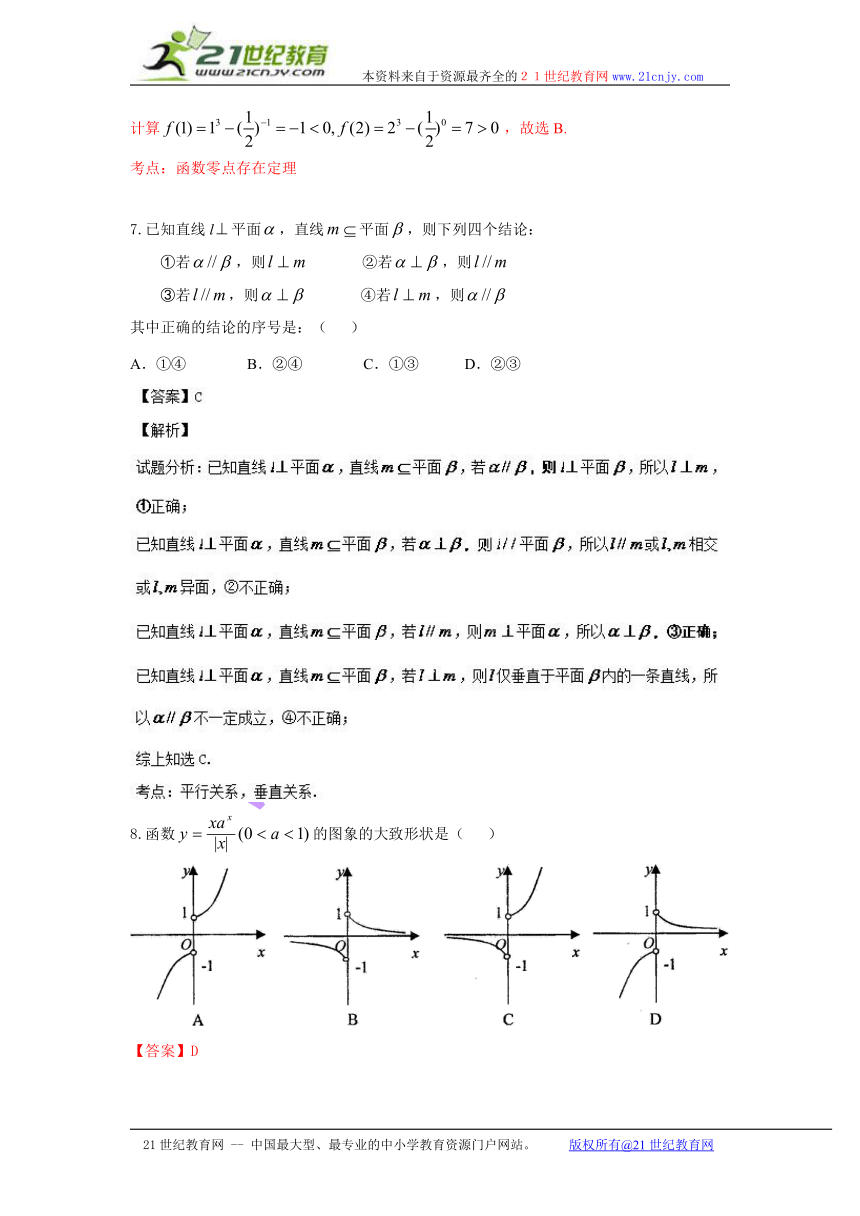
8.函数的图象的大致形状是( )
( http: / / www.21cnjy.com )
【答案】D
( http: / / www.21cnjy.com )
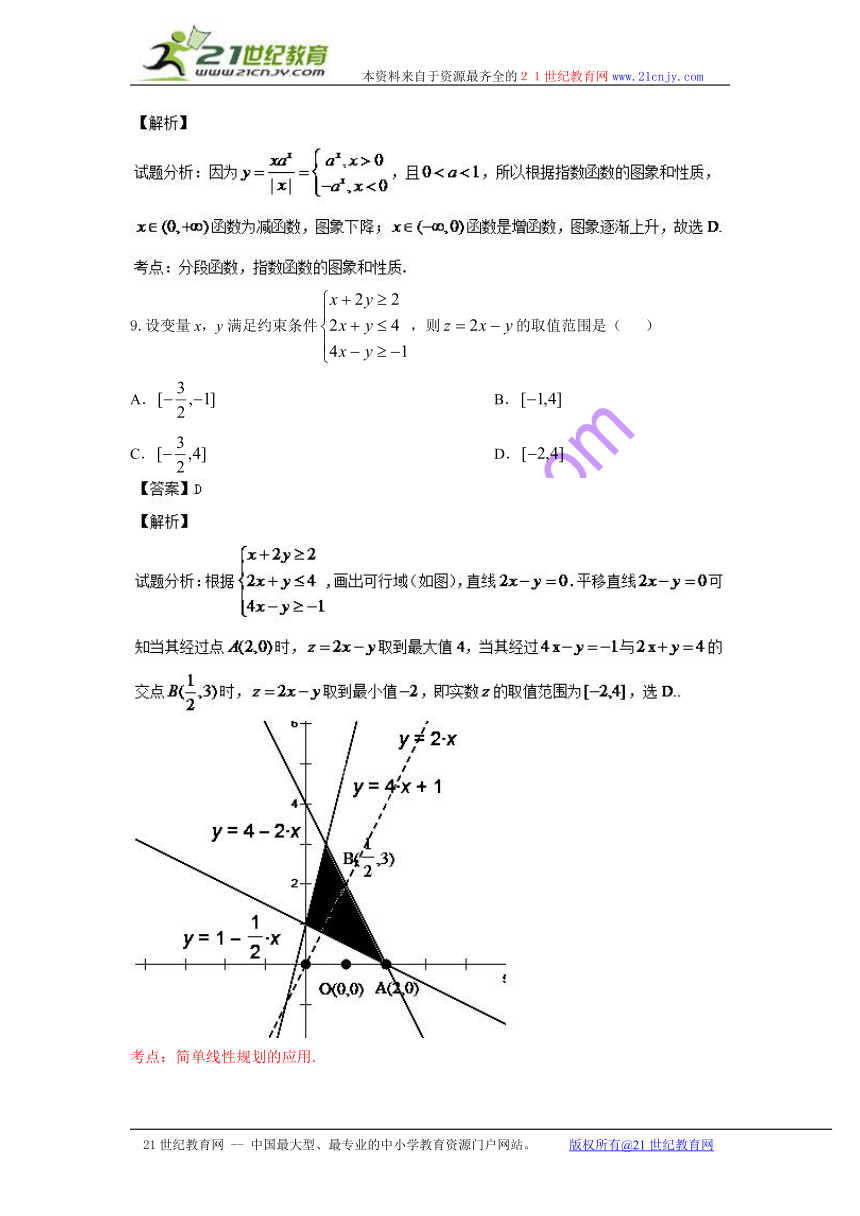
9.设变量x,y满足约束条件,则的取值范围是( )
A. B.
C. D.
( http: / / www.21cnjy.com )考点:简单线性规划的应用.
10.一个几何体的三视图如图所示,则这个几何体的体积为( )
( http: / / www.21cnjy.com )
A. B.9 C. D.27
( http: / / www.21cnjy.com )
11.若双曲线的渐近线与抛物线相切,则此双曲线的离心率等于( )
A.2 B.3 C. D.9
( http: / / www.21cnjy.com )考点:双曲线的几何性质,直线与抛物线的位置关系.
12.已知函数满足,且是偶函数,当时,,若在区间内,函数有三个零点,则实数k的取值范围是( )
A. B. C. D.
( http: / / www.21cnjy.com )
第Ⅱ卷(共90分)
二、填空题(每题4分,满分16分,将答案填在答题纸上)
13.函数的定义域为______________.
( http: / / www.21cnjy.com )14.若直线与x轴相交于点A,与y轴相交于点B,且以坐标原点为圆心以为半径的圆与直线l相切,则△AOB面积为_____________.21世纪教育网版权所有
( http: / / www.21cnjy.com )
15.设等差数列的前n项和为Sn,,则正整数m的值为_____________.
【答案】5
【解析】
试题分析:因为等差数列的前n项和为Sn,,
所以,数列的公差.
由,得正整数m的值为5.
考点:等差数列的求和公式
16.给出以下四个结论:
①函数的对称中心是
②若不等式对任意的x∈R都成立,则;
③已知点与点Q(l,0)在直线两侧,则;
④若将函数的图像向右平移个单位后变为偶函数,则的最小值是.
其中正确的结论是____________(写出所有正确结论的编号).
( http: / / www.21cnjy.com )
三、解答题 (本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分12分)
在平面直角坐标系中,角α,β的始边为x轴的非负半轴,点在角α的终边上,点在角β的终边上,且
(1)求
(2)求P,Q的坐标并求的值
( http: / / www.21cnjy.com )(2)由(1)得:, ∴
, ∴ ……………7分
∴ ,, ……………9分
∴ ,,
,, ……………11分
……………12分
考点:任意角的三角函数,和差倍半的三角函数.
18.(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,,,DC=1,AB=2,PA⊥平面ABCD,PA =1.21教育网
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
19.(本小题满分12分)
已知数列的前n项和为,
(1)求证:数列为等差数列;
(2)设数列的前n项和为Tn,求Tn.
( http: / / www.21cnjy.com ) …………6分
(2)由(1)得:,
, ………9分
, …………12分
考点:等差数列的概念,“裂项相消法”.
20.(本小题满分l2分)
近日,国家经贸委发出了关于深入开展增产节约运动,大力增产市场适销对路产品的通知,并发布了当前国内市场185种适销工业品和42种滞销产品的参考目录。为此,一公司举行某产品的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用x万元满足(其中,a为正常数);已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为万元/万件.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润是大?
( http: / / www.21cnjy.com )(2),
当且仅当时,上式取等号. ……………………9分
当时, 促销费用投入1万元时,厂家的利润最大;
当时, 在上单调递增,所以在时,函数有最大值.促销费用投入万元时,厂家的利润最大 .
综上述,当时, 促销费用投入1万元时,厂家的利润最大;
当时,促销费用投入万元时,厂家的利润最大 . ……………………12分
考点:函数的应用问题,基本不等式.
21.(本小题满分13分)
已知是二次函数,不等式的解集是,且在点处的切线与直线平行.
(1)求的解析式;
(2)是否存在t∈N*,使得方程在区间内有两个不等的实数根?
若存在,求出t的值;若不存在,说明理由.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
当时,,函数在上单调递增. … 9分
∵,
( http: / / www.21cnjy.com )
22.(本小题满分13分)
已知椭圆的左、右焦点分别为,且,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
(1)求椭圆方程;
(2)设椭圆与直线相交于不同的两点M、N,又点,当时,求实数m的取值范围,
( http: / / www.21cnjy.com )(2)当时,直线和椭圆有两交点只需; ………………5分
( http: / / www.21cnjy.com )
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
山东省烟台市2014届高三上学期期末考试
数学(文科)试卷
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.设全集,集合,,则 ( http: / / www.21cnjy.com )等于( )
A. B. C. D.
( http: / / www.21cnjy.com )
2.若,,,则( )
A. B.
C. D.
( http: / / www.21cnjy.com )
3.下列四个函数中,最小正周期为,且图象关于直线对称的是( )
A. B.
C. D.
【答案】D
【解析】
( http: / / www.21cnjy.com )
4.设平面向量,,若,则等于( )
A.4 B.5 C. D.
( http: / / www.21cnjy.com )
5.在ABC中,若,则A=( )
A. B. C. D.
( http: / / www.21cnjy.com )
6.函数的零点所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3.4)
【答案】B
试题分析:函数在区间存在零点,等价于.
计算,故选B.
考点:函数零点存在定理
7.已知直线l平面,直线平面,则下列四个结论:
①若,则 ②若,则
③若,则 ④若,则
其中正确的结论的序号是:( )
A.①④ B.②④ C.①③ D.②③
( http: / / www.21cnjy.com )
8.函数的图象的大致形状是( )
( http: / / www.21cnjy.com )
【答案】D
( http: / / www.21cnjy.com )
9.设变量x,y满足约束条件,则的取值范围是( )
A. B.
C. D.
( http: / / www.21cnjy.com )考点:简单线性规划的应用.
10.一个几何体的三视图如图所示,则这个几何体的体积为( )
( http: / / www.21cnjy.com )
A. B.9 C. D.27
( http: / / www.21cnjy.com )
11.若双曲线的渐近线与抛物线相切,则此双曲线的离心率等于( )
A.2 B.3 C. D.9
( http: / / www.21cnjy.com )考点:双曲线的几何性质,直线与抛物线的位置关系.
12.已知函数满足,且是偶函数,当时,,若在区间内,函数有三个零点,则实数k的取值范围是( )
A. B. C. D.
( http: / / www.21cnjy.com )
第Ⅱ卷(共90分)
二、填空题(每题4分,满分16分,将答案填在答题纸上)
13.函数的定义域为______________.
( http: / / www.21cnjy.com )14.若直线与x轴相交于点A,与y轴相交于点B,且以坐标原点为圆心以为半径的圆与直线l相切,则△AOB面积为_____________.21世纪教育网版权所有
( http: / / www.21cnjy.com )
15.设等差数列的前n项和为Sn,,则正整数m的值为_____________.
【答案】5
【解析】
试题分析:因为等差数列的前n项和为Sn,,
所以,数列的公差.
由,得正整数m的值为5.
考点:等差数列的求和公式
16.给出以下四个结论:
①函数的对称中心是
②若不等式对任意的x∈R都成立,则;
③已知点与点Q(l,0)在直线两侧,则;
④若将函数的图像向右平移个单位后变为偶函数,则的最小值是.
其中正确的结论是____________(写出所有正确结论的编号).
( http: / / www.21cnjy.com )
三、解答题 (本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分12分)
在平面直角坐标系中,角α,β的始边为x轴的非负半轴,点在角α的终边上,点在角β的终边上,且
(1)求
(2)求P,Q的坐标并求的值
( http: / / www.21cnjy.com )(2)由(1)得:, ∴
, ∴ ……………7分
∴ ,, ……………9分
∴ ,,
,, ……………11分
……………12分
考点:任意角的三角函数,和差倍半的三角函数.
18.(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,,,DC=1,AB=2,PA⊥平面ABCD,PA =1.21教育网
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
19.(本小题满分12分)
已知数列的前n项和为,
(1)求证:数列为等差数列;
(2)设数列的前n项和为Tn,求Tn.
( http: / / www.21cnjy.com ) …………6分
(2)由(1)得:,
, ………9分
, …………12分
考点:等差数列的概念,“裂项相消法”.
20.(本小题满分l2分)
近日,国家经贸委发出了关于深入开展增产节约运动,大力增产市场适销对路产品的通知,并发布了当前国内市场185种适销工业品和42种滞销产品的参考目录。为此,一公司举行某产品的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用x万元满足(其中,a为正常数);已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为万元/万件.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润是大?
( http: / / www.21cnjy.com )(2),
当且仅当时,上式取等号. ……………………9分
当时, 促销费用投入1万元时,厂家的利润最大;
当时, 在上单调递增,所以在时,函数有最大值.促销费用投入万元时,厂家的利润最大 .
综上述,当时, 促销费用投入1万元时,厂家的利润最大;
当时,促销费用投入万元时,厂家的利润最大 . ……………………12分
考点:函数的应用问题,基本不等式.
21.(本小题满分13分)
已知是二次函数,不等式的解集是,且在点处的切线与直线平行.
(1)求的解析式;
(2)是否存在t∈N*,使得方程在区间内有两个不等的实数根?
若存在,求出t的值;若不存在,说明理由.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
当时,,函数在上单调递增. … 9分
∵,
( http: / / www.21cnjy.com )
22.(本小题满分13分)
已知椭圆的左、右焦点分别为,且,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
(1)求椭圆方程;
(2)设椭圆与直线相交于不同的两点M、N,又点,当时,求实数m的取值范围,
( http: / / www.21cnjy.com )(2)当时,直线和椭圆有两交点只需; ………………5分
( http: / / www.21cnjy.com )
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
