3.6三角形内角和定理1

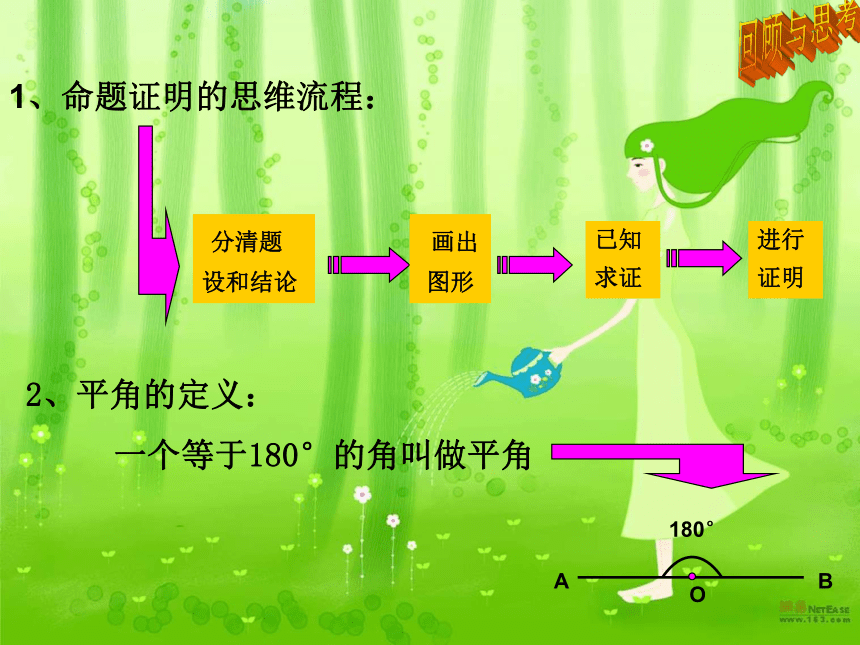
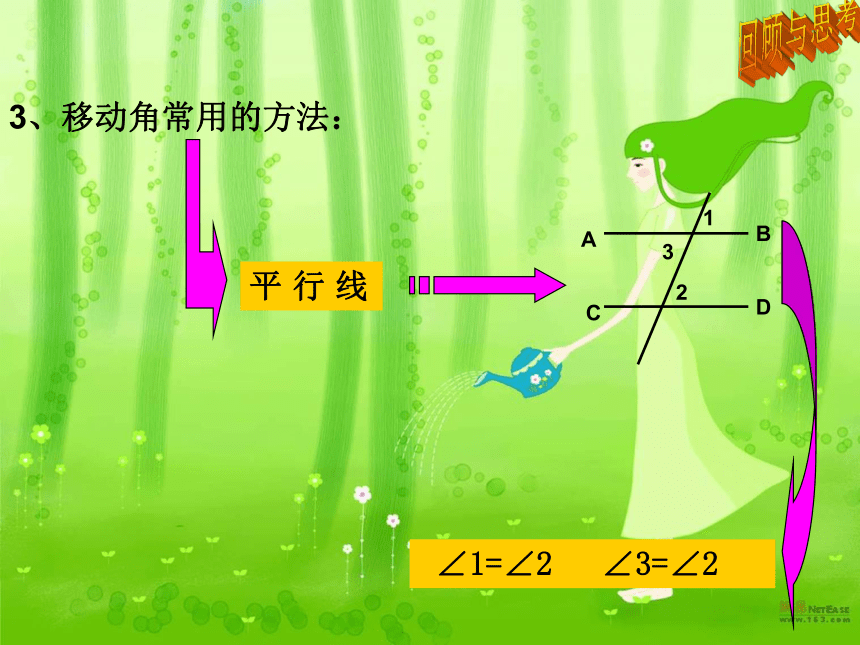
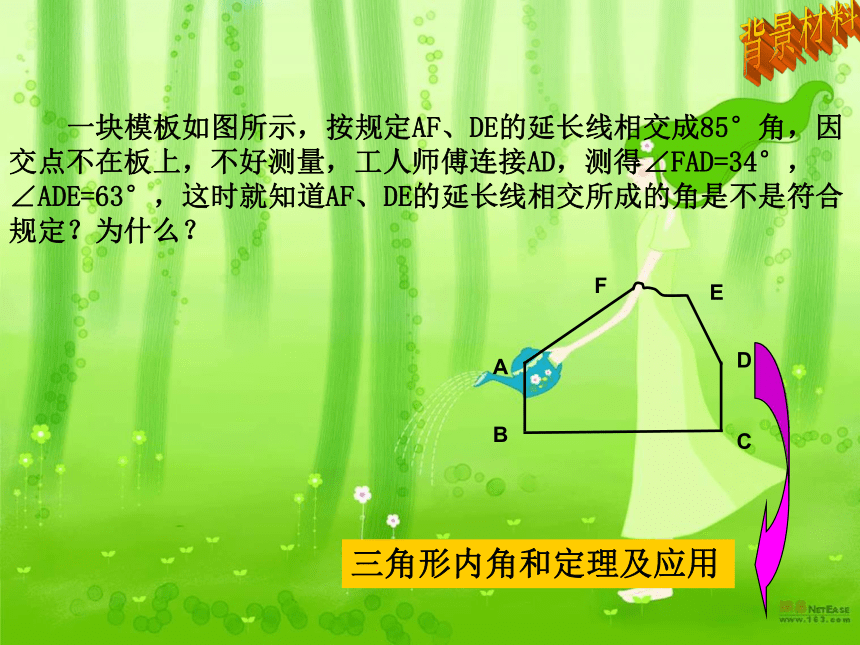
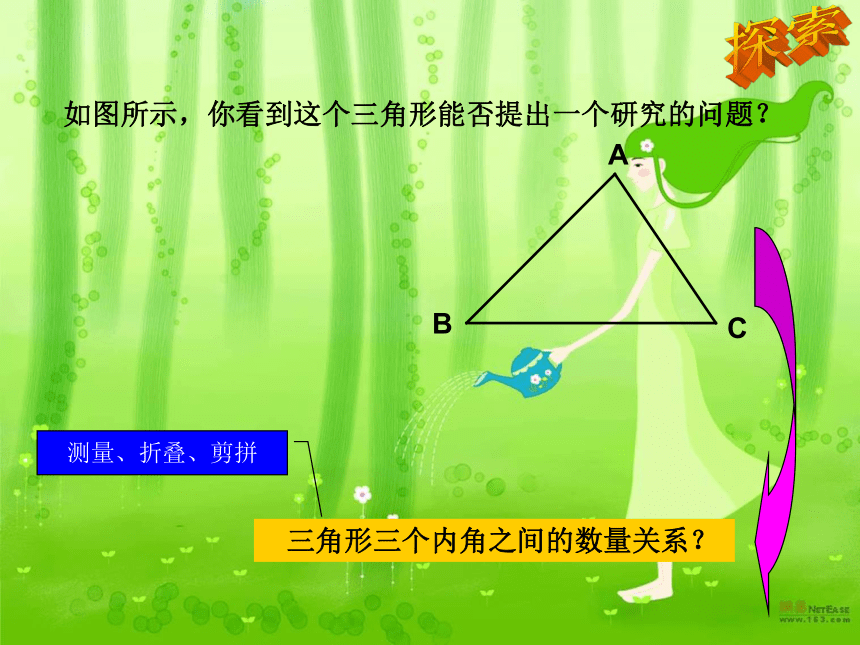
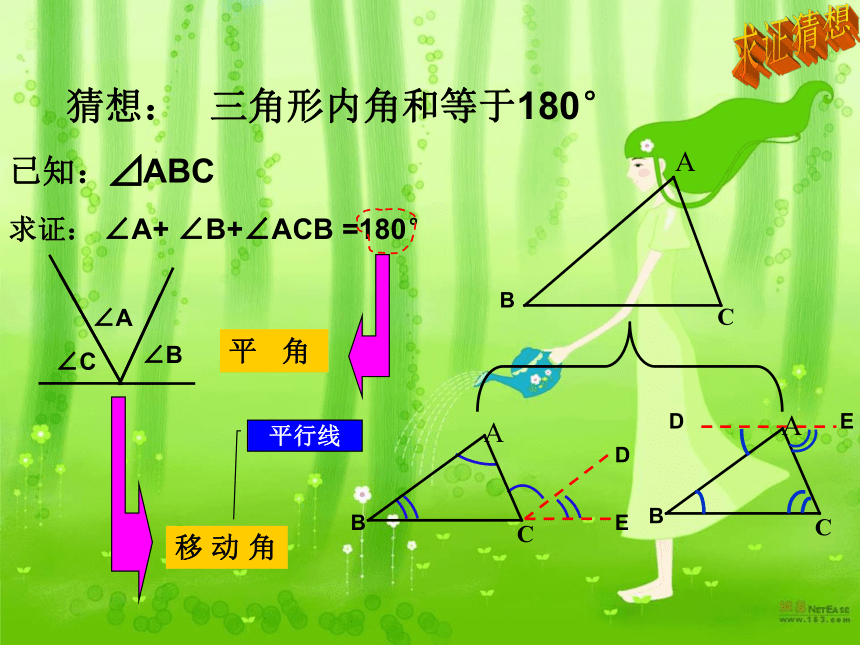
课件21张PPT。 义务教育课程标准实验教科书 数学 八年级上册 QQ:315743419三角形内角和定理（一）1、命题证明的思维流程： 分清题设和结论 画出 图形 已知求证 进行证明 2、平角的定义：一个等于180°的角叫做平角180°回顾与思考3、移动角常用的方法：1平 行 线23 ∠1=∠2回顾与思考∠3=∠2 一块模板如图所示，按规定AF、DE的延长线相交成85°角，因交点不在板上，不好测量，工人师傅连接AD，测得∠FAD=34°，∠ADE=63°，这时就知道AF、DE的延长线相交所成的角是不是符合规定？为什么？三角形内角和定理及应用背景材料 三角形内角和定理及应用知识梳理 如图所示，你看到这个三角形能否提出一个研究的问题？ 三角形三个内角之间的数量关系？探索测量、折叠、剪拼 三角形内角和等于180°发现 三角形内角和等于180°猜想：已知：⊿ABC求证： ∠A+ ∠B+∠ACB =180°平 角移 动 角DEDE求证猜想平行线 三角形内角和等于180°猜想：已知：⊿ABC求证： ∠A+ ∠B+∠ACB =180°DE证明：过点C作CD∥AB，延长BC到E∵ CD∥AB∴ ∠ACD=∠A∠DCE=∠B∴∠A+∠B+ ∠ACB= ∠ACB+ ∠ACD+∠DCE =180°求证猜想 三角形内角和定理及应用 一、 三角形内角和定理：∵⊿ABC∵∠A+ ∠B+ ∠C=180° 三角形内角和等于180°知识梳理A组 如图所示，AC、BD 相交于点O，
如果∠A+ ∠B=m, ∠C+ ∠D=n则 m和n的大小关系是________B组 在⊿ABC中,∠A:∠B:∠C =1:2:3则⊿ABC的形状_____m= ?n= ?180°- ∠AOB180°- ∠AOB方程思想直角三角形 x=30°m=n试一试 x+2x+3x=180°设∠A=x ∠B=2x ∠C=3x 三角形内角和定理及应用 一、 三角形内角和定理：∵⊿ABC∴∠A+ ∠B+ ∠C=180° 三角形内角和等于180°知识梳理二、 应用:求： ∠BDE +∠DEC 的度数 例1 如图所示，在⊿ABC中，∠A=80°∠BDE +∠DEC80°探究1∠BDE=180°- ∠ADE∠DEC=180°- ∠AED∠BDE+ ∠DEC=360°-（∠ADE+ ∠AED) ∠ADE+ ∠AED=100°∠BDE+ ∠DEC=260°求：∠BDE +∠DEC 的度数 例1 如图所示，在⊿ABC中，∠A=80°解： ∵∠BDE = 180°- ∠ADE∠DEC = 180°- ∠AED∴∠BDE +∠DEC = （180°- ∠ADE）+ （180°- ∠AED） = 360°- (∠ADE+ ∠ AED)探究180°∵ ∠ADE+ ∠ AED = 180°- 80°= 100°∴∠BDE +∠DEC = 360°- 100° = 260°∠ADE+ ∠AED=100°例2 如图所示， 求：∠A+ ∠B+ ∠C+ ∠D+ ∠ E的度数∠A+ ∠ABE+ ∠ ACD +∠EBC+ ∠BCD探究2∠D+ ∠E = ∠EBC+ ∠BCD ⊿ABC的内角和例2 如图所示， 求：∠A+ ∠B+ ∠C+ ∠D+ ∠ E的度数探究2∠D+ ∠E = ∠EBC+ ∠BCD ∵∠D+∠E=∠EBC+ ∠BCD解：连接BC∴ ∠A+ ∠ABE+ ∠ACD+ ∠D+ ∠E= ∠A+ ∠ABE+ ∠ACD+ ∠EBC+ ∠BCD= 180°⊿ABC的内角和 三角形内角和定理及应用一、 三角形内角和定理：∵⊿ABC∴∠A+ ∠B+ ∠C=180° 三角形内角和等于180°知识梳理二、 应用:把不规则图形角的和问题化归为三角形内角和问题
连接相邻两点
基本图形则∠A+ ∠B+ ∠B +∠D+ ∠E= ____180°我能行构造出⊿AEC⊿AEC的内角和？ 一块模板如图所示，按规定AF、DE的延长线相交成85°角，因交点不在板上，不好测量。工人师傅连接AD，测得∠FAD=34°，∠ADE=63°，这时就知道AF、DE的延长线相交所成的角是不是符合规定？为什么？∠G与85°的数量关系34°63°G∠G=180°-∠FAD-∠EDA=180°-34°-63°=83°∠G=？背景材料∠G放到⊿ADG 一块模板如图所示，按规定AF、DE的延长线相交成85°角，因交点不在板上，不测量，工人师傅连接AD，测得∠FAD=34°，∠ADE=63°，这时就知道AF、DE的延长线相交所成的角是不是符合规定？为什么？34°63°G∵∠G≠85°解：∵∠FAD=34°∠EAD=34°∴ ∠G=180°-34°-63° =83°∴该模板不合格延长AF、DE相交于点G，连接AD背景材料