18.2.1平行四边形的判定(1) 课件
文档属性
| 名称 | 18.2.1平行四边形的判定(1) 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
18.2.1平行四边形的判定(1)
华师大版 八年级 下册
教学目标
教学目标:1.理解并掌握“平行四边形的定义判定一个四边形是平行四
边形”.
2.理解并掌握“两组对边分别相等的四边形是平行四边形”.
3.理解并掌握“一组对边平行且相等的四边形是平行四边形”.
教学重点:平行四边形的判定方法及应用.
教学难点:平行四边形的判定定理的灵活应用.
新知导入
情境引入
一装潢店要招聘店员,老板出了这样一道考题:“一顾客要一张平行四边形的玻璃,你利用工具度量哪些数据可说明这张玻璃符合顾客要求.”
你能帮助他回答这个问题吗?
度量哪些数据?
两组对边的长度是否相等.
能说出理由吗?
新知讲解
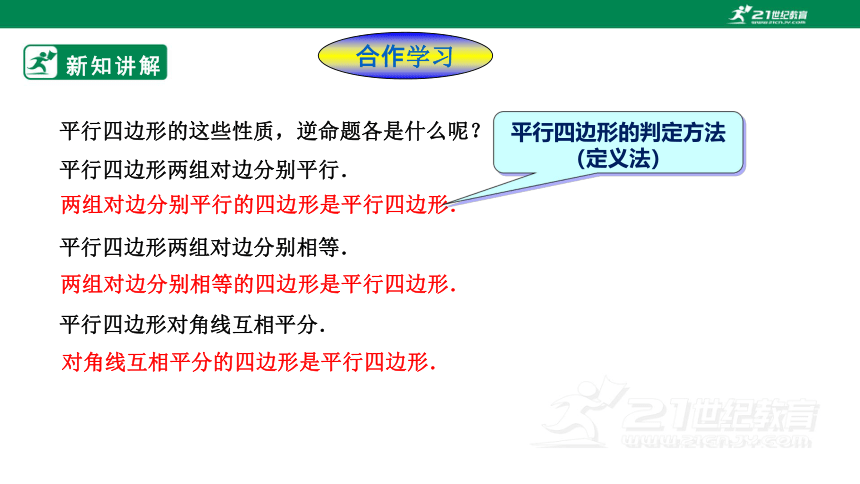
合作学行四边形的这些性质,逆命题各是什么呢?
平行四边形两组对边分别平行.
平行四边形两组对边分别相等.
平行四边形对角线互相平分.
两组对边分别相等的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
平行四边形的判定方法(定义法)
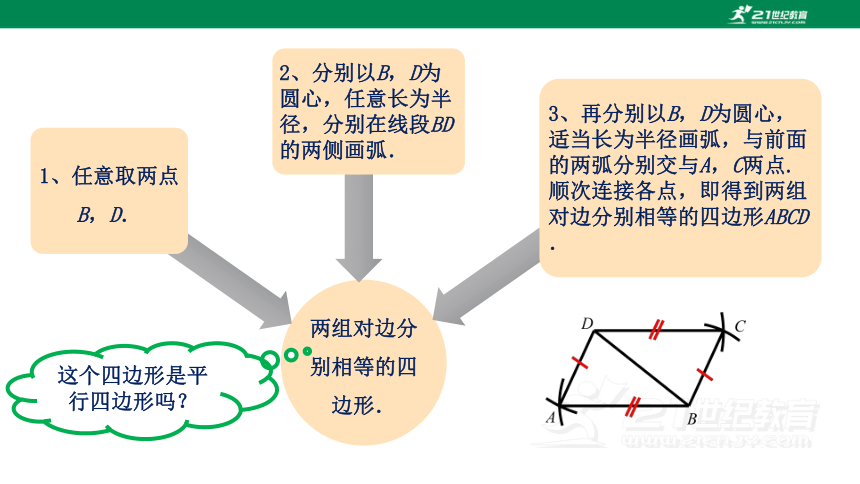
两组对边分别相等的四边形.
1、任意取两点B,D.
2、分别以B,D为圆心,任意长为半径,分别在线段BD的两侧画弧.
3、再分别以B,D为圆心,适当长为半径画弧,与前面的两弧分别交与A,C两点.顺次连接各点,即得到两组对边分别相等的四边形ABCD.
这个四边形是平行四边形吗?
凭直觉和测量都确实感受到它是平行四边形我们如何用推理的方法加以证明呢?试一试吧!也许会成功
已知:在四边形ABCD中, AB=CD , AD=BC
求证:四边形ABCD 是平行四边形
证明思路
AB//CD, AD //BC
∠1=∠2,∠3=∠4
⊿ABC≌⊿CDA
两组对边分别相等的四边形是平行四边形.
已知:如图,在四边形ABCD中,AB=DC,AD=BC.
求证:四边形ABCD是平行四边形 .
证明:连结AC.
∵AD=BC,AB=DC,AC=AC,
∴△ABC≌ △ CDA(SSS),
∴∠1= ∠2,∠3=∠4 (全等三角形的性质).
∴AB∥CD,AD∥BC(内错角相等,两直线平行).
∴四边形ABCD是平行四边形.(两组对边分别平行的四边形是平行四边形)
平行四边形的判定方法1
两组对边分别相等的四边形是平行四边形.
平行四边形的判定定理1:
符号语言:
∵AB=CD,AD=BC.
∴四边形ABCD是平行四边形.
(两组对边分别相等的四边形是平行四边形)
如果知道了一组对边相等,那么再加上一个什么条件也可以得到一个平行四边形?
一组对边平行且相等的四边形是平行四边形.
一组对边平行,另一组对边相等的四边形是平行四边形.
一组对边平行且相等的四边形.
1、任意画两条平行线m,n.
2、在直线m,n上分别截取AB、CD,使AB、CD .
3、分别连结点B,C和点A,D.
这个四边形是平行四边形吗?
已知:如图、在四边形ABCD中,AB∥CD、AB=CD
求证:四边形ABCD是平行四边形
证明思路
AB∥CD, AD ∥BC
∠1=∠2,∠3=∠4
⊿ABC≌⊿CDA
一组对边平行且相等的四边形是平行四边形.
已知:如图、在四边形ABCD中,AB∥CD、AB=CD.
求证:四边形ABCD是平行四边形.
证明:连接AC,
∵ AB//CD,
∴∠ACD = ∠CAB.
又AB =CD ,BD = DB,
∴△ABD ≌△CDB.
∴AD = CB.
∴四边形ABCD是平行四边形.
平行四边形的判定方法2
你还有其他证法吗?
数学语言:
∵ AD∥CB,AD= BC,
∴ 四边形ABCD是平行四边形.
读作:“AB平行且等于CD”.
平行四边形的判定定理2:
一组对边平行且相等的四边形是平行四边形.
“平行且相等”常用符号“ ”来表示.
AB∥CD且AB=CD,记作“AB CD”.
提炼概念
1、两组对边分别平行的四边形是平行四边形(定义).
2、两组对边分别相等的的四边形是平行四边形.
平行四边形的判定方法:
3、一组对边平行且相等的四边形是平行四边形.
典例精讲
例1、如图,在平行四边形ABCD中,E、F分别是边BC和AD上的两点,且AF=CE.
求证:四边形AECF为平行四边形.
B
A
C
D
F
E
你还有其他方法吗?
证明:∵四边形ABCD是平行四边形
∴AD//CB 即AF//CE
又∵AF=CE
∴四边形AECF是平行四边形
(一组对边平行且相等的四边形是平行四边形)
归纳概念
归纳:已知一组对边平行,要证四边形是平行四边形,证明的思路有如下两种:
1.证明另一组对边平行(平行四边形的定义);
2.证明平行的这组对边相等.
注:证明边相等通常需要利用三角形全等.
课堂练习
1.在四边形ABCD中:①AB//CD,②AD//BC,③AB=CD,④AD=BC,从以上选择两个条件使四边形ABCD为平行四边形的选法共有( )
A.3种 B.4种 C.5种 D.6种
B
2.如图,D是直线l外一点,在l上取两点A,B,连结AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连结CD,BC,则四边形ABCD是平行四边形,理由是 .
两组对边分别相等的四边形是平行四边形
3.如图,延长平行四边形ABCD的边AD到点F,使DF=DC,延长CB到点E,使BE=BA,连结AE,CF.求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,DC=BA.∴AF∥EC.
∵DF=DC,BE=BA,∴BE=DF,
∴AF=EC,∴四边形AECF是平行四边形,
∴AE=CF.
4.如图,AD∥BC,ED∥BF,且AF=CE.
求证:四边形ABCD 是平行四边形.
证明: ∵AD∥BC,ED∥BF,且AF=CE, ∴∠DAC=∠ACB,
∵∠DEF=∠EFB,AE=FC,∠AED=∠BFC,
∴△AED ≌ △BCF . ∴AD=BC.
四边形ABCD是平行四边形.
D
A
B
C
E
F
5.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形.
c
F
A
E
B
M
D
N
提示:可由等腰及折叠,从角度关系入手,由同旁内角互补得出两对边互相平行,从而得出四边形AEDF是平行四边形.
6.如图,小明剪成的一个等腰三角形纸片ABC,其AB=AC,他把∠B沿EM折叠使点B落在点D上,把∠C沿FN折叠使点C也落在点D上,则小明就说四边形AEDF是平行四边形,请你帮他说明理由.
课堂总结
判定 文字语言 图形语言 符号语言
定义 两组对边分别平行的四边形是平行四边形. ∵AB∥CD,AD∥BC,
∴是平行四边形.
定理1 两组对边分别相等的四边形是平等四边形. ∵AB=CD,AD= BC,
∴是平行四边形.
定理2 一组对边平行且相等的四边形是平等四边形. ∵AB∥CD,AB=CD,
∴是平行四边形.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
18.2.1平行四边形的判定(1)
华师大版 八年级 下册
教学目标
教学目标:1.理解并掌握“平行四边形的定义判定一个四边形是平行四
边形”.
2.理解并掌握“两组对边分别相等的四边形是平行四边形”.
3.理解并掌握“一组对边平行且相等的四边形是平行四边形”.
教学重点:平行四边形的判定方法及应用.
教学难点:平行四边形的判定定理的灵活应用.
新知导入
情境引入
一装潢店要招聘店员,老板出了这样一道考题:“一顾客要一张平行四边形的玻璃,你利用工具度量哪些数据可说明这张玻璃符合顾客要求.”
你能帮助他回答这个问题吗?
度量哪些数据?
两组对边的长度是否相等.
能说出理由吗?
新知讲解
合作学行四边形的这些性质,逆命题各是什么呢?
平行四边形两组对边分别平行.
平行四边形两组对边分别相等.
平行四边形对角线互相平分.
两组对边分别相等的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
平行四边形的判定方法(定义法)
两组对边分别相等的四边形.
1、任意取两点B,D.
2、分别以B,D为圆心,任意长为半径,分别在线段BD的两侧画弧.
3、再分别以B,D为圆心,适当长为半径画弧,与前面的两弧分别交与A,C两点.顺次连接各点,即得到两组对边分别相等的四边形ABCD.
这个四边形是平行四边形吗?
凭直觉和测量都确实感受到它是平行四边形我们如何用推理的方法加以证明呢?试一试吧!也许会成功
已知:在四边形ABCD中, AB=CD , AD=BC
求证:四边形ABCD 是平行四边形
证明思路
AB//CD, AD //BC
∠1=∠2,∠3=∠4
⊿ABC≌⊿CDA
两组对边分别相等的四边形是平行四边形.
已知:如图,在四边形ABCD中,AB=DC,AD=BC.
求证:四边形ABCD是平行四边形 .
证明:连结AC.
∵AD=BC,AB=DC,AC=AC,
∴△ABC≌ △ CDA(SSS),
∴∠1= ∠2,∠3=∠4 (全等三角形的性质).
∴AB∥CD,AD∥BC(内错角相等,两直线平行).
∴四边形ABCD是平行四边形.(两组对边分别平行的四边形是平行四边形)
平行四边形的判定方法1
两组对边分别相等的四边形是平行四边形.
平行四边形的判定定理1:
符号语言:
∵AB=CD,AD=BC.
∴四边形ABCD是平行四边形.
(两组对边分别相等的四边形是平行四边形)
如果知道了一组对边相等,那么再加上一个什么条件也可以得到一个平行四边形?
一组对边平行且相等的四边形是平行四边形.
一组对边平行,另一组对边相等的四边形是平行四边形.
一组对边平行且相等的四边形.
1、任意画两条平行线m,n.
2、在直线m,n上分别截取AB、CD,使AB、CD .
3、分别连结点B,C和点A,D.
这个四边形是平行四边形吗?
已知:如图、在四边形ABCD中,AB∥CD、AB=CD
求证:四边形ABCD是平行四边形
证明思路
AB∥CD, AD ∥BC
∠1=∠2,∠3=∠4
⊿ABC≌⊿CDA
一组对边平行且相等的四边形是平行四边形.
已知:如图、在四边形ABCD中,AB∥CD、AB=CD.
求证:四边形ABCD是平行四边形.
证明:连接AC,
∵ AB//CD,
∴∠ACD = ∠CAB.
又AB =CD ,BD = DB,
∴△ABD ≌△CDB.
∴AD = CB.
∴四边形ABCD是平行四边形.
平行四边形的判定方法2
你还有其他证法吗?
数学语言:
∵ AD∥CB,AD= BC,
∴ 四边形ABCD是平行四边形.
读作:“AB平行且等于CD”.
平行四边形的判定定理2:
一组对边平行且相等的四边形是平行四边形.
“平行且相等”常用符号“ ”来表示.
AB∥CD且AB=CD,记作“AB CD”.
提炼概念
1、两组对边分别平行的四边形是平行四边形(定义).
2、两组对边分别相等的的四边形是平行四边形.
平行四边形的判定方法:
3、一组对边平行且相等的四边形是平行四边形.
典例精讲
例1、如图,在平行四边形ABCD中,E、F分别是边BC和AD上的两点,且AF=CE.
求证:四边形AECF为平行四边形.
B
A
C
D
F
E
你还有其他方法吗?
证明:∵四边形ABCD是平行四边形
∴AD//CB 即AF//CE
又∵AF=CE
∴四边形AECF是平行四边形
(一组对边平行且相等的四边形是平行四边形)
归纳概念
归纳:已知一组对边平行,要证四边形是平行四边形,证明的思路有如下两种:
1.证明另一组对边平行(平行四边形的定义);
2.证明平行的这组对边相等.
注:证明边相等通常需要利用三角形全等.
课堂练习
1.在四边形ABCD中:①AB//CD,②AD//BC,③AB=CD,④AD=BC,从以上选择两个条件使四边形ABCD为平行四边形的选法共有( )
A.3种 B.4种 C.5种 D.6种
B
2.如图,D是直线l外一点,在l上取两点A,B,连结AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连结CD,BC,则四边形ABCD是平行四边形,理由是 .
两组对边分别相等的四边形是平行四边形
3.如图,延长平行四边形ABCD的边AD到点F,使DF=DC,延长CB到点E,使BE=BA,连结AE,CF.求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,DC=BA.∴AF∥EC.
∵DF=DC,BE=BA,∴BE=DF,
∴AF=EC,∴四边形AECF是平行四边形,
∴AE=CF.
4.如图,AD∥BC,ED∥BF,且AF=CE.
求证:四边形ABCD 是平行四边形.
证明: ∵AD∥BC,ED∥BF,且AF=CE, ∴∠DAC=∠ACB,
∵∠DEF=∠EFB,AE=FC,∠AED=∠BFC,
∴△AED ≌ △BCF . ∴AD=BC.
四边形ABCD是平行四边形.
D
A
B
C
E
F
5.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形.
c
F
A
E
B
M
D
N
提示:可由等腰及折叠,从角度关系入手,由同旁内角互补得出两对边互相平行,从而得出四边形AEDF是平行四边形.
6.如图,小明剪成的一个等腰三角形纸片ABC,其AB=AC,他把∠B沿EM折叠使点B落在点D上,把∠C沿FN折叠使点C也落在点D上,则小明就说四边形AEDF是平行四边形,请你帮他说明理由.
课堂总结
判定 文字语言 图形语言 符号语言
定义 两组对边分别平行的四边形是平行四边形. ∵AB∥CD,AD∥BC,
∴是平行四边形.
定理1 两组对边分别相等的四边形是平等四边形. ∵AB=CD,AD= BC,
∴是平行四边形.
定理2 一组对边平行且相等的四边形是平等四边形. ∵AB∥CD,AB=CD,
∴是平行四边形.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
