2022—2023学年北京课改版数学九年级下册 23.2 旋转变换 同步练习(含答案)
文档属性
| 名称 | 2022—2023学年北京课改版数学九年级下册 23.2 旋转变换 同步练习(含答案) |

|
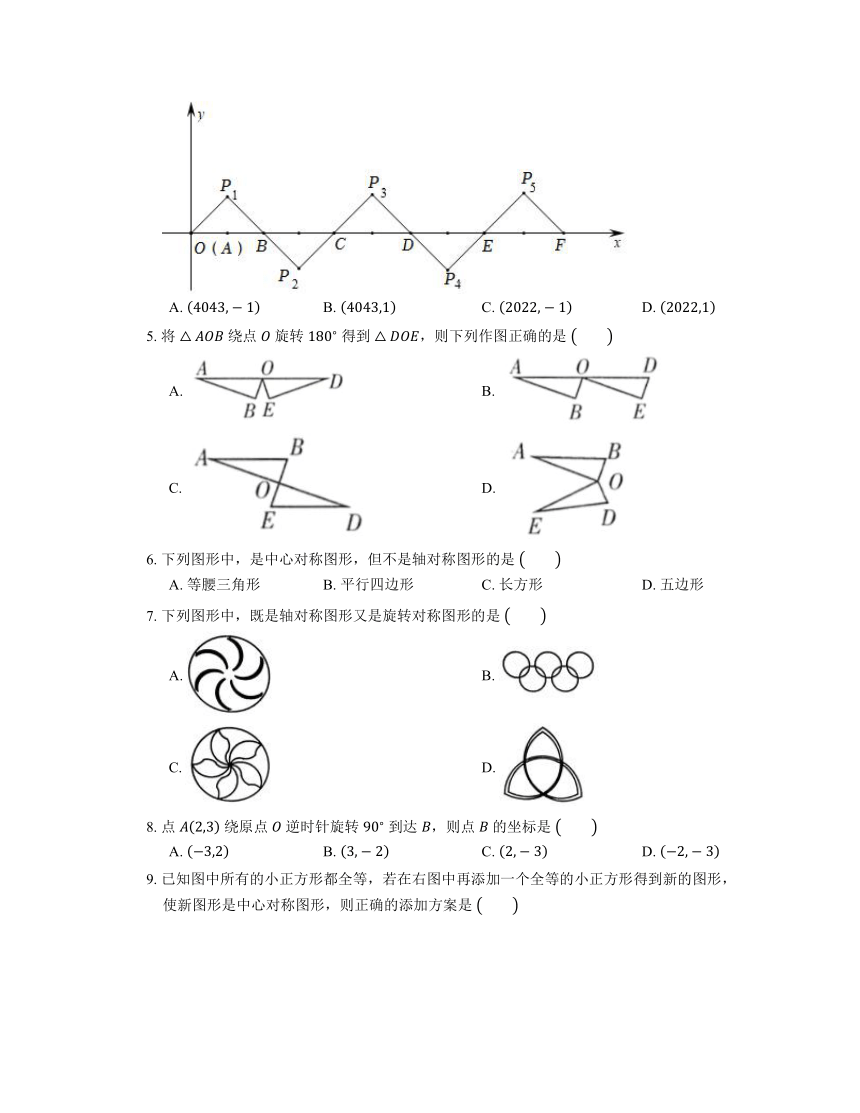
|
| 格式 | docx | ||
| 文件大小 | 556.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-03 15:15:06 | ||
图片预览


文档简介
北京课改版九下 23.2 旋转变换
一、选择题(共16小题)
1. 下面图形中,是中心对称图形但不是轴对称图形的是
A. B.
C. D.
2. 下列运动形式属于旋转的是
A. 在空中上升的氢气球 B. 飞驰的火车
C. 时钟上钟摆的摆动 D. 运动员掷出的标枪
3. 如图,在正方形网格中,将 绕点 旋转后得到 ,则下列旋转方式中,符合题意的是
A. 顺时针旋转 B. 逆时针旋转
C. 顺时针旋转 D. 逆时针旋转
4. 如图所示,在平面直角坐标系中,,, 是等腰直角三角形且 ,把 绕点 顺时针旋转 ,得到 ,把 绕点 顺时针旋转 ,得到 ,依此类推,得到的等腰直角三角形的直角顶点 的坐标为
A. B. C. D.
5. 将 绕点 旋转 得到 ,则下列作图正确的是
A. B.
C. D.
6. 下列图形中,是中心对称图形,但不是轴对称图形的是
A. 等腰三角形 B. 平行四边形 C. 长方形 D. 五边形
7. 下列图形中,既是轴对称图形又是旋转对称图形的是
A. B.
C. D.
8. 点 绕原点 逆时针旋转 到达 ,则点 的坐标是
A. B. C. D.
9. 已知图中所有的小正方形都全等,若在右图中再添加一个全等的小正方形得到新的图形,使新图形是中心对称图形,则正确的添加方案是
A. B.
C. D.
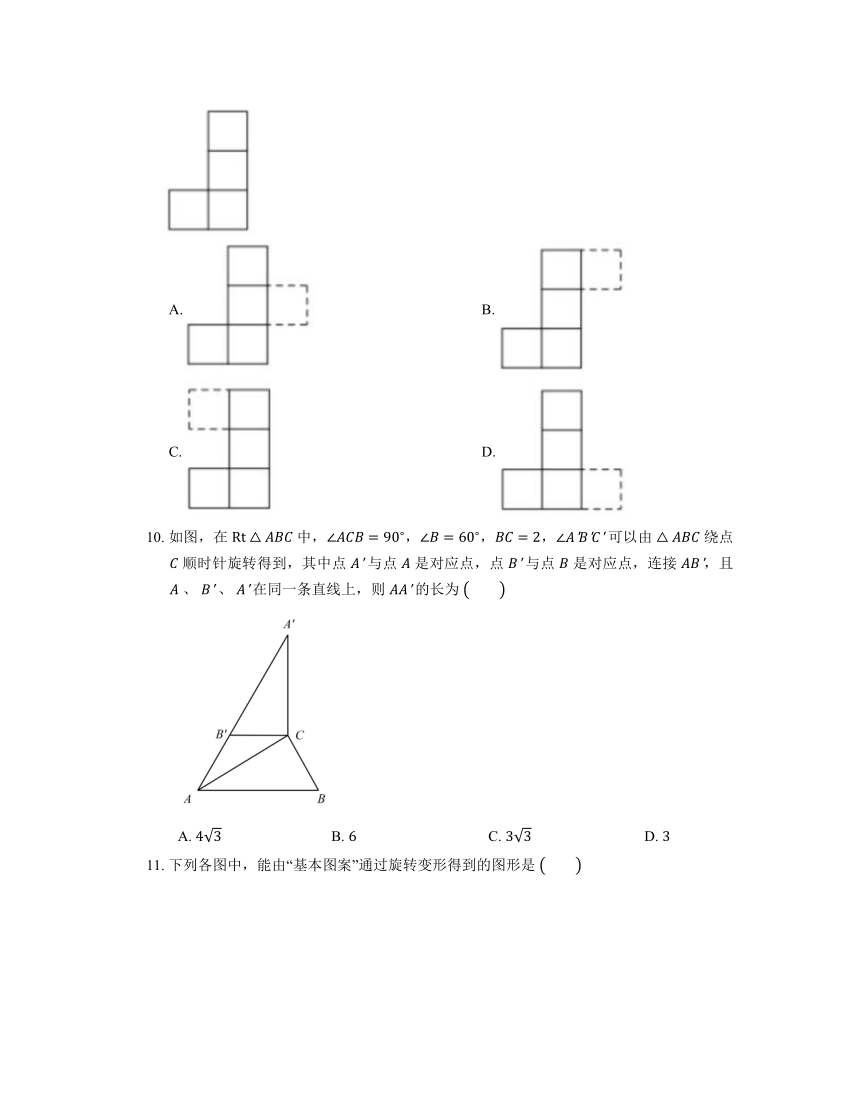
10. 如图,在 中,,,, 可以由 绕点 顺时针旋转得到,其中点 与点 是对应点,点 与点 是对应点,连接 ,且 、 、 在同一条直线上,则 的长为
A. B. C. D.
11. 下列各图中,能由“基本图案”通过旋转变形得到的图形是
A. B.
C. D.
12. 下列数学符号中,不是中心对称图形的是
A. B. C. D.
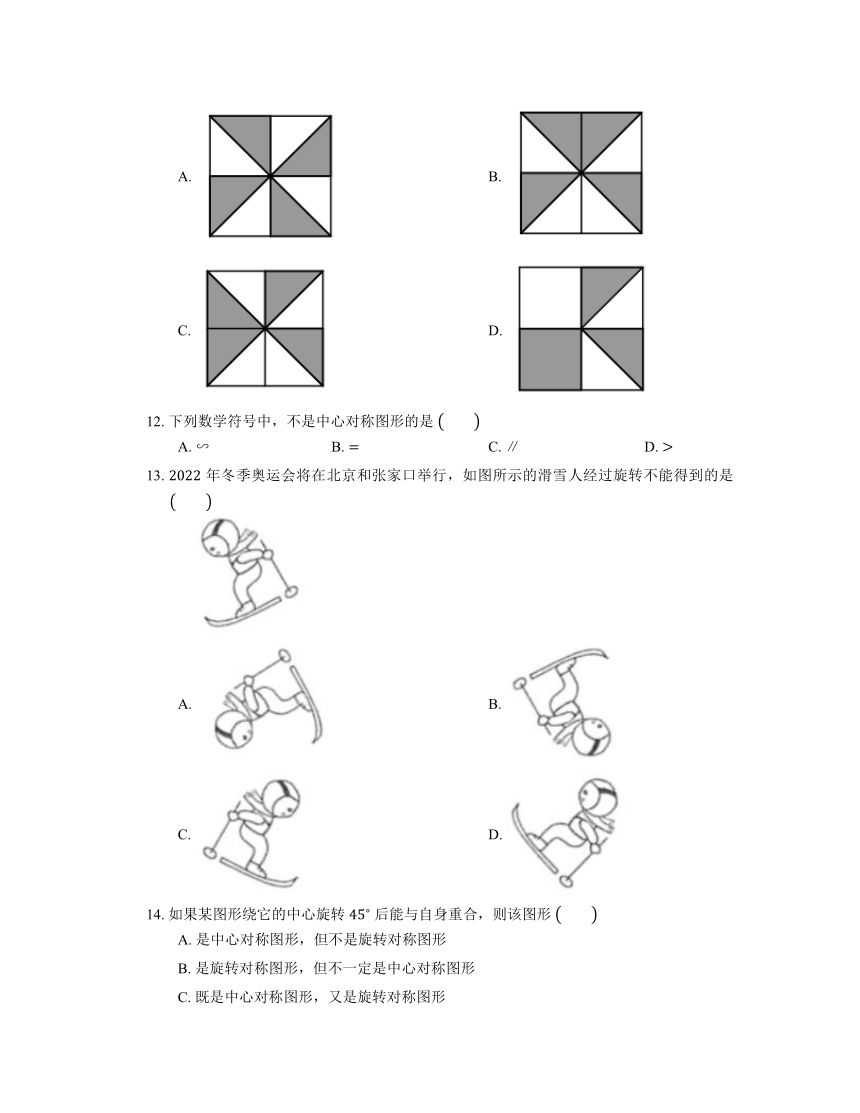
13. 年冬季奥运会将在北京和张家口举行,如图所示的滑雪人经过旋转不能得到的是
A. B.
C. D.
14. 如果某图形绕它的中心旋转 后能与自身重合,则该图形
A. 是中心对称图形,但不是旋转对称图形
B. 是旋转对称图形,但不一定是中心对称图形
C. 既是中心对称图形,又是旋转对称图形
D. 既不是中心对称图形,也不是旋转对称图形
15. 已知:点 ,将点 绕原点逆时针旋转 ,得到点 ,则点 的坐标是
A. B. C. D.
16. 关于中心对称的两个图形的对称中心,下列说法正确的是
A. 两个图形的交点
B. 连接两对对应点,两条线段所在直线的交点
C. 对应角的角平分线交点
D. 两条对应线段所在直线的交点
二、填空题(共9小题)
17. 在平面内,如果一个图形绕着一个定点旋转一定大小的角 后,能与原图形重合,那么这个图形叫做 ,这个定点叫做 ,角 叫做 .
18. 与点 ( 不为零)关于原点 对称的点的坐标是 .
19. 若两个图形成中心对称,分别联结这两个图形的两对对应点,所得两条直线的交点就是 .
20. 一个图形绕着一个定点转动一个角度后与原来图形 ,这样的图形叫做旋转对称图形.一个图形绕着某一点旋转 ,如果旋转后的图形与原来的图形重合,那么这个图形叫做 对称图形,这个点叫做对称中心.
21. 在平面内,将一个图形上的所有点绕一个定点按照某个方向转动一个角度,这种运动叫做 ,这个定点叫做 ,图形转动的角度叫做 .图形旋转时,图形中的每一点旋转的角度都 ,都等于图形的 ;每个点到旋转中心的距离在旋转过程中都保持 .
22. 下列图中是中心对称图形的有 .
23. 如图,在正方形网格中,线段 可以看作是线段 经过若干次图形的变化(平移、旋转、轴对称)得到的,写出一种由线段 得到线段 的过程: .
24. 下列图形中,是旋转对称图形的,请在相应的括号内,写出该图形旋转角的最小度数.
25. 点 关于原点对称的点在第 象限,它的坐标是 .
三、解答题(共7小题)
26. 如图,点 为坐标原点,点 的坐标是 ,以点 和点 为顶点在直角坐标平面内画正方形,符合这样条件的正方形可以有几个 写出符合条件的正方形的第三个顶点、第四个顶点的坐标.
27. 如图,将等腰直角 (其中 度)进行如下运动,请依次画出运动后的图形.
(1)以点 为旋转中心,顺时针旋转 度.
(2)以点 为旋转中心,逆时针旋转 度.
(3)以点 为旋转中心,旋转 度.
(4)以线段 的中点为旋转中心,旋转 度.
28. 在图中网格上按要求画出图形,并回答问题:
(1)先画出 关于直线 的轴对称图形 ,再画出 关于直线 的轴对称图形 .
(2)在()的条件下,请判断 与 的位置关系为 .
29. 画出一个旋转角为 的旋转对称图形.
30. 观察下列图形,将其中的旋转对称图形和中心对称图形所对应的编号填入相应的横线里.
(1)旋转对称图形 .
(2)中心对称图形 .
31. 请把下面这个图形补画成中心对称图形,并用点 表示对称中心(最少画三个).
32. 四边形 中,,, 于点 .点 是线段 延长线上一点, 绕某一点逆时针旋转后与 重合.
(1)图中旋转中心是点 ,点 的对应点是点 ,点 的对应点是点 ;
(2)写出图中所有相等的锐角以及 的度数,并说明理由.
答案
1. A
【解析】在平面内,把一个图形绕着某个点旋转 ,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.轴对称图形的定义为:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形.直线叫做对称轴.
根据中心对称图形和轴对称图形的定义可知:
A选项:图形是中心对称图形,不是轴对称图形,符合题意,故A正确;
B选项:图形既不是中心对称图形,也不是轴对称图形,不符合题意,故B错误;
C选项:图形既是中心对称图形,也是轴对称图形,不符合题意,故C错误;
D选项:图形是中心对称图形,不是轴对称图形,不符合题意,故D错误.
2. C
【解析】A.在空中上升的氢气球是平移,故此选项不符合题意;
B.飞驰的火车是平移,故此选项不符合题意;
C.时钟上钟摆的摆动,属于旋转,故此选项符合题意;
D.运动员掷出的标枪是平移,故此选项不符合题意.
故选C.
3. B
4. A
【解析】,, 是等腰直角三角形,且 ,
.
把 绕点 顺时针旋转 ,得到 ,
.
同理可得出:,,,,
,( 为自然数).
,,
.
故选:A.
5. C
6. B
7. D
8. A
9. B
【解析】A、新图形不是中心对称图形,故此选项错误;
B、新图形是中心对称图形,故此选项正确;
C、新图形不是中心对称图形,故此选项错误;
D、新图形不是中心对称图形,故此选项错误;
故选:B.
10. B
11. A
12. D
13. C
【解析】选项A、B、D中滑雪人都可以通过题图旋转得到,而选项C中滑雪人是题图通过翻折到的.
14. C
15. B
16. B
17. 旋转对称图形,旋转对称中心,旋转角
18.
19. 对称中心
20. 重合,中心
21. 图形的旋转,旋转中心,旋转角,相等,旋转角,不变
22. (1),(3)
23. 将线段 绕点 逆时针旋转 ,再向左平移 个单位长度
24. ,,,
25. 二,
26.
, 或 , 或 ,.
27. (1) 略
(2) 略
(3) 略
(4) 略
28. (1) 图略
(2) 关于点 成中心对称
29. 正方形等.
30. (1) A,B,C,D,E
(2) C,D
31.
32. (1) ;;
(2) ,,旋转图形的对应角大小相等;,因为 , 是旋转角,所以 .
一、选择题(共16小题)
1. 下面图形中,是中心对称图形但不是轴对称图形的是
A. B.
C. D.
2. 下列运动形式属于旋转的是
A. 在空中上升的氢气球 B. 飞驰的火车
C. 时钟上钟摆的摆动 D. 运动员掷出的标枪
3. 如图,在正方形网格中,将 绕点 旋转后得到 ,则下列旋转方式中,符合题意的是
A. 顺时针旋转 B. 逆时针旋转
C. 顺时针旋转 D. 逆时针旋转
4. 如图所示,在平面直角坐标系中,,, 是等腰直角三角形且 ,把 绕点 顺时针旋转 ,得到 ,把 绕点 顺时针旋转 ,得到 ,依此类推,得到的等腰直角三角形的直角顶点 的坐标为
A. B. C. D.
5. 将 绕点 旋转 得到 ,则下列作图正确的是
A. B.
C. D.
6. 下列图形中,是中心对称图形,但不是轴对称图形的是
A. 等腰三角形 B. 平行四边形 C. 长方形 D. 五边形
7. 下列图形中,既是轴对称图形又是旋转对称图形的是
A. B.
C. D.
8. 点 绕原点 逆时针旋转 到达 ,则点 的坐标是
A. B. C. D.
9. 已知图中所有的小正方形都全等,若在右图中再添加一个全等的小正方形得到新的图形,使新图形是中心对称图形,则正确的添加方案是
A. B.
C. D.
10. 如图,在 中,,,, 可以由 绕点 顺时针旋转得到,其中点 与点 是对应点,点 与点 是对应点,连接 ,且 、 、 在同一条直线上,则 的长为
A. B. C. D.
11. 下列各图中,能由“基本图案”通过旋转变形得到的图形是
A. B.
C. D.
12. 下列数学符号中,不是中心对称图形的是
A. B. C. D.
13. 年冬季奥运会将在北京和张家口举行,如图所示的滑雪人经过旋转不能得到的是
A. B.
C. D.
14. 如果某图形绕它的中心旋转 后能与自身重合,则该图形
A. 是中心对称图形,但不是旋转对称图形
B. 是旋转对称图形,但不一定是中心对称图形
C. 既是中心对称图形,又是旋转对称图形
D. 既不是中心对称图形,也不是旋转对称图形
15. 已知:点 ,将点 绕原点逆时针旋转 ,得到点 ,则点 的坐标是
A. B. C. D.
16. 关于中心对称的两个图形的对称中心,下列说法正确的是
A. 两个图形的交点
B. 连接两对对应点,两条线段所在直线的交点
C. 对应角的角平分线交点
D. 两条对应线段所在直线的交点
二、填空题(共9小题)
17. 在平面内,如果一个图形绕着一个定点旋转一定大小的角 后,能与原图形重合,那么这个图形叫做 ,这个定点叫做 ,角 叫做 .
18. 与点 ( 不为零)关于原点 对称的点的坐标是 .
19. 若两个图形成中心对称,分别联结这两个图形的两对对应点,所得两条直线的交点就是 .
20. 一个图形绕着一个定点转动一个角度后与原来图形 ,这样的图形叫做旋转对称图形.一个图形绕着某一点旋转 ,如果旋转后的图形与原来的图形重合,那么这个图形叫做 对称图形,这个点叫做对称中心.
21. 在平面内,将一个图形上的所有点绕一个定点按照某个方向转动一个角度,这种运动叫做 ,这个定点叫做 ,图形转动的角度叫做 .图形旋转时,图形中的每一点旋转的角度都 ,都等于图形的 ;每个点到旋转中心的距离在旋转过程中都保持 .
22. 下列图中是中心对称图形的有 .
23. 如图,在正方形网格中,线段 可以看作是线段 经过若干次图形的变化(平移、旋转、轴对称)得到的,写出一种由线段 得到线段 的过程: .
24. 下列图形中,是旋转对称图形的,请在相应的括号内,写出该图形旋转角的最小度数.
25. 点 关于原点对称的点在第 象限,它的坐标是 .
三、解答题(共7小题)
26. 如图,点 为坐标原点,点 的坐标是 ,以点 和点 为顶点在直角坐标平面内画正方形,符合这样条件的正方形可以有几个 写出符合条件的正方形的第三个顶点、第四个顶点的坐标.
27. 如图,将等腰直角 (其中 度)进行如下运动,请依次画出运动后的图形.
(1)以点 为旋转中心,顺时针旋转 度.
(2)以点 为旋转中心,逆时针旋转 度.
(3)以点 为旋转中心,旋转 度.
(4)以线段 的中点为旋转中心,旋转 度.
28. 在图中网格上按要求画出图形,并回答问题:
(1)先画出 关于直线 的轴对称图形 ,再画出 关于直线 的轴对称图形 .
(2)在()的条件下,请判断 与 的位置关系为 .
29. 画出一个旋转角为 的旋转对称图形.
30. 观察下列图形,将其中的旋转对称图形和中心对称图形所对应的编号填入相应的横线里.
(1)旋转对称图形 .
(2)中心对称图形 .
31. 请把下面这个图形补画成中心对称图形,并用点 表示对称中心(最少画三个).
32. 四边形 中,,, 于点 .点 是线段 延长线上一点, 绕某一点逆时针旋转后与 重合.
(1)图中旋转中心是点 ,点 的对应点是点 ,点 的对应点是点 ;
(2)写出图中所有相等的锐角以及 的度数,并说明理由.
答案
1. A
【解析】在平面内,把一个图形绕着某个点旋转 ,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.轴对称图形的定义为:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形.直线叫做对称轴.
根据中心对称图形和轴对称图形的定义可知:
A选项:图形是中心对称图形,不是轴对称图形,符合题意,故A正确;
B选项:图形既不是中心对称图形,也不是轴对称图形,不符合题意,故B错误;
C选项:图形既是中心对称图形,也是轴对称图形,不符合题意,故C错误;
D选项:图形是中心对称图形,不是轴对称图形,不符合题意,故D错误.
2. C
【解析】A.在空中上升的氢气球是平移,故此选项不符合题意;
B.飞驰的火车是平移,故此选项不符合题意;
C.时钟上钟摆的摆动,属于旋转,故此选项符合题意;
D.运动员掷出的标枪是平移,故此选项不符合题意.
故选C.
3. B
4. A
【解析】,, 是等腰直角三角形,且 ,
.
把 绕点 顺时针旋转 ,得到 ,
.
同理可得出:,,,,
,( 为自然数).
,,
.
故选:A.
5. C
6. B
7. D
8. A
9. B
【解析】A、新图形不是中心对称图形,故此选项错误;
B、新图形是中心对称图形,故此选项正确;
C、新图形不是中心对称图形,故此选项错误;
D、新图形不是中心对称图形,故此选项错误;
故选:B.
10. B
11. A
12. D
13. C
【解析】选项A、B、D中滑雪人都可以通过题图旋转得到,而选项C中滑雪人是题图通过翻折到的.
14. C
15. B
16. B
17. 旋转对称图形,旋转对称中心,旋转角
18.
19. 对称中心
20. 重合,中心
21. 图形的旋转,旋转中心,旋转角,相等,旋转角,不变
22. (1),(3)
23. 将线段 绕点 逆时针旋转 ,再向左平移 个单位长度
24. ,,,
25. 二,
26.
, 或 , 或 ,.
27. (1) 略
(2) 略
(3) 略
(4) 略
28. (1) 图略
(2) 关于点 成中心对称
29. 正方形等.
30. (1) A,B,C,D,E
(2) C,D
31.
32. (1) ;;
(2) ,,旋转图形的对应角大小相等;,因为 , 是旋转角,所以 .
