第二十四章 投影、视图与展开图 单元综合练(含答案) 2022-2023学年京改版九年级数学下册
文档属性
| 名称 | 第二十四章 投影、视图与展开图 单元综合练(含答案) 2022-2023学年京改版九年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 595.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-03 16:37:00 | ||
图片预览



文档简介
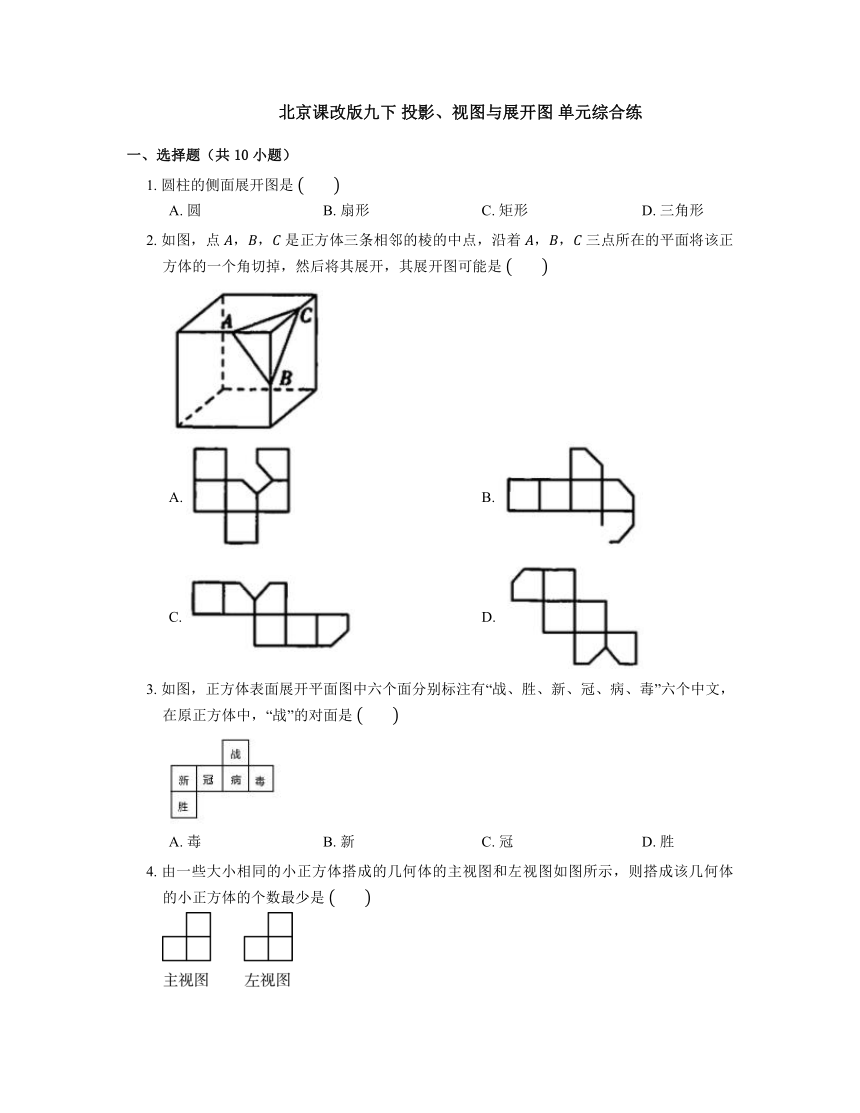
北京课改版九下 投影、视图与展开图 单元综合练
一、选择题(共10小题)
1. 圆柱的侧面展开图是
A. 圆 B. 扇形 C. 矩形 D. 三角形
2. 如图,点 ,, 是正方体三条相邻的棱的中点,沿着 ,, 三点所在的平面将该正方体的一个角切掉,然后将其展开,其展开图可能是
A. B.
C. D.
3. 如图,正方体表面展开平面图中六个面分别标注有“战、胜、新、冠、病、毒”六个中文,在原正方体中,“战”的对面是
A. 毒 B. 新 C. 冠 D. 胜
4. 由一些大小相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体的小正方体的个数最少是
A. B. C. D.
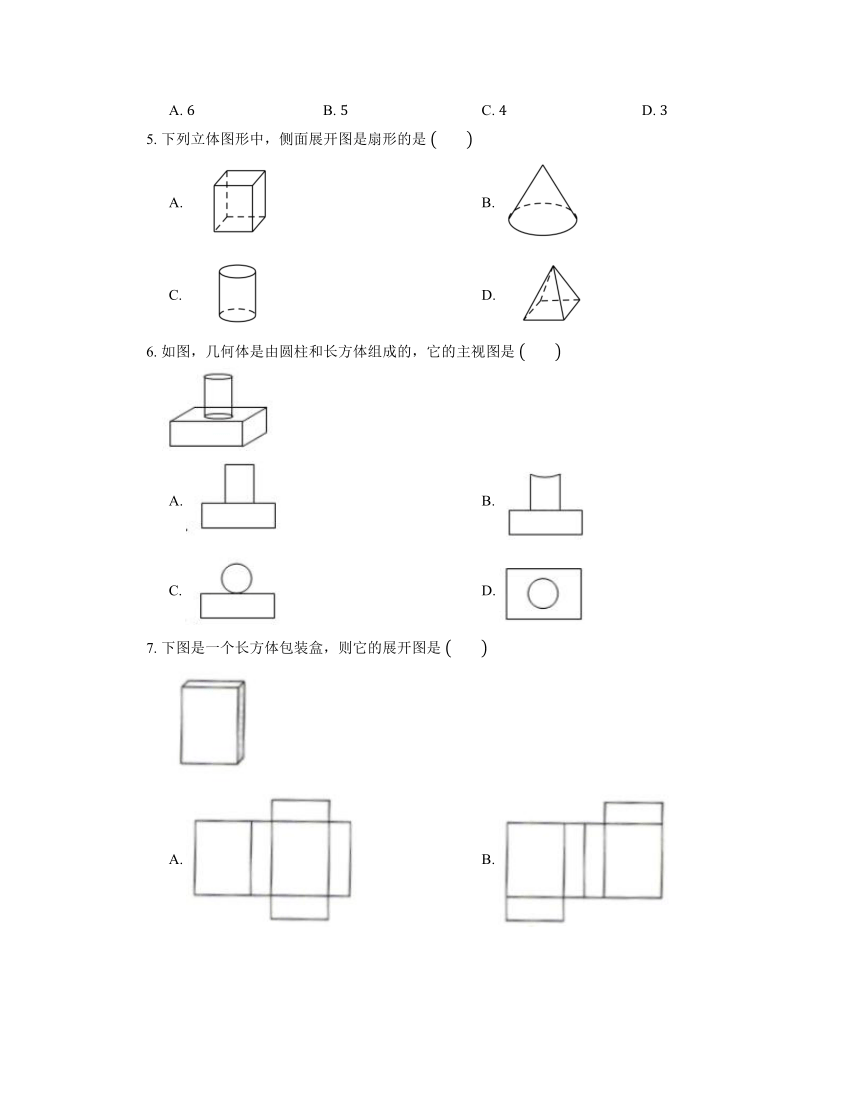
5. 下列立体图形中,侧面展开图是扇形的是
A. B.
C. D.
6. 如图,几何体是由圆柱和长方体组成的,它的主视图是
A. B.
C. D.
7. 下图是一个长方体包装盒,则它的展开图是
A. B.
C. D.
8. 下面四个立体图形中,从正面观察是三角形的是
A. B.
C. D.
9. 如图,是一个几何体从正面、左面、上面看得到的图形,则这个几何体是
A. B.
C. D.
10. 如图,已知 是圆柱底面的直径, 是圆柱的高,在圆柱的侧面上,过点 , 嵌有一圈路径最短的金属丝,现将圆柱侧面沿 剪开,所得的圆柱侧面展开图是
A. B.
C. D.
二、填空题(共6小题)
11. 在下列横线中写出如图所示这个物体的三个视图的名称.
12. 观察一个长方体,最多能看到它的 个面,最少能看到 个面.
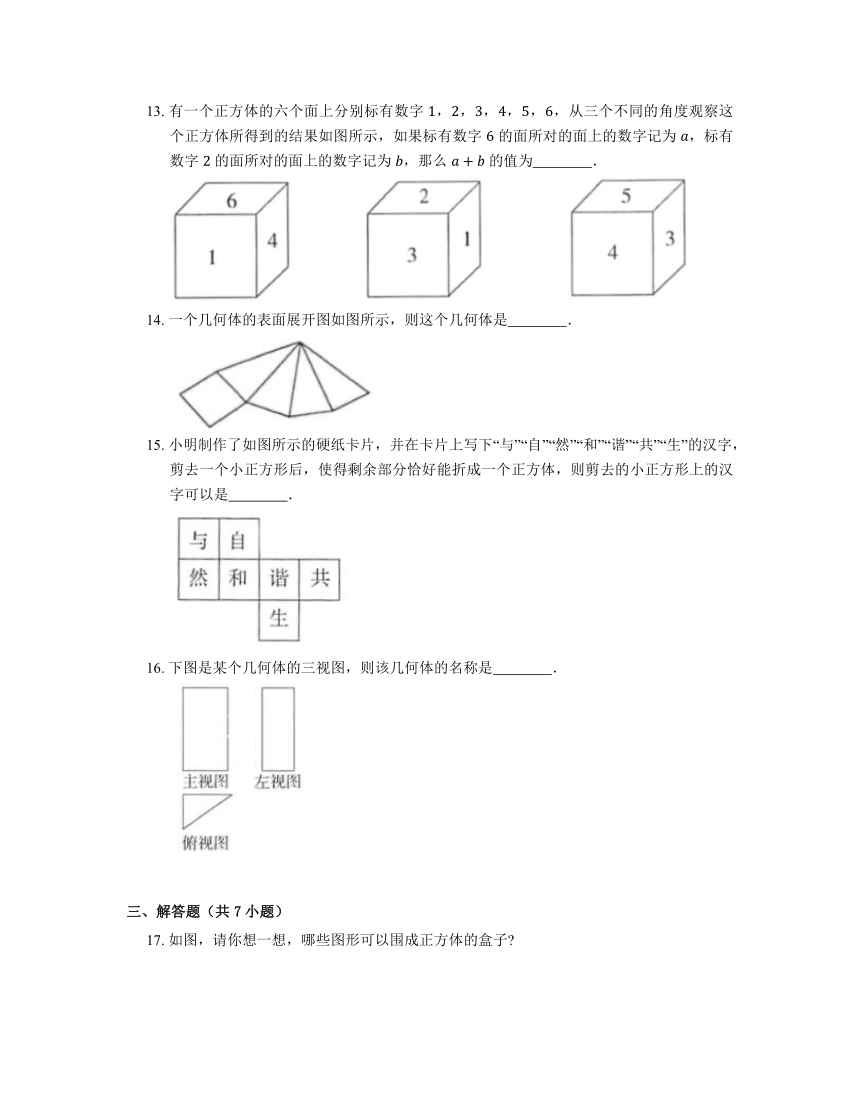
13. 有一个正方体的六个面上分别标有数字 ,,,,,,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字 的面所对的面上的数字记为 ,标有数字 的面所对的面上的数字记为 ,那么 的值为 .
14. 一个几何体的表面展开图如图所示,则这个几何体是 .
15. 小明制作了如图所示的硬纸卡片,并在卡片上写下“与”“自”“然”“和”“谐”“共”“生”的汉字,剪去一个小正方形后,使得剩余部分恰好能折成一个正方体,则剪去的小正方形上的汉字可以是 .
16. 下图是某个几何体的三视图,则该几何体的名称是 .
三、解答题(共7小题)
17. 如图,请你想一想,哪些图形可以围成正方体的盒子
18. 如图是一个几何体的三视图.
(1)写出这个几何体的名称: ;
(2)画出它的一种表面展开图;
(3)求这个几何体的侧面积.
19. 如图所示,在正方体能看见的面上写上数字 ,,,而在表面展开图中也已分别写上了两个或一个指定的数.请你在表面展开图的其他各面上写上适当的数,使得相对的面上两数的和等于 .
20. 如图,六个平面图形中,有圆柱、圆锥、三棱柱(它的底面是三边相等的三角形)的表面展开图,请你把立体图形与它的表面展开图用线连起来(不考虑尺寸).
21. 一个零件是由长为 、高和宽都为 的长方体与直径为 、高度为 的半圆柱组成几何体后,又切去直径为 的圆柱后剩下的几何体,其实物直观图如图所示,请画出这个零件的三视图.
22. 有两张长为 ,宽为 的长方形硬纸板 ,,如果在 的四个角上各截去一个边长为 的正方形,如图①所示;在 的四个角上各截去一个边长为 的正方形,如图②所示,然后把它们分别折叠成一个无盖的长方体小盒,请问哪个硬纸板折叠成的小盒容积较大 为什么
23. 如图是一个几何体的三视图(单位:厘米).
(1)写出这个几何体的名称;
(2)如果一只蚂蚁要从这个几何体中的点 出发,沿表面爬到 的中点 ,请你求出这个线路的最短路程.
答案
1. C
2. D
【解析】选项A、B、C折叠后都不符合题意,只有选项D折叠后两个剪去的三角形与另一个剪去的三角形分别交于一个顶点,与正方体三个剪去的三角形分别交于一个顶点符合.
3. D
【解析】战对胜,新对病,冠对毒.
4. D
【解析】仔细观察物体的主视图和左视图可知:该几何体的下面最少要有 个小正方体,上面最少要有 个小正方体,
故该几何体最少有 个小正方体组成.
5. B
【解析】圆锥的侧面展开图是扇形.
6. A
【解析】从正面看下面是一个比较长的矩形,上面是一个比较窄的矩形.
7. A
8. C
9. B
【解析】观察从正面、左面、上面看得到的图形发现,这个几何体是长方体和圆锥的组合图形.故选B.
10. A
【解析】因圆柱的展开面为长方形, 展开应该是两线段,且有公共点 .
11. 主视图,俯视图,左视图
12. ,
13.
【解析】由题图可知,与 相邻的面上的数字有 ,,,,
所以标有数字 的面所对的面上的数字是 ,
因为与 相邻的面上的数字有 ,,,,
所以标有数字 的面所对的面上的数字是 ,
所以标有数字 的面所对的面上的数字是 ,
又因为标有数字 的面所对的面上的数字记为 ,标有数字 的面所对的面上的数字记为 ,
所以 ,,
所以 .
14. 四棱锥
15. “与”或“自”或“然”
【解析】因为剩余的部分恰好能折成一个正方体,所以展开图中没有“田”字形,所以应剪去写有“与“或”自”或“然”的小正方形.
16. 三棱柱
【解析】由主视图和左视图为矩形可得该几何体是柱体,由俯视图是三角形可得该几何体是三棱柱.
17. ()()()
18. (1) 三棱柱
(2) 表面展开图如图所示(答案不唯一).
(3) ,
这个几何体的侧面积为 .
19. 如图.(答案不唯一)
20. 连线如下:
21. 三视图如图所示:
22. 硬纸板 折叠成的小盒容积较大.
理由:硬纸板 折叠成的小盒容积为 .
硬纸板 折叠成的小盒容积为 ,
因为 ,
所以硬纸板 折叠成的小盒容积较大.
23. (1) 圆锥.
(2) 如图将圆锥侧面展开,线段 为所求的最短路程.
由条件得:, 为弧 的中点,
易得 厘米.
一、选择题(共10小题)
1. 圆柱的侧面展开图是
A. 圆 B. 扇形 C. 矩形 D. 三角形
2. 如图,点 ,, 是正方体三条相邻的棱的中点,沿着 ,, 三点所在的平面将该正方体的一个角切掉,然后将其展开,其展开图可能是
A. B.
C. D.
3. 如图,正方体表面展开平面图中六个面分别标注有“战、胜、新、冠、病、毒”六个中文,在原正方体中,“战”的对面是
A. 毒 B. 新 C. 冠 D. 胜
4. 由一些大小相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体的小正方体的个数最少是
A. B. C. D.
5. 下列立体图形中,侧面展开图是扇形的是
A. B.
C. D.
6. 如图,几何体是由圆柱和长方体组成的,它的主视图是
A. B.
C. D.
7. 下图是一个长方体包装盒,则它的展开图是
A. B.
C. D.
8. 下面四个立体图形中,从正面观察是三角形的是
A. B.
C. D.
9. 如图,是一个几何体从正面、左面、上面看得到的图形,则这个几何体是
A. B.
C. D.
10. 如图,已知 是圆柱底面的直径, 是圆柱的高,在圆柱的侧面上,过点 , 嵌有一圈路径最短的金属丝,现将圆柱侧面沿 剪开,所得的圆柱侧面展开图是
A. B.
C. D.
二、填空题(共6小题)
11. 在下列横线中写出如图所示这个物体的三个视图的名称.
12. 观察一个长方体,最多能看到它的 个面,最少能看到 个面.
13. 有一个正方体的六个面上分别标有数字 ,,,,,,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字 的面所对的面上的数字记为 ,标有数字 的面所对的面上的数字记为 ,那么 的值为 .
14. 一个几何体的表面展开图如图所示,则这个几何体是 .
15. 小明制作了如图所示的硬纸卡片,并在卡片上写下“与”“自”“然”“和”“谐”“共”“生”的汉字,剪去一个小正方形后,使得剩余部分恰好能折成一个正方体,则剪去的小正方形上的汉字可以是 .
16. 下图是某个几何体的三视图,则该几何体的名称是 .
三、解答题(共7小题)
17. 如图,请你想一想,哪些图形可以围成正方体的盒子
18. 如图是一个几何体的三视图.
(1)写出这个几何体的名称: ;
(2)画出它的一种表面展开图;
(3)求这个几何体的侧面积.
19. 如图所示,在正方体能看见的面上写上数字 ,,,而在表面展开图中也已分别写上了两个或一个指定的数.请你在表面展开图的其他各面上写上适当的数,使得相对的面上两数的和等于 .
20. 如图,六个平面图形中,有圆柱、圆锥、三棱柱(它的底面是三边相等的三角形)的表面展开图,请你把立体图形与它的表面展开图用线连起来(不考虑尺寸).
21. 一个零件是由长为 、高和宽都为 的长方体与直径为 、高度为 的半圆柱组成几何体后,又切去直径为 的圆柱后剩下的几何体,其实物直观图如图所示,请画出这个零件的三视图.
22. 有两张长为 ,宽为 的长方形硬纸板 ,,如果在 的四个角上各截去一个边长为 的正方形,如图①所示;在 的四个角上各截去一个边长为 的正方形,如图②所示,然后把它们分别折叠成一个无盖的长方体小盒,请问哪个硬纸板折叠成的小盒容积较大 为什么
23. 如图是一个几何体的三视图(单位:厘米).
(1)写出这个几何体的名称;
(2)如果一只蚂蚁要从这个几何体中的点 出发,沿表面爬到 的中点 ,请你求出这个线路的最短路程.
答案
1. C
2. D
【解析】选项A、B、C折叠后都不符合题意,只有选项D折叠后两个剪去的三角形与另一个剪去的三角形分别交于一个顶点,与正方体三个剪去的三角形分别交于一个顶点符合.
3. D
【解析】战对胜,新对病,冠对毒.
4. D
【解析】仔细观察物体的主视图和左视图可知:该几何体的下面最少要有 个小正方体,上面最少要有 个小正方体,
故该几何体最少有 个小正方体组成.
5. B
【解析】圆锥的侧面展开图是扇形.
6. A
【解析】从正面看下面是一个比较长的矩形,上面是一个比较窄的矩形.
7. A
8. C
9. B
【解析】观察从正面、左面、上面看得到的图形发现,这个几何体是长方体和圆锥的组合图形.故选B.
10. A
【解析】因圆柱的展开面为长方形, 展开应该是两线段,且有公共点 .
11. 主视图,俯视图,左视图
12. ,
13.
【解析】由题图可知,与 相邻的面上的数字有 ,,,,
所以标有数字 的面所对的面上的数字是 ,
因为与 相邻的面上的数字有 ,,,,
所以标有数字 的面所对的面上的数字是 ,
所以标有数字 的面所对的面上的数字是 ,
又因为标有数字 的面所对的面上的数字记为 ,标有数字 的面所对的面上的数字记为 ,
所以 ,,
所以 .
14. 四棱锥
15. “与”或“自”或“然”
【解析】因为剩余的部分恰好能折成一个正方体,所以展开图中没有“田”字形,所以应剪去写有“与“或”自”或“然”的小正方形.
16. 三棱柱
【解析】由主视图和左视图为矩形可得该几何体是柱体,由俯视图是三角形可得该几何体是三棱柱.
17. ()()()
18. (1) 三棱柱
(2) 表面展开图如图所示(答案不唯一).
(3) ,
这个几何体的侧面积为 .
19. 如图.(答案不唯一)
20. 连线如下:
21. 三视图如图所示:
22. 硬纸板 折叠成的小盒容积较大.
理由:硬纸板 折叠成的小盒容积为 .
硬纸板 折叠成的小盒容积为 ,
因为 ,
所以硬纸板 折叠成的小盒容积较大.
23. (1) 圆锥.
(2) 如图将圆锥侧面展开,线段 为所求的最短路程.
由条件得:, 为弧 的中点,
易得 厘米.
