12.2.2与三角形内角和有关的证明(含答案)2022-2023学年苏科版七年级下册数学
文档属性
| 名称 | 12.2.2与三角形内角和有关的证明(含答案)2022-2023学年苏科版七年级下册数学 |  | |
| 格式 | docx | ||
| 文件大小 | 86.8KB | ||
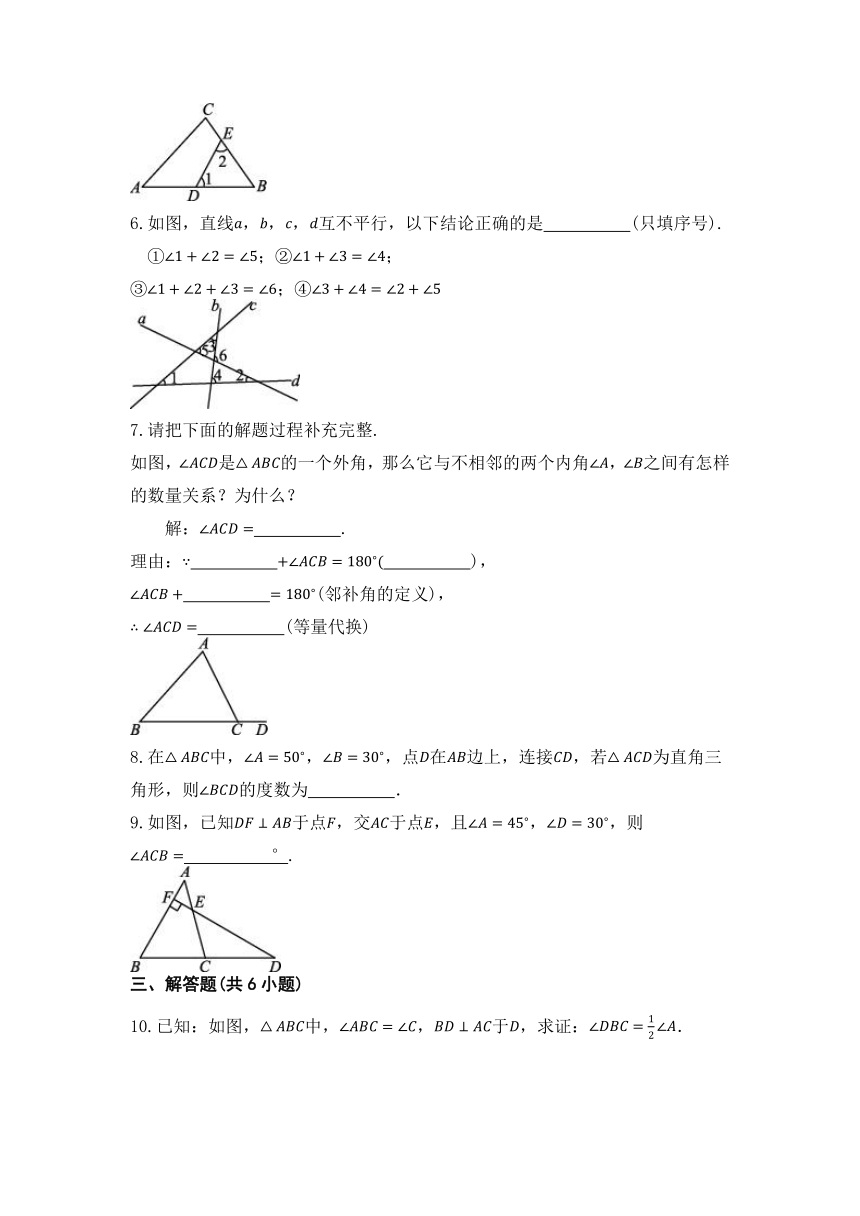
| 资源类型 | 教案 | ||
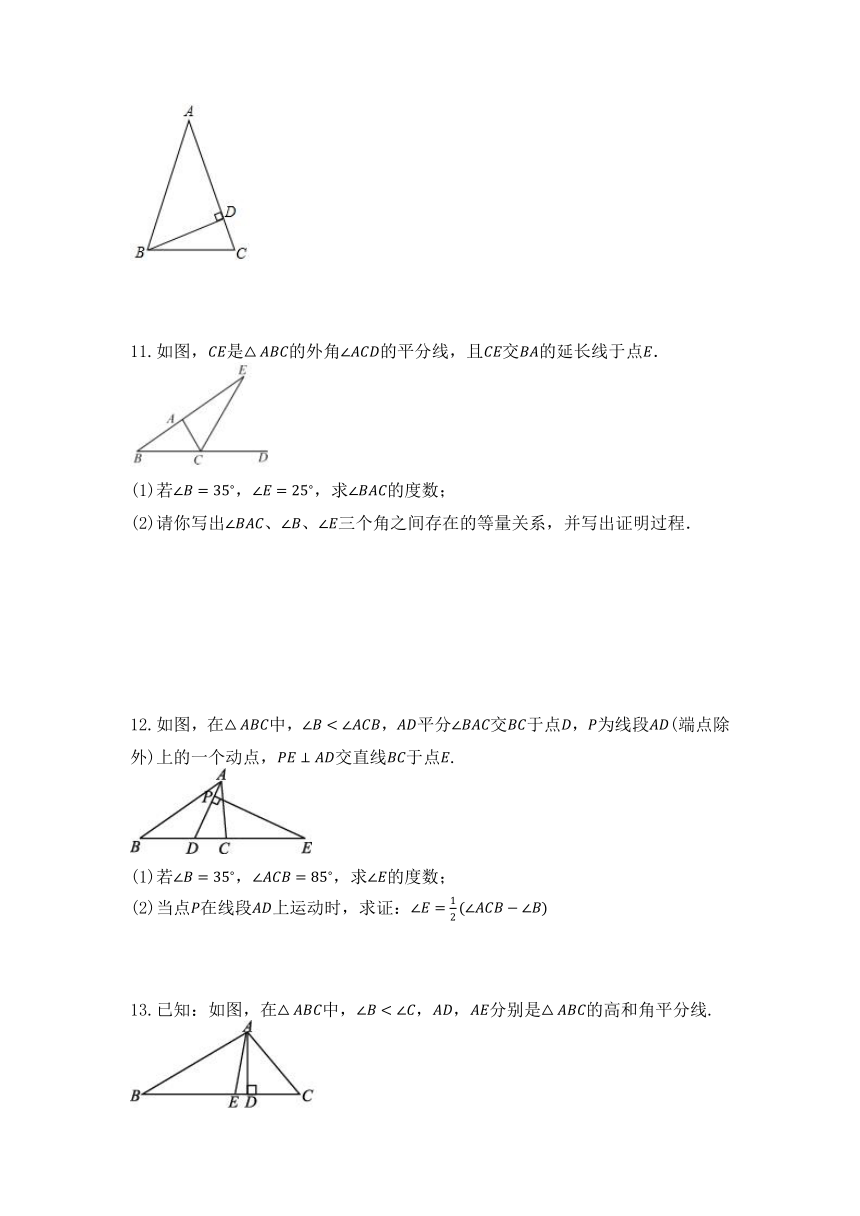
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-03 16:39:31 | ||
图片预览

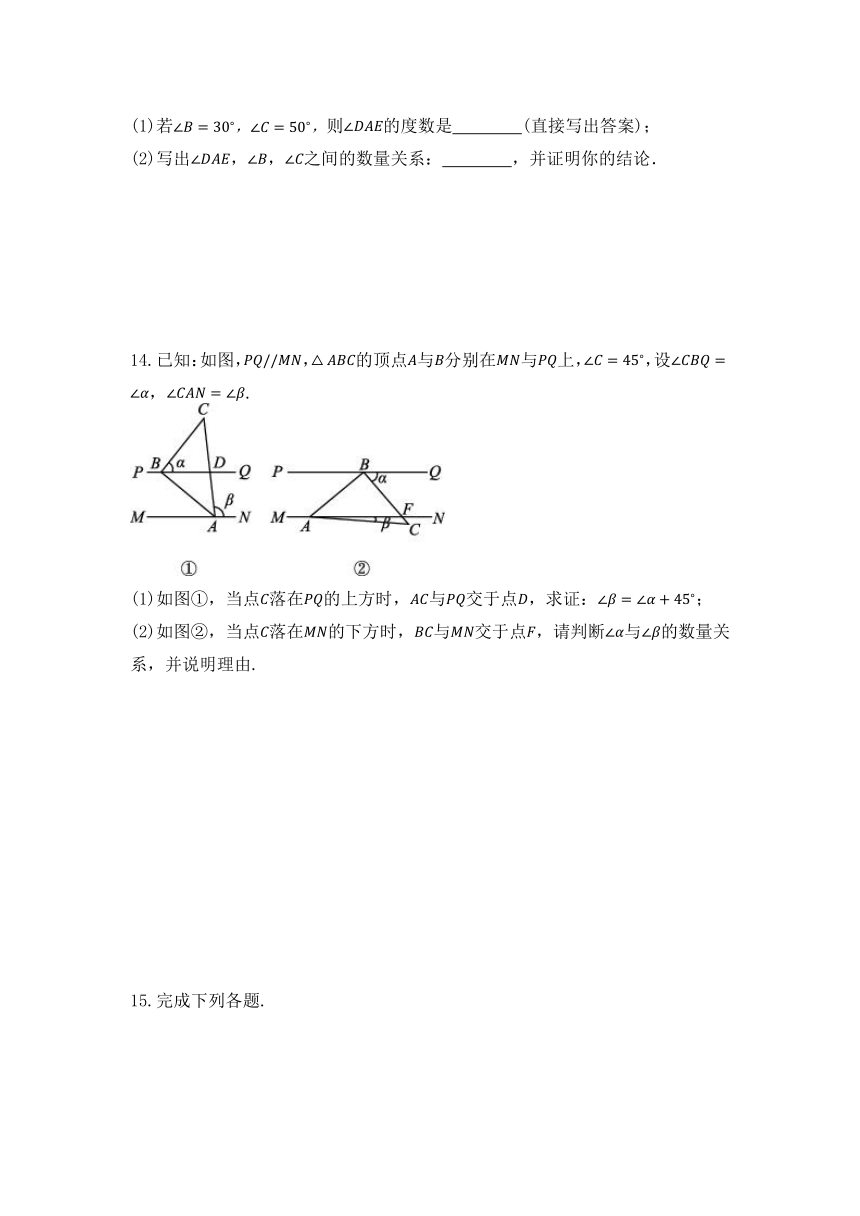

文档简介
12.2第三课时:与三角形内角和有关的证明
1.如图,在中,,,,的度数是( )
A. B. C. D.
2.如图,点在的边的延长线上,,则下列结论正确的是( )
A. B.
C. D.
3.如图在中,,点在上,将沿折叠,点恰好落在边上的点处,若,则的度数为( )
A. B. C. D.
4.如图,, 点,分别在,的延长线上,
,,分别平分,,.
有以下结论:①;②;③平分;
④;⑤.
其中正确的结论有( )
A.个 B.个 C.个 D.个
5.如图,在中,点,分别在,边上比较大小: 填“ ”,“ ”或“ ”
6.如图,直线,,,互不平行,以下结论正确的是 (只填序号).
①;②;
③;④
7.请把下面的解题过程补充完整.
如图,是的一个外角,那么它与不相邻的两个内角,之间有怎样的数量关系?为什么?
解: .
理由: ),
(邻补角的定义),
(等量代换)
8.在中,,,点在边上,连接,若为直角三角形,则的度数为 .
9.如图,已知于点,交于点,且,,则 °.
三、解答题(共6小题)
10.已知:如图,中,,于,求证:.
11.如图,是的外角的平分线,且交的延长线于点.
(1)若,,求的度数;
(2)请你写出、、三个角之间存在的等量关系,并写出证明过程.
12.如图,在中,,平分交于点,为线段(端点除外)上的一个动点,交直线于点.
(1)若,,求的度数;
(2)当点在线段上运动时,求证:
13.已知:如图,在中,,,分别是的高和角平分线.
(1)若则的度数是 (直接写出答案);
(2)写出,,之间的数量关系: ,并证明你的结论.
14.已知:如图,,的顶点与分别在与上,,设,.
(1)如图①,当点落在的上方时,与交于点,求证:;
(2)如图②,当点落在的下方时,与交于点,请判断与的数量关系,并说明理由.
15.完成下列各题.
(1)如图,,的顶点重合,且,则 (直接写出结果).
(2)连接,,若,,,分别是四边形的四个内角的平分线.
①如图,如果,那么的度数为 (直接写出结果);
②如图,若,则与平行吗?为什么?
参考答案
1.
【答案】:B
【解析】: ,
,
,
.
故选:
2.
【答案】:C
【解析】:
故选:
3.
【答案】:C
【解析】:,
.
是由翻折得到的,
.
,
,
,
解得.
故选:
4.
【答案】:D
【解析】:平分
①正确;
平分
②正确;
与不一定相等
与不一定相等
平分不一定成立
③错误;
平分
平分
④正确;
⑤正确.
故选
5.
【答案】:
【解析】:,,
,,
故答案为:
6.
【答案】:①②③
【解析】:由三角形外角的性质可知:,,,
故①②③正确.
故答案为:①②③
7.
【答案】:;;三角形内角和定理
;
8.
【答案】:或
【解析】:分两种情况:
①如图,
当时,
,
;
②如图,
当时,
,,
,
.
综上,的度数为或.
故答案为或.
9.
【答案】:
【解析】:于点
10.
【答案】:证明:,
.
【解析】:由三角形的内角和定理可求,由直角三角形的性质可得,即可得结论.
11
(1)解:,,
,
平分,
,
.
(2),证明如下:
, ,
.
12
(1)解:,平分
(2)证明:平分即
13
(1)
【解析】:,是的角平分线是的高故答案为.
(2)解:证明:是的高是的角平分线
14
(1)证明:是的一个外角
(2)解:理由如下:是的一个外角
15
(1)
【解析】:.故答案为.
(2)①,,,分别是四边形的四个内角的平分线,,,,,.在四边形中,.在中,在中,,..故答案为.②.理由如下:,,,分别是四边形的四个内角的平分线,,,,,.在四边形中.在中在中..在中.,
1.如图,在中,,,,的度数是( )
A. B. C. D.
2.如图,点在的边的延长线上,,则下列结论正确的是( )
A. B.
C. D.
3.如图在中,,点在上,将沿折叠,点恰好落在边上的点处,若,则的度数为( )
A. B. C. D.
4.如图,, 点,分别在,的延长线上,
,,分别平分,,.
有以下结论:①;②;③平分;
④;⑤.
其中正确的结论有( )
A.个 B.个 C.个 D.个
5.如图,在中,点,分别在,边上比较大小: 填“ ”,“ ”或“ ”
6.如图,直线,,,互不平行,以下结论正确的是 (只填序号).
①;②;
③;④
7.请把下面的解题过程补充完整.
如图,是的一个外角,那么它与不相邻的两个内角,之间有怎样的数量关系?为什么?
解: .
理由: ),
(邻补角的定义),
(等量代换)
8.在中,,,点在边上,连接,若为直角三角形,则的度数为 .
9.如图,已知于点,交于点,且,,则 °.
三、解答题(共6小题)
10.已知:如图,中,,于,求证:.
11.如图,是的外角的平分线,且交的延长线于点.
(1)若,,求的度数;
(2)请你写出、、三个角之间存在的等量关系,并写出证明过程.
12.如图,在中,,平分交于点,为线段(端点除外)上的一个动点,交直线于点.
(1)若,,求的度数;
(2)当点在线段上运动时,求证:
13.已知:如图,在中,,,分别是的高和角平分线.
(1)若则的度数是 (直接写出答案);
(2)写出,,之间的数量关系: ,并证明你的结论.
14.已知:如图,,的顶点与分别在与上,,设,.
(1)如图①,当点落在的上方时,与交于点,求证:;
(2)如图②,当点落在的下方时,与交于点,请判断与的数量关系,并说明理由.
15.完成下列各题.
(1)如图,,的顶点重合,且,则 (直接写出结果).
(2)连接,,若,,,分别是四边形的四个内角的平分线.
①如图,如果,那么的度数为 (直接写出结果);
②如图,若,则与平行吗?为什么?
参考答案
1.
【答案】:B
【解析】: ,
,
,
.
故选:
2.
【答案】:C
【解析】:
故选:
3.
【答案】:C
【解析】:,
.
是由翻折得到的,
.
,
,
,
解得.
故选:
4.
【答案】:D
【解析】:平分
①正确;
平分
②正确;
与不一定相等
与不一定相等
平分不一定成立
③错误;
平分
平分
④正确;
⑤正确.
故选
5.
【答案】:
【解析】:,,
,,
故答案为:
6.
【答案】:①②③
【解析】:由三角形外角的性质可知:,,,
故①②③正确.
故答案为:①②③
7.
【答案】:;;三角形内角和定理
;
8.
【答案】:或
【解析】:分两种情况:
①如图,
当时,
,
;
②如图,
当时,
,,
,
.
综上,的度数为或.
故答案为或.
9.
【答案】:
【解析】:于点
10.
【答案】:证明:,
.
【解析】:由三角形的内角和定理可求,由直角三角形的性质可得,即可得结论.
11
(1)解:,,
,
平分,
,
.
(2),证明如下:
, ,
.
12
(1)解:,平分
(2)证明:平分即
13
(1)
【解析】:,是的角平分线是的高故答案为.
(2)解:证明:是的高是的角平分线
14
(1)证明:是的一个外角
(2)解:理由如下:是的一个外角
15
(1)
【解析】:.故答案为.
(2)①,,,分别是四边形的四个内角的平分线,,,,,.在四边形中,.在中,在中,,..故答案为.②.理由如下:,,,分别是四边形的四个内角的平分线,,,,,.在四边形中.在中在中..在中.,
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
