17.1勾股定理 同步练习(含答案) 2022-2023学年八年级数学下册人教版
文档属性
| 名称 | 17.1勾股定理 同步练习(含答案) 2022-2023学年八年级数学下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 380.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-03 15:29:48 | ||
图片预览



文档简介
17.1勾股定理
(同步练习)
一、单选题
1.如图,三角形纸片ABC中,点D是BC边上一点,连接AD,把△ABD沿着直线AD翻折,得到△AED,DE交AC于点G,连接BE交AD于点F.若DG=EG,AF=4,AB=5,△AEG的面积为,则的值为( )
A.13 B.12 C.11 D.10
2.观察“赵爽弦图”(如图),若图中四个全等的直角三角形的两直角边分别为a,b,,根据图中图形面积之间的关系及勾股定理,可直接得到等式( )
A. B.
C. D.
3.如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是( )
A.厘米 B.10厘米 C.厘米 D.8厘米
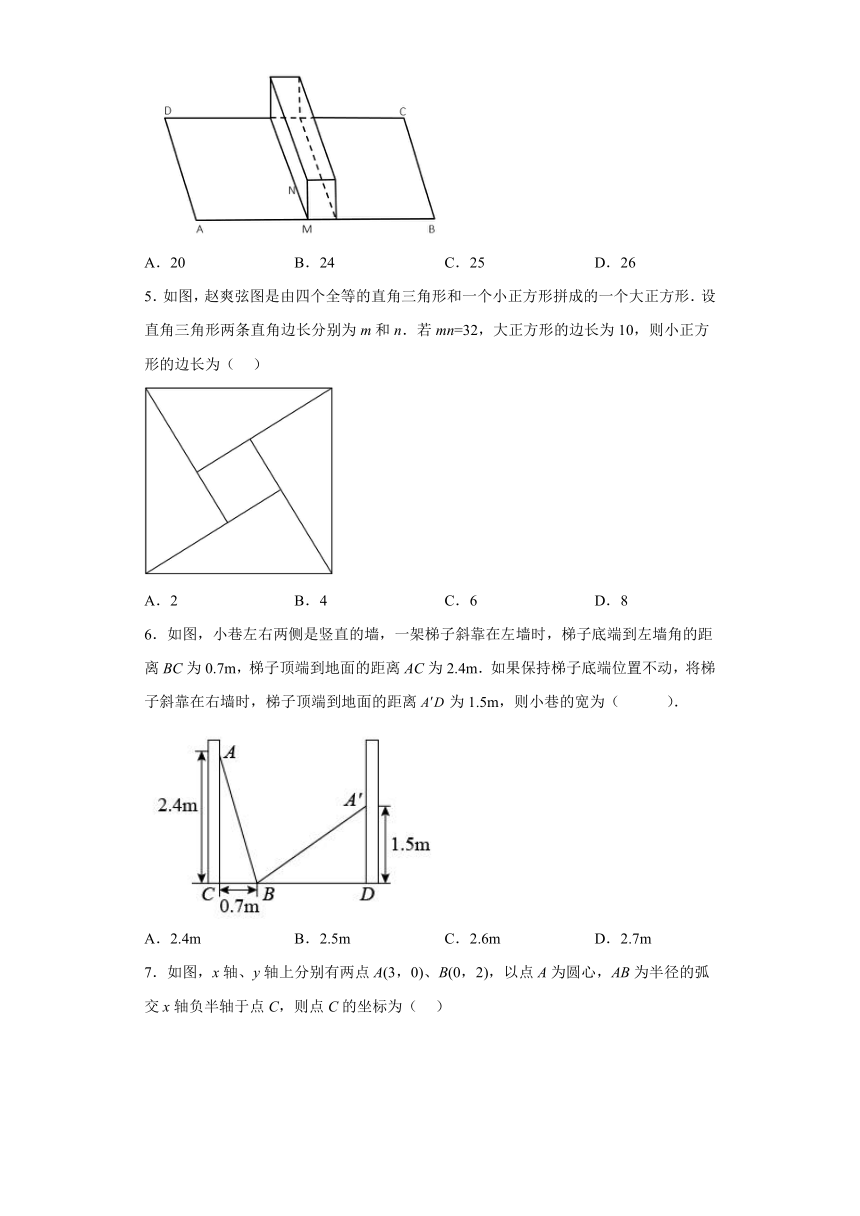
4.如图所示,是长方形地面,长,宽,中间整有一堵砖墙高,一只蚂蚁从A点爬到C点,它必须翻过中间那堵墙,则它至少要走( )
A.20 B.24 C.25 D.26
5.如图,赵爽弦图是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形两条直角边长分别为m和n.若mn=32,大正方形的边长为10,则小正方形的边长为( )
A.2 B.4 C.6 D.8
6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7m,梯子顶端到地面的距离AC为2.4m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为1.5m,则小巷的宽为( ).
A.2.4m B.2.5m C.2.6m D.2.7m
7.如图,x轴、y轴上分别有两点A(3,0)、B(0,2),以点A为圆心,AB为半径的弧交x轴负半轴于点C,则点C的坐标为( )
A.(﹣1,0) B.(2,0) C.(3,0) D.(3,0)
8.在△ABC中,∠C=90°,AB=3,则的值为( )
A.24 B.18 C.12 D.9
9.的半径为,弦.若,则和的距离为( )
A. B. C.或 D.或
10.如图,已知OA=OB,点A表示的数为a,则下列说法正确的是( )
A.a的值为 B.a的值为
C.a的相反数为 D.a的倒数为
二、填空题
11.如图,Rt△ABC中,∠ACB=90°,AC=2,BC=4,CD是△ABC的中线,E是边BC上一动点,将△BED沿ED折叠,点B落在点F处,EF交线段CD于点G,当△DFG是直角三角形时,则CE=__________.
12.课本中有这样一句话:“利用勾股定理可以作出,,…线段(如图所示).”即:,过A作且,根据勾股定理,得;再过作且,得;…以此类推,得________.
13.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则这最大的直角三角形的面积是______.
14.我国古代数学名著《算法统宗)有一道“荡秋干”的问题,“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:如图,有一架秋千,当它静止时,踏板离地距离PA的长为1尺,将它向前水平推送10尺时,即尺,秋千踏板离地的距离就和身高5尺的人一样高,秋千的绳索始终拉得很直,则秋千的绳索长为________尺.
15.如图,分别以此直角三角形的三边为直径在三角形外部画半圆,若S1=9π,S2=16π,则S3=_____.
三、解答题
16.如图所示,一架云梯长25m,斜靠在一面墙上,梯子底端离墙7m,这个梯子的顶端距地面有多高?如果梯子顶端下滑了4m,那么梯子的底端在水平方向上也滑动了4m吗?
17.如图所示,长方形纸片ABCD的长AD=8cm,宽AB=4cm,将其沿着折痕EF折叠,使点D与点B重合.
(1)求证:BE=BF;
(2)求折叠后△BEF的面积.
18.小明将一副三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其他各边的长.若已知CD=,求AB的长.
19.我们知道,到线段两端距离相等的点在线段的垂直平分线上.由此,我们可以引入如下新定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
(1)如图1,点P在线段BC上,∠ABP=∠APD=∠PCD=90°,BP=CD.求证:点P是△APD的准外心;
(2)如图2,在Rt△ABC中,∠BAC=90°,BC=5,AB=3,△ABC的准外心P在△ABC的直角边上,试求AP的长.
20.如图,,,.
(1)求证:≌.
(2)若,,,求的长.
21.小王与小林进行遥控赛车游戏,终点为点,小王的赛车从点出发,以米/秒的速度由西向东行驶,同时小林的赛车从点出发,以米/秒的速度由南向北行驶(如图).已知赛车之间的距离小于或等于米时,遥控信号会产生相互干扰,米,米,
(1)出发秒钟时,遥控信号是否会产生相互干扰?
(2)当两赛车距点的距离之和为米时,遥控信号是否会产生相互干扰?
参考答案:
1.A2.C3.B4.D5.C6.D7.D8.B9.C10.C
11.1或
12.
13.
14.14.5
15.
16.这个梯子的顶端距地面24m;梯子的底端在水平方向上不是滑动了4m,而是滑动了8m.
17.(1)由折叠的性质得:∠BEF=∠DEF,
∵ADBC,
∴∠BFE=∠DEF,
∴∠BFE=∠BEF,
∴BE=BF;
(2)设AE=x,则BE=DE=8﹣x,
在Rt△ABE中,由勾股定理得:x2+42=(8﹣x)2
解得,x=3,
∴BE=BF=5,
∴△BEF的面积=×BF×AB=×5×4=10.
18..
19.(1)证明:∵∠ABP=∠APD=∠PCD=90°,
∴∠APB+∠PAB=90°,∠APB+∠DPC=90°,
∴∠PAB=∠DPC,
在△ABP和△PCD中,
,
∴△ABP≌△PCD(AAS),
∴AP=PD,
∴点P是△APD的准外心;
(2)解:∵∠BAC=90°,BC=5,AB=3,
∴AC4,
当P点在AB上,PA=PB,则APAB;
当P点在AC上,PA=PC,则APAC=2,
当P点在AC上,PB=PC,如图2,
设AP=t,则PC=PB=4﹣x,
在Rt△ABP中,32+t2=(4﹣t)2,解得t,
即此时AP,
综上所述,AP的长为或2或.
20.(1)证明:∵,
∴,
∴.
在与中,
,
∴≌;
(2)解:∵≌,
∴,
∵,,
∴.
21.(1)出发三秒钟时,遥控信号不会产生相互干扰;(2)当两赛车的距离之和为米时,遥控信号将会产生干扰.
(同步练习)
一、单选题
1.如图,三角形纸片ABC中,点D是BC边上一点,连接AD,把△ABD沿着直线AD翻折,得到△AED,DE交AC于点G,连接BE交AD于点F.若DG=EG,AF=4,AB=5,△AEG的面积为,则的值为( )
A.13 B.12 C.11 D.10
2.观察“赵爽弦图”(如图),若图中四个全等的直角三角形的两直角边分别为a,b,,根据图中图形面积之间的关系及勾股定理,可直接得到等式( )
A. B.
C. D.
3.如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是( )
A.厘米 B.10厘米 C.厘米 D.8厘米
4.如图所示,是长方形地面,长,宽,中间整有一堵砖墙高,一只蚂蚁从A点爬到C点,它必须翻过中间那堵墙,则它至少要走( )
A.20 B.24 C.25 D.26
5.如图,赵爽弦图是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形两条直角边长分别为m和n.若mn=32,大正方形的边长为10,则小正方形的边长为( )
A.2 B.4 C.6 D.8
6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7m,梯子顶端到地面的距离AC为2.4m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为1.5m,则小巷的宽为( ).
A.2.4m B.2.5m C.2.6m D.2.7m
7.如图,x轴、y轴上分别有两点A(3,0)、B(0,2),以点A为圆心,AB为半径的弧交x轴负半轴于点C,则点C的坐标为( )
A.(﹣1,0) B.(2,0) C.(3,0) D.(3,0)
8.在△ABC中,∠C=90°,AB=3,则的值为( )
A.24 B.18 C.12 D.9
9.的半径为,弦.若,则和的距离为( )
A. B. C.或 D.或
10.如图,已知OA=OB,点A表示的数为a,则下列说法正确的是( )
A.a的值为 B.a的值为
C.a的相反数为 D.a的倒数为
二、填空题
11.如图,Rt△ABC中,∠ACB=90°,AC=2,BC=4,CD是△ABC的中线,E是边BC上一动点,将△BED沿ED折叠,点B落在点F处,EF交线段CD于点G,当△DFG是直角三角形时,则CE=__________.
12.课本中有这样一句话:“利用勾股定理可以作出,,…线段(如图所示).”即:,过A作且,根据勾股定理,得;再过作且,得;…以此类推,得________.
13.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则这最大的直角三角形的面积是______.
14.我国古代数学名著《算法统宗)有一道“荡秋干”的问题,“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:如图,有一架秋千,当它静止时,踏板离地距离PA的长为1尺,将它向前水平推送10尺时,即尺,秋千踏板离地的距离就和身高5尺的人一样高,秋千的绳索始终拉得很直,则秋千的绳索长为________尺.
15.如图,分别以此直角三角形的三边为直径在三角形外部画半圆,若S1=9π,S2=16π,则S3=_____.
三、解答题
16.如图所示,一架云梯长25m,斜靠在一面墙上,梯子底端离墙7m,这个梯子的顶端距地面有多高?如果梯子顶端下滑了4m,那么梯子的底端在水平方向上也滑动了4m吗?
17.如图所示,长方形纸片ABCD的长AD=8cm,宽AB=4cm,将其沿着折痕EF折叠,使点D与点B重合.
(1)求证:BE=BF;
(2)求折叠后△BEF的面积.
18.小明将一副三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其他各边的长.若已知CD=,求AB的长.
19.我们知道,到线段两端距离相等的点在线段的垂直平分线上.由此,我们可以引入如下新定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
(1)如图1,点P在线段BC上,∠ABP=∠APD=∠PCD=90°,BP=CD.求证:点P是△APD的准外心;
(2)如图2,在Rt△ABC中,∠BAC=90°,BC=5,AB=3,△ABC的准外心P在△ABC的直角边上,试求AP的长.
20.如图,,,.
(1)求证:≌.
(2)若,,,求的长.
21.小王与小林进行遥控赛车游戏,终点为点,小王的赛车从点出发,以米/秒的速度由西向东行驶,同时小林的赛车从点出发,以米/秒的速度由南向北行驶(如图).已知赛车之间的距离小于或等于米时,遥控信号会产生相互干扰,米,米,
(1)出发秒钟时,遥控信号是否会产生相互干扰?
(2)当两赛车距点的距离之和为米时,遥控信号是否会产生相互干扰?
参考答案:
1.A2.C3.B4.D5.C6.D7.D8.B9.C10.C
11.1或
12.
13.
14.14.5
15.
16.这个梯子的顶端距地面24m;梯子的底端在水平方向上不是滑动了4m,而是滑动了8m.
17.(1)由折叠的性质得:∠BEF=∠DEF,
∵ADBC,
∴∠BFE=∠DEF,
∴∠BFE=∠BEF,
∴BE=BF;
(2)设AE=x,则BE=DE=8﹣x,
在Rt△ABE中,由勾股定理得:x2+42=(8﹣x)2
解得,x=3,
∴BE=BF=5,
∴△BEF的面积=×BF×AB=×5×4=10.
18..
19.(1)证明:∵∠ABP=∠APD=∠PCD=90°,
∴∠APB+∠PAB=90°,∠APB+∠DPC=90°,
∴∠PAB=∠DPC,
在△ABP和△PCD中,
,
∴△ABP≌△PCD(AAS),
∴AP=PD,
∴点P是△APD的准外心;
(2)解:∵∠BAC=90°,BC=5,AB=3,
∴AC4,
当P点在AB上,PA=PB,则APAB;
当P点在AC上,PA=PC,则APAC=2,
当P点在AC上,PB=PC,如图2,
设AP=t,则PC=PB=4﹣x,
在Rt△ABP中,32+t2=(4﹣t)2,解得t,
即此时AP,
综上所述,AP的长为或2或.
20.(1)证明:∵,
∴,
∴.
在与中,
,
∴≌;
(2)解:∵≌,
∴,
∵,,
∴.
21.(1)出发三秒钟时,遥控信号不会产生相互干扰;(2)当两赛车的距离之和为米时,遥控信号将会产生干扰.
