8.2重力势能 课件(共22张PPT)
文档属性
| 名称 | 8.2重力势能 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-03 10:37:50 | ||
图片预览







文档简介
(共22张PPT)
第2节 重力势能
年 级:高一
学 科:物理(人教版)
物体因为处于一定的高度而具有的能量称为重力势能。
一、重力势能
重力势能与物体的质量(m)和所处的高度(h)有关。
当物体的高度发生变化时,重力做功,势能发生变化:物体下降时重力做正功,势能减小;物体被举高时重力做负功,势能增大。因此,重力势能与重力做功密切相关。
WG = mgΔh
= mgh1-mgh2
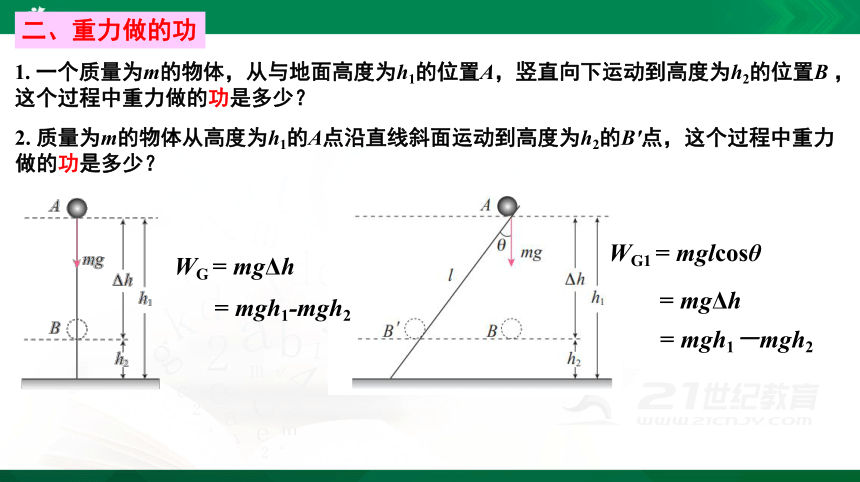
1. 一个质量为m的物体,从与地面高度为h1的位置A,竖直向下运动到高度为h2的位置B ,这个过程中重力做的功是多少?
二、重力做的功
2. 质量为m的物体从高度为h1的A点沿直线斜面运动到高度为h2的B′点,这个过程中重力做的功是多少?
= mgh1-mgh2
WG1 = mglcosθ
= mgΔh
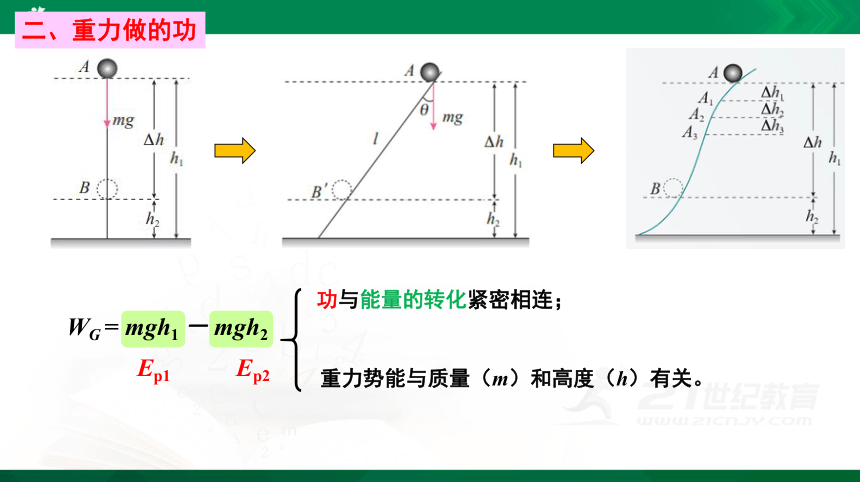
微元法
WG = mg h1+mg h2+mg h3+…
= mgh1-mgh2
= mgΔh
3. 质量为m的物体从高度为h1处的A点沿曲线运动到高度为h2的B点,则:重力所做的功是否还一样呢?
二、重力做的功
重力做功的特点:
物体运动时,重力对它做的功只跟它的起点和终点的位置有关,而跟物体运动的路径无关。
二、重力做的功
重力势能与质量(m)和高度(h)有关。
功与能量的转化紧密相连;
WG = mgh1 - mgh2
Ep1
Ep2
二、重力做的功
4. 重力势能是地球和物体组成的系统所共有的。
1. 定义:物体的重力势能等于它所受的重力与所处高度的乘积;
2. 表达式: EP=mgh
3. 国际单位:
焦耳(J)
1J=1kg·m·s-2·m=1N·m
三、重力势能(EP)
物体的重力势能总是相对于某一水平面来说,这个水平面叫做参考平面,又叫做零势能面。在这个水平面上,物体的重力势能取为零。
O
O
O
重力势能是标量,但有正负,且正负表示大小。
(1)若物体在参考面,h=0,故Ep=0 ;
三、重力势能(EP)
重力势能具有相对性
(2)若物体在参考面上方,则 h>0为正值,Ep也是正值;
(3)若物体在参考面下方,则 h<0为负值,Ep也是负值;
1到2阶段:重力做负功
WG= -mgh,重力势能增加了mgh
WG=EP1 - EP2 = -△Ep
2到3阶段:重力做正功
WG= mgh,重力势能减小了mgh
重力做的功等于重力势能的减少量。
三、重力势能(EP)
重力做功与重力势能
例1. 质量为m的小球从距离地面高为h处由静止下落,碰地后弹起的高度为 h,然后下落,又弹起高度为 h,已知重力加速度为g,空气阻力大小始终为f,在此过程中,求:
①空气阻力对小球做的功?
②重力对小球做的功?
三、重力势能(EP)
重力做功与重力势能
① 空气阻力做功为Wf = - f (h+0.5h+0.5h+0.25h)= - 2.25 f h
②重力做功与路径无关,只与初末位置有关,WG = mg(h-0.25h)=0.75mgh
例2. 如图在光滑的桌面上有一根均匀柔软的绳子,质量为m,长度为L,绳子的 悬于桌面以下。则从绳子开始下滑至刚好全部离开桌面的过程中,绳子的重力势能减小了多少?(重力加速度为g,桌面离地足够高)
① 选择桌面为参考平面:
三、重力势能(EP)
重力做功与重力势能
末态:Ep2=(mg)× (-L/2) = -mgL/2
初态:Ep1=0+ (0.25mg)×(-L/8) = - mgL/32
重力势能减少量为:Ep1-Ep2=-15mgL/32
例2. 如图,在光滑的桌面上有一根均匀柔软的绳子,质量为m,长度为L,绳子的 悬于桌面以下。则从绳子开始下滑至刚好全部离开桌面的过程中,绳子的重力势能减小了多少?(重力加速度为g,桌面离地足够高)
可看作右侧0.25L不变,重力对左侧0.75L做功为:
三、重力势能(EP)
重力做功与重力势能
② 运用割补法求解:
重力势能减少量为:-ΔEp=WG=15mgL/32
WG = (0.75mg)×(3L/8+L/4) =15mgL/32
四、弹性势能(EP)
拉长或压缩的弹簧、卷紧的发条、拉开的弓、正在击球的网球拍、撑竿跳高运动员手中弯曲的竿等,这些物体都发生了弹性形变,每个物体的各部分之间都有弹力的相互作用。发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫作弹性势能。
四、弹性势能(EP)
1. 弹性势能与形变的大小有关系。例如,在弹性限度内,弹簧的弹性势能跟弹簧被拉伸或压缩的长度有关。被拉伸或压缩的长度越长,恢复原状过程中对外做的功就越多,弹簧的弹性势能就越大。
四、弹性势能(EP)
2. 弹簧的弹性势能还与弹簧的劲度系数有关。不同的弹簧发生同样大小的形变,劲度系数越大,弹簧恢复原状过程中对外做的功就越多,因而弹簧的弹性势能就越大。
1. 定义:发生弹性形变的物体各部分之间由于弹力的相互作用而具有的势能。
2. 影响因素:
(1)弹簧形变量
(2)弹簧劲度系数
四、弹性势能(EP)
势能也叫位能,与相互作用的物体的相对位置有关。
重力势能是由地球和地面上物体的相对位置决定的;
弹性势能是由发生弹性形变的物体各部分的相对位置决定的。
WG = -△EP = EP1 - EP2
W弹 = -△EP = EP1 - EP2
o
x
F
w弹
四、弹性势能(EP)
W弹 = F △x = S阴影
x
kx
3. 表达式:
光滑地面上,用外力F缓慢向右拉动物块,物块缓慢拉动弹簧。
弹簧弹力时刻与外力等大反向:F=kx
微元法
S阴影
= 1/2 x kx = 1/2 kx
2
W弹 = -△EP = EP1 - EP2
五、练习与应用
1. 图中的几个斜面,它们的高度相同、倾角不同。让质量相同的物体沿斜面从顶端运动到底端。试根据功的定义计算沿不同斜面运动时重力做的功,它的大小与斜面的倾角是否有关?
解:
沿不同斜面运动时重力做的功大小相等,与斜面的倾斜角度无关。
五、练习与应用
2. 质量为m的足球在地面1的位置被踢出后落到地面3位置,在空中达到的最高点2的高度为h。重力加速度为g。
(1)足球由位置1运动到位置2时,重力做了多少功?足球的重力势能增加了多少?
(2)足球由位置2运动到位置3时,重力做了多少功?足球的重力势能减少了多少?
解:
(1)
(2)
五、练习与应用
3. 以下说法是否正确?如果正确,说出一种可能的实际情况;如果不正确,说明这种说法为什么错误。
(1)物体受拉力作用向上运动,拉力做的功是1J,但物体重力势能的增加量不是1J;
(2)物体受拉力作用向上匀速运动,拉力做的功是1J,但物体重力势能的增加量不是1J;
(1)正确。物体在拉力的作用下向上运动,如果做匀加速直线运动,这时拉力的功大于重力势能的增加量。如果物体做匀减速直线运动,这时拉力的功小于重力势能的增加量。
(2)错误。物体匀速上升,拉力的大小等于重力的大小,拉力的功一定等于重力势能的增加量。
解:
五、练习与应用
3. 以下说法是否正确?如果正确,说出一种可能的实际情况;如果不正确,说明这种说法为什么错误。
(3)物体运动,重力做的功是-1J,但物体重力势能的增加量不是1J;
(4)没有摩擦时物体由A沿直线运动到B,重力做的功是-1J;有摩擦时物体由A沿曲线运动到B,重力做的功大于-1J。
(3)错误。根据WG= Ep1 –Ep2可知,重力做-1J的功,物体重力势能的增加量为1J。
(4)错误。重力做功只与起点和终点的位置有关,与路径无关,A、B两点的位置不变,从A点到B点的过程中,无论经过什么路径,是否还受到其他的力,重力的功都是相同的。
解:
五、练习与应用
4. 质量m=0.5 kg的小球,从桌面上方高h1= 1.2 m的A点下落到地面上的B点,桌面离地面的高度h2 = 0.8 m。试完成下面的表格。 (g取10 m/s2)
所选择的参考平面 小球在A点 的重力势能 小球在B点的重力势能 整个下落过程中小球重力做的功 整个下落过程中小球重力势能的变化量
桌面
地面
6 J
10 J
-4 J
0
10 J
10 J
减少10 J
减少10 J
重力势能具有相对性,重力势能的变化量具有绝对性。
(1)在表格的空白处按要求填入数据。
(2)如果下落时有空气阻力,表中的数据是否会改变?
解:
如果下落时有空气阻力,表中的数据不会改变。
第2节 重力势能
年 级:高一
学 科:物理(人教版)
物体因为处于一定的高度而具有的能量称为重力势能。
一、重力势能
重力势能与物体的质量(m)和所处的高度(h)有关。
当物体的高度发生变化时,重力做功,势能发生变化:物体下降时重力做正功,势能减小;物体被举高时重力做负功,势能增大。因此,重力势能与重力做功密切相关。
WG = mgΔh
= mgh1-mgh2
1. 一个质量为m的物体,从与地面高度为h1的位置A,竖直向下运动到高度为h2的位置B ,这个过程中重力做的功是多少?
二、重力做的功
2. 质量为m的物体从高度为h1的A点沿直线斜面运动到高度为h2的B′点,这个过程中重力做的功是多少?
= mgh1-mgh2
WG1 = mglcosθ
= mgΔh
微元法
WG = mg h1+mg h2+mg h3+…
= mgh1-mgh2
= mgΔh
3. 质量为m的物体从高度为h1处的A点沿曲线运动到高度为h2的B点,则:重力所做的功是否还一样呢?
二、重力做的功
重力做功的特点:
物体运动时,重力对它做的功只跟它的起点和终点的位置有关,而跟物体运动的路径无关。
二、重力做的功
重力势能与质量(m)和高度(h)有关。
功与能量的转化紧密相连;
WG = mgh1 - mgh2
Ep1
Ep2
二、重力做的功
4. 重力势能是地球和物体组成的系统所共有的。
1. 定义:物体的重力势能等于它所受的重力与所处高度的乘积;
2. 表达式: EP=mgh
3. 国际单位:
焦耳(J)
1J=1kg·m·s-2·m=1N·m
三、重力势能(EP)
物体的重力势能总是相对于某一水平面来说,这个水平面叫做参考平面,又叫做零势能面。在这个水平面上,物体的重力势能取为零。
O
O
O
重力势能是标量,但有正负,且正负表示大小。
(1)若物体在参考面,h=0,故Ep=0 ;
三、重力势能(EP)
重力势能具有相对性
(2)若物体在参考面上方,则 h>0为正值,Ep也是正值;
(3)若物体在参考面下方,则 h<0为负值,Ep也是负值;
1到2阶段:重力做负功
WG= -mgh,重力势能增加了mgh
WG=EP1 - EP2 = -△Ep
2到3阶段:重力做正功
WG= mgh,重力势能减小了mgh
重力做的功等于重力势能的减少量。
三、重力势能(EP)
重力做功与重力势能
例1. 质量为m的小球从距离地面高为h处由静止下落,碰地后弹起的高度为 h,然后下落,又弹起高度为 h,已知重力加速度为g,空气阻力大小始终为f,在此过程中,求:
①空气阻力对小球做的功?
②重力对小球做的功?
三、重力势能(EP)
重力做功与重力势能
① 空气阻力做功为Wf = - f (h+0.5h+0.5h+0.25h)= - 2.25 f h
②重力做功与路径无关,只与初末位置有关,WG = mg(h-0.25h)=0.75mgh
例2. 如图在光滑的桌面上有一根均匀柔软的绳子,质量为m,长度为L,绳子的 悬于桌面以下。则从绳子开始下滑至刚好全部离开桌面的过程中,绳子的重力势能减小了多少?(重力加速度为g,桌面离地足够高)
① 选择桌面为参考平面:
三、重力势能(EP)
重力做功与重力势能
末态:Ep2=(mg)× (-L/2) = -mgL/2
初态:Ep1=0+ (0.25mg)×(-L/8) = - mgL/32
重力势能减少量为:Ep1-Ep2=-15mgL/32
例2. 如图,在光滑的桌面上有一根均匀柔软的绳子,质量为m,长度为L,绳子的 悬于桌面以下。则从绳子开始下滑至刚好全部离开桌面的过程中,绳子的重力势能减小了多少?(重力加速度为g,桌面离地足够高)
可看作右侧0.25L不变,重力对左侧0.75L做功为:
三、重力势能(EP)
重力做功与重力势能
② 运用割补法求解:
重力势能减少量为:-ΔEp=WG=15mgL/32
WG = (0.75mg)×(3L/8+L/4) =15mgL/32
四、弹性势能(EP)
拉长或压缩的弹簧、卷紧的发条、拉开的弓、正在击球的网球拍、撑竿跳高运动员手中弯曲的竿等,这些物体都发生了弹性形变,每个物体的各部分之间都有弹力的相互作用。发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫作弹性势能。
四、弹性势能(EP)
1. 弹性势能与形变的大小有关系。例如,在弹性限度内,弹簧的弹性势能跟弹簧被拉伸或压缩的长度有关。被拉伸或压缩的长度越长,恢复原状过程中对外做的功就越多,弹簧的弹性势能就越大。
四、弹性势能(EP)
2. 弹簧的弹性势能还与弹簧的劲度系数有关。不同的弹簧发生同样大小的形变,劲度系数越大,弹簧恢复原状过程中对外做的功就越多,因而弹簧的弹性势能就越大。
1. 定义:发生弹性形变的物体各部分之间由于弹力的相互作用而具有的势能。
2. 影响因素:
(1)弹簧形变量
(2)弹簧劲度系数
四、弹性势能(EP)
势能也叫位能,与相互作用的物体的相对位置有关。
重力势能是由地球和地面上物体的相对位置决定的;
弹性势能是由发生弹性形变的物体各部分的相对位置决定的。
WG = -△EP = EP1 - EP2
W弹 = -△EP = EP1 - EP2
o
x
F
w弹
四、弹性势能(EP)
W弹 = F △x = S阴影
x
kx
3. 表达式:
光滑地面上,用外力F缓慢向右拉动物块,物块缓慢拉动弹簧。
弹簧弹力时刻与外力等大反向:F=kx
微元法
S阴影
= 1/2 x kx = 1/2 kx
2
W弹 = -△EP = EP1 - EP2
五、练习与应用
1. 图中的几个斜面,它们的高度相同、倾角不同。让质量相同的物体沿斜面从顶端运动到底端。试根据功的定义计算沿不同斜面运动时重力做的功,它的大小与斜面的倾角是否有关?
解:
沿不同斜面运动时重力做的功大小相等,与斜面的倾斜角度无关。
五、练习与应用
2. 质量为m的足球在地面1的位置被踢出后落到地面3位置,在空中达到的最高点2的高度为h。重力加速度为g。
(1)足球由位置1运动到位置2时,重力做了多少功?足球的重力势能增加了多少?
(2)足球由位置2运动到位置3时,重力做了多少功?足球的重力势能减少了多少?
解:
(1)
(2)
五、练习与应用
3. 以下说法是否正确?如果正确,说出一种可能的实际情况;如果不正确,说明这种说法为什么错误。
(1)物体受拉力作用向上运动,拉力做的功是1J,但物体重力势能的增加量不是1J;
(2)物体受拉力作用向上匀速运动,拉力做的功是1J,但物体重力势能的增加量不是1J;
(1)正确。物体在拉力的作用下向上运动,如果做匀加速直线运动,这时拉力的功大于重力势能的增加量。如果物体做匀减速直线运动,这时拉力的功小于重力势能的增加量。
(2)错误。物体匀速上升,拉力的大小等于重力的大小,拉力的功一定等于重力势能的增加量。
解:
五、练习与应用
3. 以下说法是否正确?如果正确,说出一种可能的实际情况;如果不正确,说明这种说法为什么错误。
(3)物体运动,重力做的功是-1J,但物体重力势能的增加量不是1J;
(4)没有摩擦时物体由A沿直线运动到B,重力做的功是-1J;有摩擦时物体由A沿曲线运动到B,重力做的功大于-1J。
(3)错误。根据WG= Ep1 –Ep2可知,重力做-1J的功,物体重力势能的增加量为1J。
(4)错误。重力做功只与起点和终点的位置有关,与路径无关,A、B两点的位置不变,从A点到B点的过程中,无论经过什么路径,是否还受到其他的力,重力的功都是相同的。
解:
五、练习与应用
4. 质量m=0.5 kg的小球,从桌面上方高h1= 1.2 m的A点下落到地面上的B点,桌面离地面的高度h2 = 0.8 m。试完成下面的表格。 (g取10 m/s2)
所选择的参考平面 小球在A点 的重力势能 小球在B点的重力势能 整个下落过程中小球重力做的功 整个下落过程中小球重力势能的变化量
桌面
地面
6 J
10 J
-4 J
0
10 J
10 J
减少10 J
减少10 J
重力势能具有相对性,重力势能的变化量具有绝对性。
(1)在表格的空白处按要求填入数据。
(2)如果下落时有空气阻力,表中的数据是否会改变?
解:
如果下落时有空气阻力,表中的数据不会改变。
