【解析版】吉林省吉林市普通高中2014届高三上学期摸底测试数学(文)试题
文档属性
| 名称 | 【解析版】吉林省吉林市普通高中2014届高三上学期摸底测试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 250.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-08 15:57:10 | ||
图片预览




文档简介
吉林市普通中学2013—2014学年度高中毕业班摸底测试
数 学(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共22小题,共150分,共4页,考试时间120分钟,考试结束后,将答题卡和试题卷一并交回。
注意事项:
1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12题,每小题5分,共60分,在每小题给出的四个选项中,只有一个是符合题目要求。
1.设集合U={0,l,2,3,4,5,6},M ={l,3,5},N={4,5,6},则=
A. {0,2,4,6} B. {4, 5,6}
C. {4, 6} D. {0, 1, 2, 3, 4, 5, 6}
【答案】C
【解析】因为M ={l,3,5},所以,又因为N={4,5,6},,所以= {4, 6}。
2. 设i为虚数单位,则复数=
A. B. C. D.
【答案】A
【解析】。
3. 抛物线的焦点坐标是
A.(2,0) B.(0,2) C.(l,0) D.(0,1)
【答案】D
【解析】易知抛物线的焦点在y轴上,所以其焦点坐标为(0,1)。
4. ,若,则
A. 0 B. 3 C. D.
【答案】A
【解析】因为,所以,所以,所以。
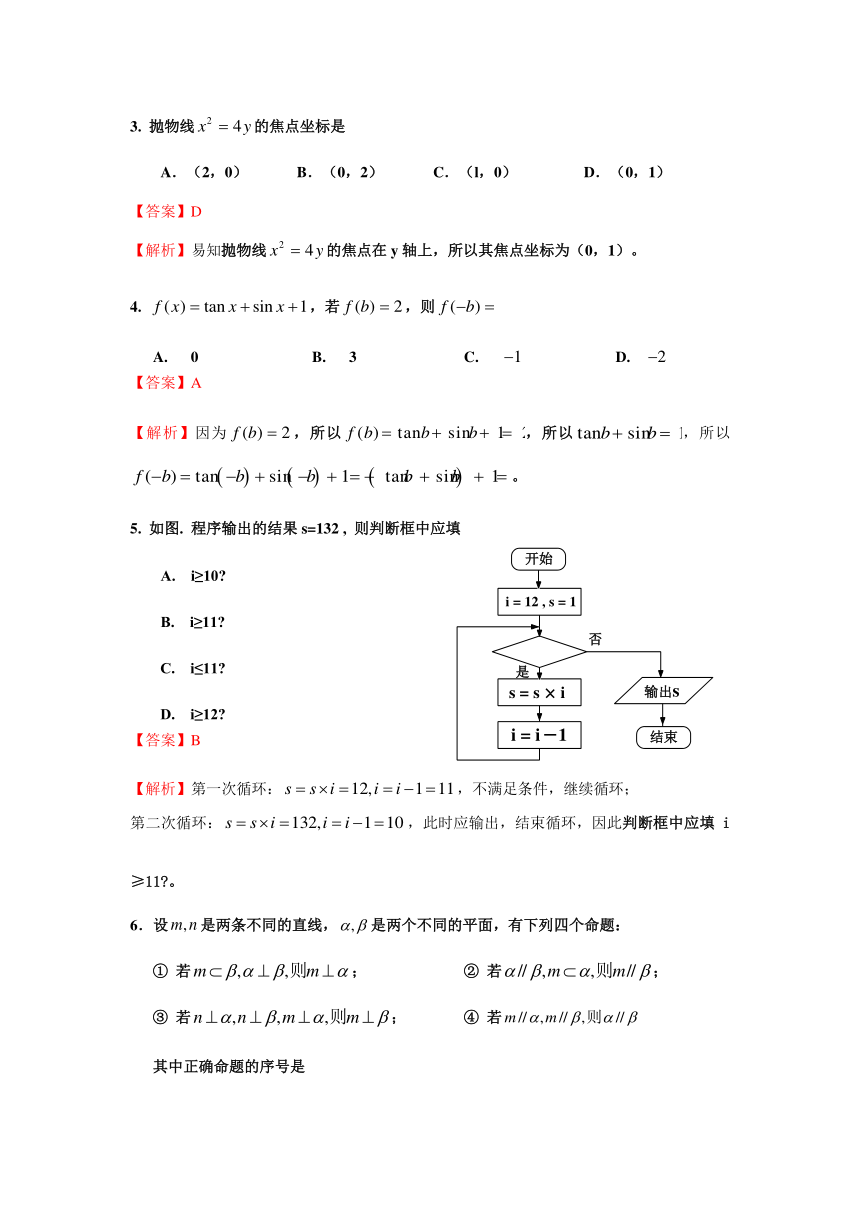
5. 如图. 程序输出的结果s=132 , 则判断框中应填
A. i≥10?
B. i≥11?
C. i≤11?
D. i≥12?
【答案】B
【解析】第一次循环:,不满足条件,继续循环;
第二次循环:,此时应输出,结束循环,因此判断框中应填i≥11?。
6.设是两条不同的直线,是两个不同的平面,有下列四个命题:
① 若; ② 若;
③ 若; ④ 若 其中正确命题的序号是
A. ①③ B. ①② C. ③④ D. ②③
【答案】D
【解析】① 若错误,的关系可能是平行、相交或者在平面内;
② 若正确,此为面面平行的性质定理;
③ 若正确,因为
④ 若,可能平行、相交。
7. 直线和圆的位置关系是
A.相离 B.相切
C.相交不过圆心 D.相交过圆心
【答案】A
【解析】易知的圆心为(0,2),半径为2,圆心到直线的距离为,所以直线和圆的位置关系是相离。
8. 已知向量,向量,且,则的值是
A. B. C. D.
【答案】C
【解析】因为,所以。
9.右图是某四棱锥的三视图,则该几何体的表面积等于
A.
B.
C.
D.
【答案】B
【解析】由三视图知,这是一个底面是矩形的四棱锥,矩形的长和宽分别是6,2,底面上的高与底面交于底面一条边的中点,四棱锥的高是4,所以四棱锥的表面积是。
10. 已知数列,,若该数列是递减数列,则实数的取值范围是
A. B.
C. D.
【答案】A
【解析】因为对于任意的n∈N*,恒成立,所以an+1-an=-2(n+1)2+λ(n+1)+2n2-λn=-4n-2+λ,因为{an}是递减数列,所以an+1-an<0,所以-4n-2+λ<0,即λ<4n+2,因为n=1时,4n+2取得最小值为6,所以λ<6.
11. 已知双曲线的右焦点F,直线与其渐近线交于A,B
两点,且为钝角三角形,则双曲线离心率的取值范围是 A. () B. (1,)
C. () D. (1,)
【答案】D
【解析】设直线与x轴的交点为C,A为第一象限的点,则:,若满足△为钝角三角形,需满足∠AFC>450,即,化简,得e∈(1,).
12. 设函数的最小值为,则实数的取值范围是
A. B.
C. D.
【答案】A
【解析】因为函数的最小值为,所以,所以实数的取值范围是。
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.
13.在△中,角所对的边分别为,已知,,.
则=
【答案】
【解析】由余弦定理得:。
14. 设变量满足约束条件,则的最大值是
【答案】5
【解析】画出约束条件的可行域,由可行域知:目标函数过点(2,3)时取最大值,最大值为5.
15. 边长是的正内接于体积是的球,则球面上的点到平面的最大距离为
【答案】
【解析】因为球的体积为,即,所以,设正的中心为D,连接OD,AD,OA,则OD⊥面ABC,且OA= ,AD= ,所以OD= ,所以球面上的点到平面的最大距离为。
16. 下列说法:
① “,使>3”的否定是“,使3”;
② 函数的最小正周期是;
③ “在中,若,则”的逆命题是真命题;
④ “”是“直线和直线垂直”的充要条件;其中正确的说法是 (只填序号).
【答案】①②
【解析】① “,使>3”的否定是“,使3”,正确;
② 因为,所以 函数的最小正周期是;
③ “在中,若,则”的逆命题是“在中,若,则”,在△ABC中,若A>B?a>b?2rsinA>2rsinB?sinA>sinB,故③正确;
④ 由 ,所以“”是“直线和直线垂直”的充要错误。
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
在锐角中,
(Ⅰ)求角的大小
(Ⅱ)求的取值范围
18.(本小题满分12分)
公差不为零的等差数列{}中,,又成等比数列. (Ⅰ)求数列{}的通项公式. (Ⅱ)设,求数列{}的前n项和.
19.(本小题满分12分)
某校高三期末统一测试,随机抽取一部分学生的数学成绩分组统计如下表:
(Ⅰ)求出表中、、、的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
分组
频数
频率
合计
(Ⅱ)若全校参加本次考试的学生有600人,试估计这次测试中全校成绩在分以上的人数;
(Ⅲ)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分的概率.
20.(本小题满分12分)
在四棱锥中,底面是正方形,侧面是正三角形,平面
底面.
(Ⅰ)如果为线段VC的中点,求证:平面;
(Ⅱ)如果正方形的边长为2, 求三棱锥的体积
21.(本小题满分12分)
已知椭圆()右顶点到右焦点的距离为,短轴长为.
(Ⅰ)求椭圆的方程;
(Ⅱ)过左焦点的直线与椭圆分别交于、两点,若线段的长为,
求直线的方程.
22. (本小题满分12分)
已知是的一个极值点
(Ⅰ) 求的值;
(Ⅱ) 求函数的单调递减区间;
(Ⅲ)设,试问过点可作多少条直线与曲线相切?请说明理由.
命题、校对:孙长青
吉林市普通中学2013—2014学年度高中毕业班摸底测试
数 学(文科)参考答案与评分标准
一、
1
2
3
4
5
6
7
8
9
10
11
12
C
A
D
A
B
D
A
C
B
A
D
A
二、13. 14. 5 15. 16. ①②
三、
17.解(1)由题意:即 -------------3分
∵ ∴ ∴即 --------------5分
(2)由(1)知:
∴ (7分)
∵为锐角三角形。
∴
∴ 又 ∴
∴ ……………………………(8分)
∴ ……………………………(10分)
18.解(1)设公差为d(d)
由已知得:, ,又因为,所以
, 所以 --------------------------------------6分
(2)由(1)得,因为
所以是以为首项,以8为公比的等比数列,所以 ----12分
19.(本小题满分12分)
解:(I)由频率分布表得, --------------------------------------1分
所以,--------------------------------------------------------------2分 ,----------3分 .………4分
…………6分
(Ⅱ)由题意知,全区90分以上学生估计为人. ………9分 (III)设考试成绩在内的3人分别为A、B、C;考试成绩在内的3人分别为a、b、c, 从不超过60分的6人中,任意抽取2人的结果有: (A,B),(A,C),(A ,a),(A,b),(A,c), (B,C),(B,a),(B,b),(B,c),(C,a), (C,b),(C,c),(a,b),(a,c),(b,c)共有15个.
设抽取的2人的分数均不大于30分为事件D. 则事件D含有3个结果: (A,B),(A,C) ,(B,C) ∴ . …………12分
20.(本小题满分12分)
解(Ⅰ)连结AC与BD交于点O, 连结OP
因为ABCD是正方形,所以OA=OC,又因为PV=PC
所以OP∥VA,又因为面PBD,所以平面--------6分
(Ⅱ)的面VAD内,过点V作VH⊥AD,因为平面
底面.所以VH⊥面
所以 ------------------- 12分
21.(本小题满分12分)
解:解:(Ⅰ)由题意,
解得.
即:椭圆方程为 ------------4分
(Ⅱ)当直线与轴垂直时,,
此时不符合题意故舍掉; -----------6分
当直线与轴不垂直时,设直线的方程为:,
代入消去得: .
设 ,则 -----------8分
所以 , ------------11分
由, ------------13分
所以直线或. ---------14分
22. (本小题满分12分)
解(I)因为是的一个极值点,所,经检验,适合题意,所以 ---------------------------------------------------------------3分
(II)定义域为,
所以函数的单调递减区间为 -------------------------------------------6分
(III),设过点(2,5)与曲线相切的切点为
所以, ------------9分
令,所在上单调递减,在上单调递增,因为,所以与x轴有两个交点,
所以过点可作2条直线与曲线相切 ------------------------------------------12分
数 学(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共22小题,共150分,共4页,考试时间120分钟,考试结束后,将答题卡和试题卷一并交回。
注意事项:
1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12题,每小题5分,共60分,在每小题给出的四个选项中,只有一个是符合题目要求。
1.设集合U={0,l,2,3,4,5,6},M ={l,3,5},N={4,5,6},则=
A. {0,2,4,6} B. {4, 5,6}
C. {4, 6} D. {0, 1, 2, 3, 4, 5, 6}
【答案】C
【解析】因为M ={l,3,5},所以,又因为N={4,5,6},,所以= {4, 6}。
2. 设i为虚数单位,则复数=
A. B. C. D.
【答案】A
【解析】。
3. 抛物线的焦点坐标是
A.(2,0) B.(0,2) C.(l,0) D.(0,1)
【答案】D
【解析】易知抛物线的焦点在y轴上,所以其焦点坐标为(0,1)。
4. ,若,则
A. 0 B. 3 C. D.
【答案】A
【解析】因为,所以,所以,所以。
5. 如图. 程序输出的结果s=132 , 则判断框中应填
A. i≥10?
B. i≥11?
C. i≤11?
D. i≥12?
【答案】B
【解析】第一次循环:,不满足条件,继续循环;
第二次循环:,此时应输出,结束循环,因此判断框中应填i≥11?。
6.设是两条不同的直线,是两个不同的平面,有下列四个命题:
① 若; ② 若;
③ 若; ④ 若 其中正确命题的序号是
A. ①③ B. ①② C. ③④ D. ②③
【答案】D
【解析】① 若错误,的关系可能是平行、相交或者在平面内;
② 若正确,此为面面平行的性质定理;
③ 若正确,因为
④ 若,可能平行、相交。
7. 直线和圆的位置关系是
A.相离 B.相切
C.相交不过圆心 D.相交过圆心
【答案】A
【解析】易知的圆心为(0,2),半径为2,圆心到直线的距离为,所以直线和圆的位置关系是相离。
8. 已知向量,向量,且,则的值是
A. B. C. D.
【答案】C
【解析】因为,所以。
9.右图是某四棱锥的三视图,则该几何体的表面积等于
A.
B.
C.
D.
【答案】B
【解析】由三视图知,这是一个底面是矩形的四棱锥,矩形的长和宽分别是6,2,底面上的高与底面交于底面一条边的中点,四棱锥的高是4,所以四棱锥的表面积是。
10. 已知数列,,若该数列是递减数列,则实数的取值范围是
A. B.
C. D.
【答案】A
【解析】因为对于任意的n∈N*,恒成立,所以an+1-an=-2(n+1)2+λ(n+1)+2n2-λn=-4n-2+λ,因为{an}是递减数列,所以an+1-an<0,所以-4n-2+λ<0,即λ<4n+2,因为n=1时,4n+2取得最小值为6,所以λ<6.
11. 已知双曲线的右焦点F,直线与其渐近线交于A,B
两点,且为钝角三角形,则双曲线离心率的取值范围是 A. () B. (1,)
C. () D. (1,)
【答案】D
【解析】设直线与x轴的交点为C,A为第一象限的点,则:,若满足△为钝角三角形,需满足∠AFC>450,即,化简,得e∈(1,).
12. 设函数的最小值为,则实数的取值范围是
A. B.
C. D.
【答案】A
【解析】因为函数的最小值为,所以,所以实数的取值范围是。
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.
13.在△中,角所对的边分别为,已知,,.
则=
【答案】
【解析】由余弦定理得:。
14. 设变量满足约束条件,则的最大值是
【答案】5
【解析】画出约束条件的可行域,由可行域知:目标函数过点(2,3)时取最大值,最大值为5.
15. 边长是的正内接于体积是的球,则球面上的点到平面的最大距离为
【答案】
【解析】因为球的体积为,即,所以,设正的中心为D,连接OD,AD,OA,则OD⊥面ABC,且OA= ,AD= ,所以OD= ,所以球面上的点到平面的最大距离为。
16. 下列说法:
① “,使>3”的否定是“,使3”;
② 函数的最小正周期是;
③ “在中,若,则”的逆命题是真命题;
④ “”是“直线和直线垂直”的充要条件;其中正确的说法是 (只填序号).
【答案】①②
【解析】① “,使>3”的否定是“,使3”,正确;
② 因为,所以 函数的最小正周期是;
③ “在中,若,则”的逆命题是“在中,若,则”,在△ABC中,若A>B?a>b?2rsinA>2rsinB?sinA>sinB,故③正确;
④ 由 ,所以“”是“直线和直线垂直”的充要错误。
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
在锐角中,
(Ⅰ)求角的大小
(Ⅱ)求的取值范围
18.(本小题满分12分)
公差不为零的等差数列{}中,,又成等比数列. (Ⅰ)求数列{}的通项公式. (Ⅱ)设,求数列{}的前n项和.
19.(本小题满分12分)
某校高三期末统一测试,随机抽取一部分学生的数学成绩分组统计如下表:
(Ⅰ)求出表中、、、的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
分组
频数
频率
合计
(Ⅱ)若全校参加本次考试的学生有600人,试估计这次测试中全校成绩在分以上的人数;
(Ⅲ)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分的概率.
20.(本小题满分12分)
在四棱锥中,底面是正方形,侧面是正三角形,平面
底面.
(Ⅰ)如果为线段VC的中点,求证:平面;
(Ⅱ)如果正方形的边长为2, 求三棱锥的体积
21.(本小题满分12分)
已知椭圆()右顶点到右焦点的距离为,短轴长为.
(Ⅰ)求椭圆的方程;
(Ⅱ)过左焦点的直线与椭圆分别交于、两点,若线段的长为,
求直线的方程.
22. (本小题满分12分)
已知是的一个极值点
(Ⅰ) 求的值;
(Ⅱ) 求函数的单调递减区间;
(Ⅲ)设,试问过点可作多少条直线与曲线相切?请说明理由.
命题、校对:孙长青
吉林市普通中学2013—2014学年度高中毕业班摸底测试
数 学(文科)参考答案与评分标准
一、
1
2
3
4
5
6
7
8
9
10
11
12
C
A
D
A
B
D
A
C
B
A
D
A
二、13. 14. 5 15. 16. ①②
三、
17.解(1)由题意:即 -------------3分
∵ ∴ ∴即 --------------5分
(2)由(1)知:
∴ (7分)
∵为锐角三角形。
∴
∴ 又 ∴
∴ ……………………………(8分)
∴ ……………………………(10分)
18.解(1)设公差为d(d)
由已知得:, ,又因为,所以
, 所以 --------------------------------------6分
(2)由(1)得,因为
所以是以为首项,以8为公比的等比数列,所以 ----12分
19.(本小题满分12分)
解:(I)由频率分布表得, --------------------------------------1分
所以,--------------------------------------------------------------2分 ,----------3分 .………4分
…………6分
(Ⅱ)由题意知,全区90分以上学生估计为人. ………9分 (III)设考试成绩在内的3人分别为A、B、C;考试成绩在内的3人分别为a、b、c, 从不超过60分的6人中,任意抽取2人的结果有: (A,B),(A,C),(A ,a),(A,b),(A,c), (B,C),(B,a),(B,b),(B,c),(C,a), (C,b),(C,c),(a,b),(a,c),(b,c)共有15个.
设抽取的2人的分数均不大于30分为事件D. 则事件D含有3个结果: (A,B),(A,C) ,(B,C) ∴ . …………12分
20.(本小题满分12分)
解(Ⅰ)连结AC与BD交于点O, 连结OP
因为ABCD是正方形,所以OA=OC,又因为PV=PC
所以OP∥VA,又因为面PBD,所以平面--------6分
(Ⅱ)的面VAD内,过点V作VH⊥AD,因为平面
底面.所以VH⊥面
所以 ------------------- 12分
21.(本小题满分12分)
解:解:(Ⅰ)由题意,
解得.
即:椭圆方程为 ------------4分
(Ⅱ)当直线与轴垂直时,,
此时不符合题意故舍掉; -----------6分
当直线与轴不垂直时,设直线的方程为:,
代入消去得: .
设 ,则 -----------8分
所以 , ------------11分
由, ------------13分
所以直线或. ---------14分
22. (本小题满分12分)
解(I)因为是的一个极值点,所,经检验,适合题意,所以 ---------------------------------------------------------------3分
(II)定义域为,
所以函数的单调递减区间为 -------------------------------------------6分
(III),设过点(2,5)与曲线相切的切点为
所以, ------------9分
令,所在上单调递减,在上单调递增,因为,所以与x轴有两个交点,
所以过点可作2条直线与曲线相切 ------------------------------------------12分
同课章节目录
