4.2.2等差数列的前n项和公式 课件(共16张PPT)
文档属性
| 名称 | 4.2.2等差数列的前n项和公式 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 818.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-02 11:07:50 | ||
图片预览






文档简介
(共16张PPT)
4.2.2 等差数列的
前n项和公式
1
(课前2分钟)
1.等差数列的定义?
2
旧知回顾:
2.等差数列的通项公式?
3.等差数列的等差中项?
2A=a+b
A=
4.等差数列的性质有哪些?
m+n=p+q
思(2分钟)自主预习
1.什么是等差数列的前n项和?
2.是如何推导出来的?
3
对于一个数列
记作即
如,对任意数列
4
泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶饰,图案之细致令人叫绝。
问题1:
传说泰姬陵 陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见示意图),奢靡之程度可见一斑。你知道这个图案一共花了多少颗圆宝石吗?
即: 1+2+3+······+100=?
→1
→2
→3
→4
→100
高斯出生于一个工匠家庭,幼时家境贫困,但聪敏异常.上小学四年级时,一次老师布置了一道数学习题:“把从1到100的自然数加起来,和是多少?”年仅10岁的小高斯略一思索就得到答案5050,这使老师非常吃惊.那么高斯是采用了什么方法来巧妙地计算出来的呢?
高斯(1777---1855), 德国数学家、物理学家和天文学家.他和牛顿、阿基米德,被誉为有史以来的三大数学家.有“数学王子”之称.
高斯“神速求和”的故事:
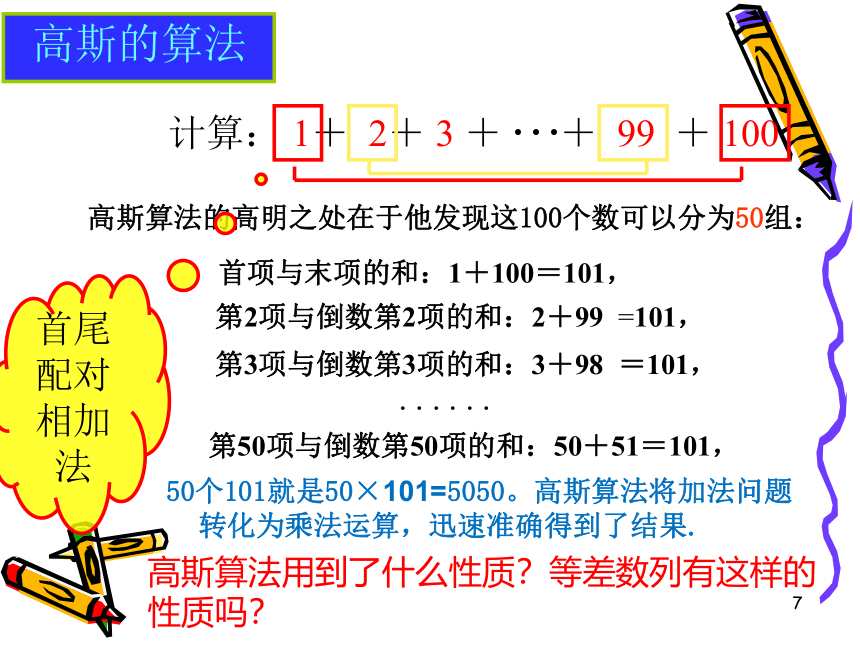
高斯的算法
计算: 1+ 2+ 3 + + 99 + 100
高斯算法的高明之处在于他发现这100个数可以分为50组:
首项与末项的和:1+100=101,
首尾配对相加法
7
第2项与倒数第2项的和:2+99 =101,
第3项与倒数第3项的和:3+98 =101,
· · · · · ·
第50项与倒数第50项的和:50+51=101,
50个101就是50×101=5050。高斯算法将加法问题转化为乘法运算,迅速准确得到了结果.
高斯算法用到了什么性质?等差数列有这样的性质吗?
合作探究
利用高斯算法如何求等差数列前n项和?
8
①n为偶数:
①n为奇数:
①
②
推导公式
倒序相加法
如何改进高斯的算法?
n可以是奇数也可以是偶数,如何避免讨论?
等差数列前n项和公式
一、两个公式的相同的是a1和n,不同的是:公式一中有an,公式二中有d 。 若a1,d, n, an中已知三个量就可以求出Sn 。
二、 a1,d, n, an,Sn五个量可“知三求二”。
(公式一)
(公式二)
例1、已知数列
(1)若=7,
(2)若=2,
(3)若=,
解:(1)因为=7,,根据公式
(2)因为=2,,所以,根据公式
(3)=,
整理得:
解得:
所以
例2、已知一个等差数列{an}的前10项的和是310,前20项的和是1220,由这些条件可以确定这个等差数列的首项和公差吗?
解:由题意知:
所以,由所给条件可以确定这个等差数列的首项和公差
练习、根据下列等差数列
(1)=20,
(2)d=,
(3)=,
(4)d=2,
课堂小结
(4)公式的应用:知三求一,
方程的思想方法
14
课后作业
一、书面作业:
1.已知等差数列{an},其中d=2,n=15, an =-10,求a1及sn。
2.在a,b之间插入10个数,使它们同这两个数成 等差数列,求这10个数的和。
3.课本23页练习2题~5题
二、课后思考:
等差数列的前n项和公式的推导方法除了倒序相加法还有没有其它方法呢
谢谢观看
下课!
16
4.2.2 等差数列的
前n项和公式
1
(课前2分钟)
1.等差数列的定义?
2
旧知回顾:
2.等差数列的通项公式?
3.等差数列的等差中项?
2A=a+b
A=
4.等差数列的性质有哪些?
m+n=p+q
思(2分钟)自主预习
1.什么是等差数列的前n项和?
2.是如何推导出来的?
3
对于一个数列
记作即
如,对任意数列
4
泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶饰,图案之细致令人叫绝。
问题1:
传说泰姬陵 陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见示意图),奢靡之程度可见一斑。你知道这个图案一共花了多少颗圆宝石吗?
即: 1+2+3+······+100=?
→1
→2
→3
→4
→100
高斯出生于一个工匠家庭,幼时家境贫困,但聪敏异常.上小学四年级时,一次老师布置了一道数学习题:“把从1到100的自然数加起来,和是多少?”年仅10岁的小高斯略一思索就得到答案5050,这使老师非常吃惊.那么高斯是采用了什么方法来巧妙地计算出来的呢?
高斯(1777---1855), 德国数学家、物理学家和天文学家.他和牛顿、阿基米德,被誉为有史以来的三大数学家.有“数学王子”之称.
高斯“神速求和”的故事:
高斯的算法
计算: 1+ 2+ 3 + + 99 + 100
高斯算法的高明之处在于他发现这100个数可以分为50组:
首项与末项的和:1+100=101,
首尾配对相加法
7
第2项与倒数第2项的和:2+99 =101,
第3项与倒数第3项的和:3+98 =101,
· · · · · ·
第50项与倒数第50项的和:50+51=101,
50个101就是50×101=5050。高斯算法将加法问题转化为乘法运算,迅速准确得到了结果.
高斯算法用到了什么性质?等差数列有这样的性质吗?
合作探究
利用高斯算法如何求等差数列前n项和?
8
①n为偶数:
①n为奇数:
①
②
推导公式
倒序相加法
如何改进高斯的算法?
n可以是奇数也可以是偶数,如何避免讨论?
等差数列前n项和公式
一、两个公式的相同的是a1和n,不同的是:公式一中有an,公式二中有d 。 若a1,d, n, an中已知三个量就可以求出Sn 。
二、 a1,d, n, an,Sn五个量可“知三求二”。
(公式一)
(公式二)
例1、已知数列
(1)若=7,
(2)若=2,
(3)若=,
解:(1)因为=7,,根据公式
(2)因为=2,,所以,根据公式
(3)=,
整理得:
解得:
所以
例2、已知一个等差数列{an}的前10项的和是310,前20项的和是1220,由这些条件可以确定这个等差数列的首项和公差吗?
解:由题意知:
所以,由所给条件可以确定这个等差数列的首项和公差
练习、根据下列等差数列
(1)=20,
(2)d=,
(3)=,
(4)d=2,
课堂小结
(4)公式的应用:知三求一,
方程的思想方法
14
课后作业
一、书面作业:
1.已知等差数列{an},其中d=2,n=15, an =-10,求a1及sn。
2.在a,b之间插入10个数,使它们同这两个数成 等差数列,求这10个数的和。
3.课本23页练习2题~5题
二、课后思考:
等差数列的前n项和公式的推导方法除了倒序相加法还有没有其它方法呢
谢谢观看
下课!
16
