河北省保定市高阳中学2014届高三下学期周练数学试题(二十五)
文档属性
| 名称 | 河北省保定市高阳中学2014届高三下学期周练数学试题(二十五) |  | |
| 格式 | zip | ||
| 文件大小 | 90.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-08 16:13:15 | ||
图片预览

文档简介
高三数学周练二十五
圆的圆心和半径是:
A B C D
已知AB∥PQ,BC∥QR,∠ABC=,则∠PQR等于( )
A B C D 以上都不对
若则下列不等式中正确的是( )
若A(-2,3),B(3,-2),C(,m)三点共线,则m的值为( )
A B C -2 D 2
经平面外一点和平面内一点与平面垂直的平面有
A 1个 B 0 个 C 无数个 D 1个或无数个
直线与圆交于E、F两点,则EOF(O为原点)的面积为( )
A B C D
a,b,c表示直线,M表示平面,给出下列四个命题:①若a∥M,b∥M,则a∥b;②若bM,a∥b,则a∥M;③若a⊥c,b⊥c,则a∥b;④若a⊥M,b⊥M,则a∥b.其中正确命题的个数有
A 0个 B 1个 C 2个 D 3个
设,则的大小顺序是( )
A B C D
在空间直角坐标系中,点M(1,-2,3)关于xoy平面及z轴对称的点的坐标分别为 ,
等体积的球和正方体,它们的表面积的大小关系是_____(填”大于、小于或等于”).
正方体的棱长为,那么△ , 三棱锥A-A1B1D1的体积为
设直线与圆相切,则实数的值为
过点(1,2)且在两坐标轴上的截距相等的直线的方程________ ___
已知垂直平行四边形所在平面,若,平行则四边形一定是 .
15.已知且,求证:
16.体积为V的圆柱中,底面半径和圆柱的高为多少时,其表面积S最小?
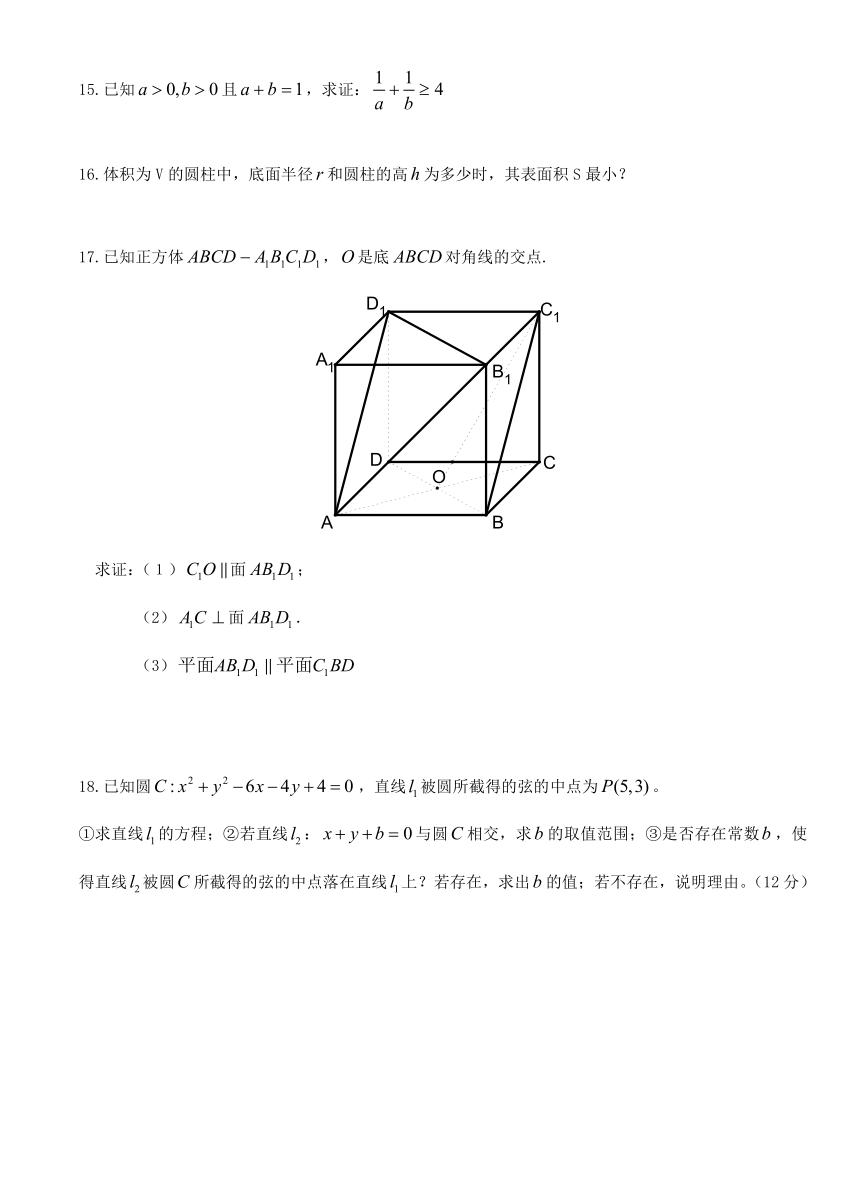
17.已知正方体,是底对角线的交点.
求证:(1)面;
(2)面.
(3)
18.已知圆,直线被圆所截得的弦的中点为。
①求直线的方程;②若直线:与圆相交,求的取值范围;③是否存在常数,使得直线被圆所截得的弦的中点落在直线上?若存在,求出的值;若不存在,说明理由。(12分)
答案
1-4 BBDA 5-8 DCBB
9.(1,-2,-3),(-1,2,3);10.小于 11.
12. ; 13. 14. 菱形
15.证明1:由于,根据柯西不等式得
又, ∴
另法:∵且
∴
16.解:由题得即
当且仅当即,时,圆柱体的表面积最小。
17.证明:(1)连结,设
连结, 是正方体
是平行四边形
且
又分别是的中点,且
是平行四边形
面,面
面
(2)面
又,
同理可证,
又
面
(3) 是正方体
∴AB1∥DC1 , AD1∥BC1
∴
18.解:①直线的方程为,②(即可用代数方法,以可用几何方法。)。③(设而不求),故存在满足条件的常数。
圆的圆心和半径是:
A B C D
已知AB∥PQ,BC∥QR,∠ABC=,则∠PQR等于( )
A B C D 以上都不对
若则下列不等式中正确的是( )
若A(-2,3),B(3,-2),C(,m)三点共线,则m的值为( )
A B C -2 D 2
经平面外一点和平面内一点与平面垂直的平面有
A 1个 B 0 个 C 无数个 D 1个或无数个
直线与圆交于E、F两点,则EOF(O为原点)的面积为( )
A B C D
a,b,c表示直线,M表示平面,给出下列四个命题:①若a∥M,b∥M,则a∥b;②若bM,a∥b,则a∥M;③若a⊥c,b⊥c,则a∥b;④若a⊥M,b⊥M,则a∥b.其中正确命题的个数有
A 0个 B 1个 C 2个 D 3个
设,则的大小顺序是( )
A B C D
在空间直角坐标系中,点M(1,-2,3)关于xoy平面及z轴对称的点的坐标分别为 ,
等体积的球和正方体,它们的表面积的大小关系是_____(填”大于、小于或等于”).
正方体的棱长为,那么△ , 三棱锥A-A1B1D1的体积为
设直线与圆相切,则实数的值为
过点(1,2)且在两坐标轴上的截距相等的直线的方程________ ___
已知垂直平行四边形所在平面,若,平行则四边形一定是 .
15.已知且,求证:
16.体积为V的圆柱中,底面半径和圆柱的高为多少时,其表面积S最小?
17.已知正方体,是底对角线的交点.
求证:(1)面;
(2)面.
(3)
18.已知圆,直线被圆所截得的弦的中点为。
①求直线的方程;②若直线:与圆相交,求的取值范围;③是否存在常数,使得直线被圆所截得的弦的中点落在直线上?若存在,求出的值;若不存在,说明理由。(12分)
答案
1-4 BBDA 5-8 DCBB
9.(1,-2,-3),(-1,2,3);10.小于 11.
12. ; 13. 14. 菱形
15.证明1:由于,根据柯西不等式得
又, ∴
另法:∵且
∴
16.解:由题得即
当且仅当即,时,圆柱体的表面积最小。
17.证明:(1)连结,设
连结, 是正方体
是平行四边形
且
又分别是的中点,且
是平行四边形
面,面
面
(2)面
又,
同理可证,
又
面
(3) 是正方体
∴AB1∥DC1 , AD1∥BC1
∴
18.解:①直线的方程为,②(即可用代数方法,以可用几何方法。)。③(设而不求),故存在满足条件的常数。
同课章节目录
