【新课标】4.2.2用列举法求概率(2) 课件(共29张PPT)
文档属性
| 名称 | 【新课标】4.2.2用列举法求概率(2) 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-03 08:56:24 | ||
图片预览








文档简介
(共29张PPT)
4.2.2用列举法求概率(2)
湘教版 九年级下
教学内容分析
上一节学习了用列表法求比较复杂事件的概率,
本节学习用树状图法求概率的方法、步骤,通过树状图来解决概率问题。
教学目标
1.掌握用“树状图法”求概率的方法、步骤;(重点)
2.能用树状图法求复杂事件的概率,解决概率的问题.(难点)
核心素养分析
本节利用树状图法求比较复杂事件的概率,总结了树状图法求概率的步骤,培养了学生随机性的认识,发展了学生应用概率知识的意识。
新知导入
1、写出一次试验中所有可能出现的结果数n.
2、写出事件A发生的所有结果数m.
3、计算事件的概率:P(A)=
列表法解决概率问题分“三步走”,分别是什么?
新知讲解
小明和小华做“剪刀、石头、布”的游戏,游戏规则是:若两人出的不同,则石头胜剪刀、剪刀胜布、布胜石头;若两人出的相同,则为平局.
动脑筋
新知讲解
(1)怎样表示和列举一次游戏的所有可能的结果?
(2)用A,B,C表示指定事件:
A:“小明胜”;B:“小华胜”; C: “平局”.
求事件A,B,C的概率.
新知讲解
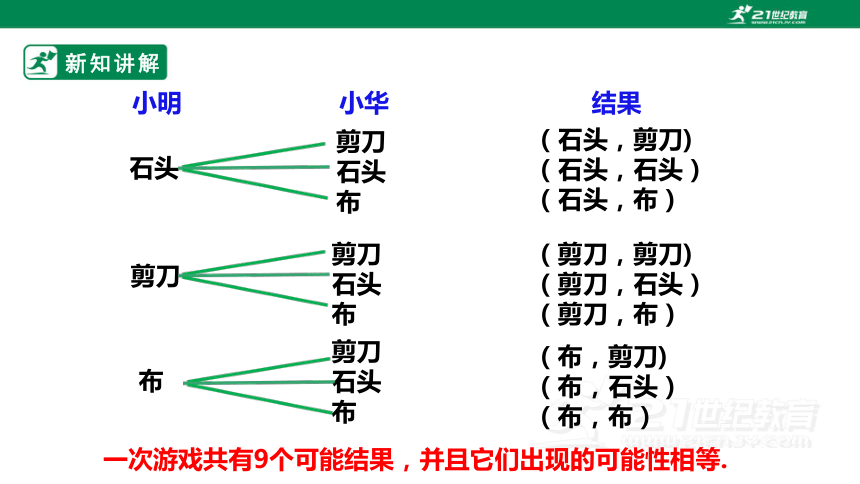
(1) 为了不重不漏地列出所有可能的结果, 除了列表法, 我们还可以借助树状图法.
分析
小明出石头,小华可能出剪刀、石头、布中的一种,
小明出剪刀,小华可能出剪刀、石头、布中的一种,
同理,小明出布,小华可能出剪刀、石头、布中的一种。
新知讲解
小明 小华 结果
布
剪刀
石头
剪刀
石头
布
剪刀
石头
布
剪刀
石头
布
(石头,剪刀)
(石头,石头)
(石头,布)
(剪刀,剪刀)
(剪刀,石头)
(剪刀,布)
(布,剪刀)
(布,石头)
(布,布)
一次游戏共有9个可能结果,并且它们出现的可能性相等.
新知讲解
(2)事件A发生的所有可能结果:
(石头,剪刀),(布,石头),(剪刀,布);
事件B发生的所有可能结果:
(石头,布),(剪刀,石头),(布,剪刀);
事件C发生的所有可能结果:
(石头,石头),(剪刀,剪刀),(布,布).
因此,
新知讲解
例2 如图,甲、乙、丙三人作传球的游戏.开始时,球在甲手中,每次传球,持球的人将球任意传给其余两人中的一人,如此传球3次.
新知讲解
(1)写出3次传球的所有结果(即传球的方式).
解: (1)一种可能传球的方式(结果)是,例如甲传给乙、乙传给丙、丙又传给甲,即依次落入乙、丙、甲手中,记为(乙,丙,甲).
新知讲解
第 1 次
第 2 次
第 3 次
结果
开始:
甲
乙
丙
甲
丙
甲
乙
乙
(乙、甲、乙)
丙
(乙、甲、丙)
甲
乙
乙
丙
甲
丙
(乙、丙、甲)
(乙、丙、乙)
(丙、甲、乙)
(丙、甲、丙)
(丙、乙、甲)
(丙、乙、丙)
共有8个可能结果,而且它们出现的可能性相等.
新知讲解
(2)指定事件A:“传球3次后,球又回到甲手中”写出A发生的所有可能结果;
传球3次后,球又回到甲手中,即事件A发生有2个可能结果:(乙,丙,甲),(丙,乙,甲).
(3)求P(A).
新知讲解
“树状图法”求概率的”三步走”
1、审清题意,写出每一步的结果。
2、在树状图的每一步后面写所有可能的结果。
3、写完所有结果,用符合条件的结果除以所有的结果,计算概率。
新知讲解
易错点:
当列举两次试验的可能结果,用列表法。
当列举两次或两次以上试验的可能结果,用树状图。
1.为了考察学生的综合素质,某市决定:九年级毕业生统一参加中考操作考试,根据今年的实际情况,中考实验操作考试科目为:P(物理)、C(化学)、B(生物),每科试题各为2道,考生随机抽取其中1道进行考试,小明和小丽是某校九年级学生,需参加实验考试.
(1)小明抽到化学实验的概率为______.
课堂练习
(2)若只从考试科目考虑,小明和小丽抽到不同科目的概率为多少?
课堂练习
(2)画树状图如下:
由树状图知,共有9种等可能结果,其中小明和小丽抽到不同科目的有6种结果,
∴小明和小丽抽到不同科目的概率为 .
课堂练习
2.从一副扑克牌中取出红桃J,Q,K和黑桃J,Q,K这两种花色的六张扑克牌.
(1)将这六张牌背面朝上,洗匀,随机抽取一张,求这张牌是红桃K的概率;
(2)将这三张红桃分为一组,三张黑桃分为一组,分别将这两组牌背面朝上洗匀,然后从这两组牌中各随机抽取一张,请利用列表或画树状图的方法,求其中一张是J一张Q的概率.
课堂练习
解:(1)将这六张牌背面朝上,洗匀,随机抽取一张,则这张牌是红桃K的概率为 。
(2)画树状图如图:
共有9个等可能的结果,其中一张是J一张Q的结果有2个,
∴其中一张是J一张Q的概率为.
课堂练习
3.某市“创建文明城市”活动如火如荼的展开,某中学为了搞好“创城”活动的宣传,校学生会就初三学生对当地“市情市况”的了解程度进行了一次调查测试,经过对测试成绩的分析,得到如图所示的两幅不完整的统计图 (A: 59分及以下;B:60-69分;70-79分; D:80-89分; E:90-100分) .请你根据图中提供的信息解答以下问题:
课堂练习
(1)在扇形统计图中,“90-100分”部分所对应的圆心角的度数为______度,并补全条形统计图;
(2)某班有三男两女得分在“90-100分”之间,现需从这五人中随机抽取两人到学校参加“共建文明城市,我在行动”的演讲比赛,请用树状图或者列表的方法求出刚好抽到一男一女参赛的概率.
课堂练习
解:(1)调查的总人数为300÷30%=1000(人),
A等级的人数为1000×10%=100(人),
D等级的人数为1000×35%=350(人),
E等级所对应的圆心角的度数为
补全条形统计图为:
课堂练习
解:(2)画树状图为:
共有20种等可能的结果数,其中刚好抽到一男一女参赛的结果数为12,所以刚好抽到一男一女参赛的概率= .
课堂总结
“树状图法”求概率的”三步走”
1、审清题意,写出每一步的结果。
2、在树状图的每一步后面所有可能的结果。
3、写完所有结果,用符合条件的结果除以所有的结果,计算概率。
板书设计
4.2.2 用列举法求概率(2)
1.树状图
2.用树状图法求概率
作业布置
必做题:课本习题4.2的第4~5题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.2.2用列举法求概率(2)
湘教版 九年级下
教学内容分析
上一节学习了用列表法求比较复杂事件的概率,
本节学习用树状图法求概率的方法、步骤,通过树状图来解决概率问题。
教学目标
1.掌握用“树状图法”求概率的方法、步骤;(重点)
2.能用树状图法求复杂事件的概率,解决概率的问题.(难点)
核心素养分析
本节利用树状图法求比较复杂事件的概率,总结了树状图法求概率的步骤,培养了学生随机性的认识,发展了学生应用概率知识的意识。
新知导入
1、写出一次试验中所有可能出现的结果数n.
2、写出事件A发生的所有结果数m.
3、计算事件的概率:P(A)=
列表法解决概率问题分“三步走”,分别是什么?
新知讲解
小明和小华做“剪刀、石头、布”的游戏,游戏规则是:若两人出的不同,则石头胜剪刀、剪刀胜布、布胜石头;若两人出的相同,则为平局.
动脑筋
新知讲解
(1)怎样表示和列举一次游戏的所有可能的结果?
(2)用A,B,C表示指定事件:
A:“小明胜”;B:“小华胜”; C: “平局”.
求事件A,B,C的概率.
新知讲解
(1) 为了不重不漏地列出所有可能的结果, 除了列表法, 我们还可以借助树状图法.
分析
小明出石头,小华可能出剪刀、石头、布中的一种,
小明出剪刀,小华可能出剪刀、石头、布中的一种,
同理,小明出布,小华可能出剪刀、石头、布中的一种。
新知讲解
小明 小华 结果
布
剪刀
石头
剪刀
石头
布
剪刀
石头
布
剪刀
石头
布
(石头,剪刀)
(石头,石头)
(石头,布)
(剪刀,剪刀)
(剪刀,石头)
(剪刀,布)
(布,剪刀)
(布,石头)
(布,布)
一次游戏共有9个可能结果,并且它们出现的可能性相等.
新知讲解
(2)事件A发生的所有可能结果:
(石头,剪刀),(布,石头),(剪刀,布);
事件B发生的所有可能结果:
(石头,布),(剪刀,石头),(布,剪刀);
事件C发生的所有可能结果:
(石头,石头),(剪刀,剪刀),(布,布).
因此,
新知讲解
例2 如图,甲、乙、丙三人作传球的游戏.开始时,球在甲手中,每次传球,持球的人将球任意传给其余两人中的一人,如此传球3次.
新知讲解
(1)写出3次传球的所有结果(即传球的方式).
解: (1)一种可能传球的方式(结果)是,例如甲传给乙、乙传给丙、丙又传给甲,即依次落入乙、丙、甲手中,记为(乙,丙,甲).
新知讲解
第 1 次
第 2 次
第 3 次
结果
开始:
甲
乙
丙
甲
丙
甲
乙
乙
(乙、甲、乙)
丙
(乙、甲、丙)
甲
乙
乙
丙
甲
丙
(乙、丙、甲)
(乙、丙、乙)
(丙、甲、乙)
(丙、甲、丙)
(丙、乙、甲)
(丙、乙、丙)
共有8个可能结果,而且它们出现的可能性相等.
新知讲解
(2)指定事件A:“传球3次后,球又回到甲手中”写出A发生的所有可能结果;
传球3次后,球又回到甲手中,即事件A发生有2个可能结果:(乙,丙,甲),(丙,乙,甲).
(3)求P(A).
新知讲解
“树状图法”求概率的”三步走”
1、审清题意,写出每一步的结果。
2、在树状图的每一步后面写所有可能的结果。
3、写完所有结果,用符合条件的结果除以所有的结果,计算概率。
新知讲解
易错点:
当列举两次试验的可能结果,用列表法。
当列举两次或两次以上试验的可能结果,用树状图。
1.为了考察学生的综合素质,某市决定:九年级毕业生统一参加中考操作考试,根据今年的实际情况,中考实验操作考试科目为:P(物理)、C(化学)、B(生物),每科试题各为2道,考生随机抽取其中1道进行考试,小明和小丽是某校九年级学生,需参加实验考试.
(1)小明抽到化学实验的概率为______.
课堂练习
(2)若只从考试科目考虑,小明和小丽抽到不同科目的概率为多少?
课堂练习
(2)画树状图如下:
由树状图知,共有9种等可能结果,其中小明和小丽抽到不同科目的有6种结果,
∴小明和小丽抽到不同科目的概率为 .
课堂练习
2.从一副扑克牌中取出红桃J,Q,K和黑桃J,Q,K这两种花色的六张扑克牌.
(1)将这六张牌背面朝上,洗匀,随机抽取一张,求这张牌是红桃K的概率;
(2)将这三张红桃分为一组,三张黑桃分为一组,分别将这两组牌背面朝上洗匀,然后从这两组牌中各随机抽取一张,请利用列表或画树状图的方法,求其中一张是J一张Q的概率.
课堂练习
解:(1)将这六张牌背面朝上,洗匀,随机抽取一张,则这张牌是红桃K的概率为 。
(2)画树状图如图:
共有9个等可能的结果,其中一张是J一张Q的结果有2个,
∴其中一张是J一张Q的概率为.
课堂练习
3.某市“创建文明城市”活动如火如荼的展开,某中学为了搞好“创城”活动的宣传,校学生会就初三学生对当地“市情市况”的了解程度进行了一次调查测试,经过对测试成绩的分析,得到如图所示的两幅不完整的统计图 (A: 59分及以下;B:60-69分;70-79分; D:80-89分; E:90-100分) .请你根据图中提供的信息解答以下问题:
课堂练习
(1)在扇形统计图中,“90-100分”部分所对应的圆心角的度数为______度,并补全条形统计图;
(2)某班有三男两女得分在“90-100分”之间,现需从这五人中随机抽取两人到学校参加“共建文明城市,我在行动”的演讲比赛,请用树状图或者列表的方法求出刚好抽到一男一女参赛的概率.
课堂练习
解:(1)调查的总人数为300÷30%=1000(人),
A等级的人数为1000×10%=100(人),
D等级的人数为1000×35%=350(人),
E等级所对应的圆心角的度数为
补全条形统计图为:
课堂练习
解:(2)画树状图为:
共有20种等可能的结果数,其中刚好抽到一男一女参赛的结果数为12,所以刚好抽到一男一女参赛的概率= .
课堂总结
“树状图法”求概率的”三步走”
1、审清题意,写出每一步的结果。
2、在树状图的每一步后面所有可能的结果。
3、写完所有结果,用符合条件的结果除以所有的结果,计算概率。
板书设计
4.2.2 用列举法求概率(2)
1.树状图
2.用树状图法求概率
作业布置
必做题:课本习题4.2的第4~5题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
