6.3 实践与探索 课件(共23张PPT) 2022-2023学年华东师大教版数学七年级下册
文档属性
| 名称 | 6.3 实践与探索 课件(共23张PPT) 2022-2023学年华东师大教版数学七年级下册 |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 07:49:10 | ||
图片预览






文档简介
(共23张PPT)
6.3 实践与探索
一元一次方程的实际应用
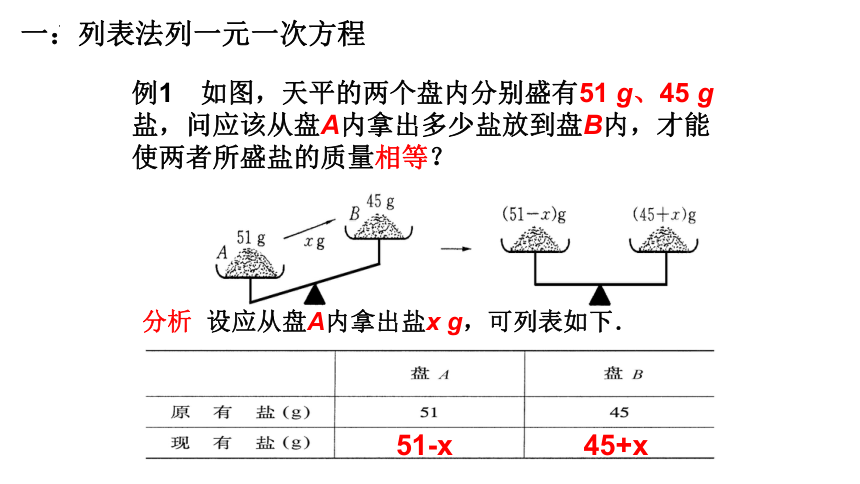
例1 如图,天平的两个盘内分别盛有51 g、45 g盐,问应该从盘A内拿出多少盐放到盘B内,才能使两者所盛盐的质量相等?
分析 设应从盘A内拿出盐x g,可列表如下.
51-x
45+x
一:列表法列一元一次方程
解: 设应从盘A内拿出盐x g放到盘B内,
则根据题意,得
51-x=45+x.
解这个方程,得
x=3.
经检验,符合题意.
答: 应从盘A内拿出3 g盐放到盘B内.
学校团委组织65名新团员为学校建花坛搬砖.女同学每人搬6块,男同学每人搬8块,每人搬了4次,共搬了1800块.问这些新团员中有多少名男同学?
分析 设新团员中有x名男同学,可列表如下.
例2
等量关系是什么?
8×4
65-x
32X
24(65-x)
x
男生搬砖数+女生搬砖数=总搬砖数
一:列表法列一元一次方程
解 :设新团员中有x名男同学,则女生(65-x)人,根据题意,得
32x+24(65-x)=1800.
解这个方程,得
x=30.
经检验,符合题意.
答: 新团员中有30名男同学.
新学年开始,某校三个年级为地震灾区捐款.经统计,七年级捐款数占全校三个年级捐款总数的,八年级捐款数是全校三个年级捐款数的平均数,已知九年级捐款 1964 元,求其他两个年级的捐款数.
评估任务1
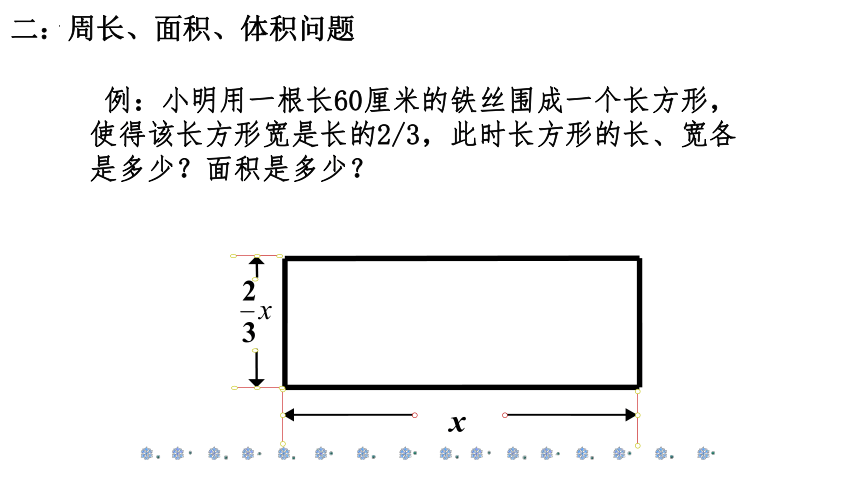
例:小明用一根长60厘米的铁丝围成一个长方形,使得该长方形宽是长的2/3,此时长方形的长、宽各是多少?面积是多少?
x
二:周长、面积、体积问题
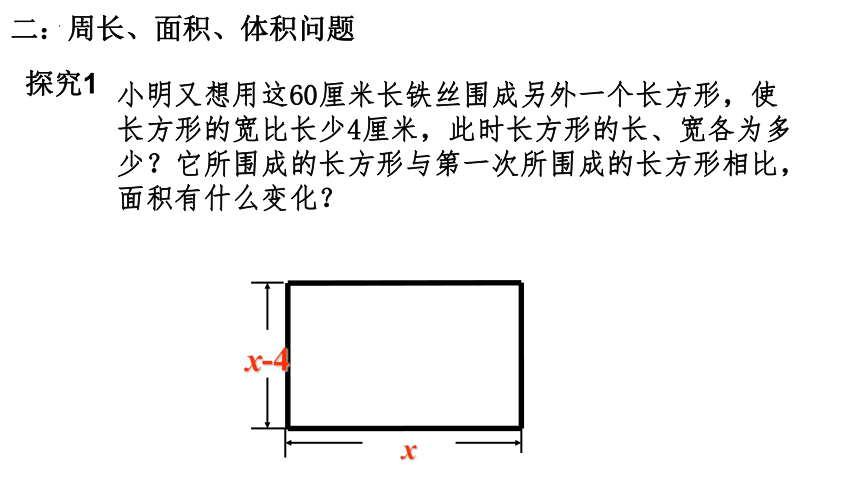
x-4
x
小明又想用这60厘米长铁丝围成另外一个长方形,使长方形的宽比长少4厘米,此时长方形的长、宽各为多少?它所围成的长方形与第一次所围成的长方形相比,面积有什么变化?
二:周长、面积、体积问题
探究1
若将上题中的“长方形的宽比长少4厘米”改为3厘米、2厘米、1厘米、0厘米(即长与宽相等),长方形的面积有什么变化?
同样长的铁丝围成怎样的四边形时面积最大?
探究2
二:周长、面积、体积问题
将一个底面直径是10厘米,高为36厘米的 “瘦长”形圆柱锻压成底面直径为20厘米的“矮胖”形圆柱,高变成了多少?
评估任务2
根据等量关系,列出方程:
解方程得: x=9
因此,高变成了 厘米。
9
等体积变形
问题关键
三:销售问题
1.某超市第一次用5500元购进了甲、乙两种商品,其中甲种商品150件,乙种商品100件.已知乙种商品每件进价比甲种商品每件进价贵5元.甲种商品售价为30元/件,乙种商品售价为 35 元/件.
探究 1:该超市第一次购进甲、乙两种商品每件各多少元
探究 2:该超市将第一次购进的甲、乙两种商品全部销售完后一共可获得多少利润
某文艺团体为“希望工程”募捐义演,成人票每张8元,学生票每张5元,如果本次义演共售出1 000张票,筹得票款6 950元,则成人票与学生票各售出多少张
(1)如果设售出的成人票为x张,请完成表格中的相关内容.
学生票 成人票
票数/张 x
票款/元
如果设售出的成人票为y张,则列出方程为:
评估任务3
小张和父亲预定搭乘公共汽车赶往火车站,去家乡看望爷爷.在行驶了一半路程时,小张向司机询问到达火车站的时间,司机估计继续乘公共汽车到火车站时火车将正好开出.根据司机的建议,小张和父亲随即下车改乘出租车,车速提高了一倍,结果赶在火车开车前15分钟到达火车站.已知公共汽车的平均速度是30千米/时,问小张家到火车站有多远
四:行程问题
分析1:
设:小张家到火车站的路程为 千米.
·
·
·
小张家
火车站
乘公共汽车
A
B
C
乘出租车
路程
路程
速度
30
速度
60
时间
时间
解法一
乘公共汽车时间
乘出租车时间
若都乘公共汽车到火车站所用时间
解:设小张家到火车站的路程为 千米.
可列得方程
答:小张家到火车站的路程为30千米.
分析2:
设乘公共汽车行驶 千米,则乘出租车行驶 千米.
·
·
·
小张家
火车站
乘公共汽车
A
B
C
乘出租车
路程
路程
速度
30
速度
60
时间
时间
解法二
乘公共汽车时间
乘出租车时间
解:设乘公共汽车行驶 千米,则乘出租车行驶 千米.
可列得方程
小张家到火车站的路程:
答:小张家到火车站的路程为30千米.
一条环形的跑道长 800 m,甲练习骑自行车,平均每分钟行500m,乙练习赛跑,平均每分钟跑200 m,两人同时同地反向而行,则他们经过多少分钟后首次相遇?
评估任务4
学校校办厂需制作一块广告牌,请来两名工人.已知师傅单独完成需4天,徒弟单独完成需6天.现由徒弟先做1天,再两个合作,完成后共得到报酬450元.如果按各人完成的工作量计算报酬,那么该如何分配
五:工程问题
徒弟先做1天
两个合作 天
徒弟先完成
师傅每天完成
徒弟每天完成
师傅完成
徒弟完成
总工作量记为1
解:设两个合作还需 天,
得方程
徒弟先做1天后,两个合作2天完成,
得到报酬450元.
徒弟、师傅工作每天均得报酬:
徒弟共得到报酬:
师傅共得到报酬:
答:徒弟共得到报酬270元,师傅共得到报酬180元.
解:设两人合作需 小时可以完成,
可列得方程
答:两人合作需6小时可以完成.
解这个方程
工作总量1
师傅每小时完成
师徒两人检修一条煤气管道,师傅单独完成要10小时,徒弟单独完成要15小时.现两人合作,需多少小时完成
两人合作每小时完成
徒弟每小时完成
评估任务5
6.3 实践与探索
一元一次方程的实际应用
例1 如图,天平的两个盘内分别盛有51 g、45 g盐,问应该从盘A内拿出多少盐放到盘B内,才能使两者所盛盐的质量相等?
分析 设应从盘A内拿出盐x g,可列表如下.
51-x
45+x
一:列表法列一元一次方程
解: 设应从盘A内拿出盐x g放到盘B内,
则根据题意,得
51-x=45+x.
解这个方程,得
x=3.
经检验,符合题意.
答: 应从盘A内拿出3 g盐放到盘B内.
学校团委组织65名新团员为学校建花坛搬砖.女同学每人搬6块,男同学每人搬8块,每人搬了4次,共搬了1800块.问这些新团员中有多少名男同学?
分析 设新团员中有x名男同学,可列表如下.
例2
等量关系是什么?
8×4
65-x
32X
24(65-x)
x
男生搬砖数+女生搬砖数=总搬砖数
一:列表法列一元一次方程
解 :设新团员中有x名男同学,则女生(65-x)人,根据题意,得
32x+24(65-x)=1800.
解这个方程,得
x=30.
经检验,符合题意.
答: 新团员中有30名男同学.
新学年开始,某校三个年级为地震灾区捐款.经统计,七年级捐款数占全校三个年级捐款总数的,八年级捐款数是全校三个年级捐款数的平均数,已知九年级捐款 1964 元,求其他两个年级的捐款数.
评估任务1
例:小明用一根长60厘米的铁丝围成一个长方形,使得该长方形宽是长的2/3,此时长方形的长、宽各是多少?面积是多少?
x
二:周长、面积、体积问题
x-4
x
小明又想用这60厘米长铁丝围成另外一个长方形,使长方形的宽比长少4厘米,此时长方形的长、宽各为多少?它所围成的长方形与第一次所围成的长方形相比,面积有什么变化?
二:周长、面积、体积问题
探究1
若将上题中的“长方形的宽比长少4厘米”改为3厘米、2厘米、1厘米、0厘米(即长与宽相等),长方形的面积有什么变化?
同样长的铁丝围成怎样的四边形时面积最大?
探究2
二:周长、面积、体积问题
将一个底面直径是10厘米,高为36厘米的 “瘦长”形圆柱锻压成底面直径为20厘米的“矮胖”形圆柱,高变成了多少?
评估任务2
根据等量关系,列出方程:
解方程得: x=9
因此,高变成了 厘米。
9
等体积变形
问题关键
三:销售问题
1.某超市第一次用5500元购进了甲、乙两种商品,其中甲种商品150件,乙种商品100件.已知乙种商品每件进价比甲种商品每件进价贵5元.甲种商品售价为30元/件,乙种商品售价为 35 元/件.
探究 1:该超市第一次购进甲、乙两种商品每件各多少元
探究 2:该超市将第一次购进的甲、乙两种商品全部销售完后一共可获得多少利润
某文艺团体为“希望工程”募捐义演,成人票每张8元,学生票每张5元,如果本次义演共售出1 000张票,筹得票款6 950元,则成人票与学生票各售出多少张
(1)如果设售出的成人票为x张,请完成表格中的相关内容.
学生票 成人票
票数/张 x
票款/元
如果设售出的成人票为y张,则列出方程为:
评估任务3
小张和父亲预定搭乘公共汽车赶往火车站,去家乡看望爷爷.在行驶了一半路程时,小张向司机询问到达火车站的时间,司机估计继续乘公共汽车到火车站时火车将正好开出.根据司机的建议,小张和父亲随即下车改乘出租车,车速提高了一倍,结果赶在火车开车前15分钟到达火车站.已知公共汽车的平均速度是30千米/时,问小张家到火车站有多远
四:行程问题
分析1:
设:小张家到火车站的路程为 千米.
·
·
·
小张家
火车站
乘公共汽车
A
B
C
乘出租车
路程
路程
速度
30
速度
60
时间
时间
解法一
乘公共汽车时间
乘出租车时间
若都乘公共汽车到火车站所用时间
解:设小张家到火车站的路程为 千米.
可列得方程
答:小张家到火车站的路程为30千米.
分析2:
设乘公共汽车行驶 千米,则乘出租车行驶 千米.
·
·
·
小张家
火车站
乘公共汽车
A
B
C
乘出租车
路程
路程
速度
30
速度
60
时间
时间
解法二
乘公共汽车时间
乘出租车时间
解:设乘公共汽车行驶 千米,则乘出租车行驶 千米.
可列得方程
小张家到火车站的路程:
答:小张家到火车站的路程为30千米.
一条环形的跑道长 800 m,甲练习骑自行车,平均每分钟行500m,乙练习赛跑,平均每分钟跑200 m,两人同时同地反向而行,则他们经过多少分钟后首次相遇?
评估任务4
学校校办厂需制作一块广告牌,请来两名工人.已知师傅单独完成需4天,徒弟单独完成需6天.现由徒弟先做1天,再两个合作,完成后共得到报酬450元.如果按各人完成的工作量计算报酬,那么该如何分配
五:工程问题
徒弟先做1天
两个合作 天
徒弟先完成
师傅每天完成
徒弟每天完成
师傅完成
徒弟完成
总工作量记为1
解:设两个合作还需 天,
得方程
徒弟先做1天后,两个合作2天完成,
得到报酬450元.
徒弟、师傅工作每天均得报酬:
徒弟共得到报酬:
师傅共得到报酬:
答:徒弟共得到报酬270元,师傅共得到报酬180元.
解:设两人合作需 小时可以完成,
可列得方程
答:两人合作需6小时可以完成.
解这个方程
工作总量1
师傅每小时完成
师徒两人检修一条煤气管道,师傅单独完成要10小时,徒弟单独完成要15小时.现两人合作,需多少小时完成
两人合作每小时完成
徒弟每小时完成
评估任务5
