9.5 三角形的中位线 课件(共19张PPT) 2022—2023学年苏科版数学八年级下册
文档属性
| 名称 | 9.5 三角形的中位线 课件(共19张PPT) 2022—2023学年苏科版数学八年级下册 |

|
|
| 格式 | zip | ||
| 文件大小 | 321.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 07:50:39 | ||
图片预览





文档简介
(共19张PPT)
9.5 三角形的中位线
情境创设
1
①如图,有一张三角形纸片,你能将其剪成两部分,使得其中一个是梯形,另一个是三角形吗?
A
B
C
②如图,有一张三角形纸片,你能将其剪成两部分,并将分成的两部分拼成一个平行四边形吗?
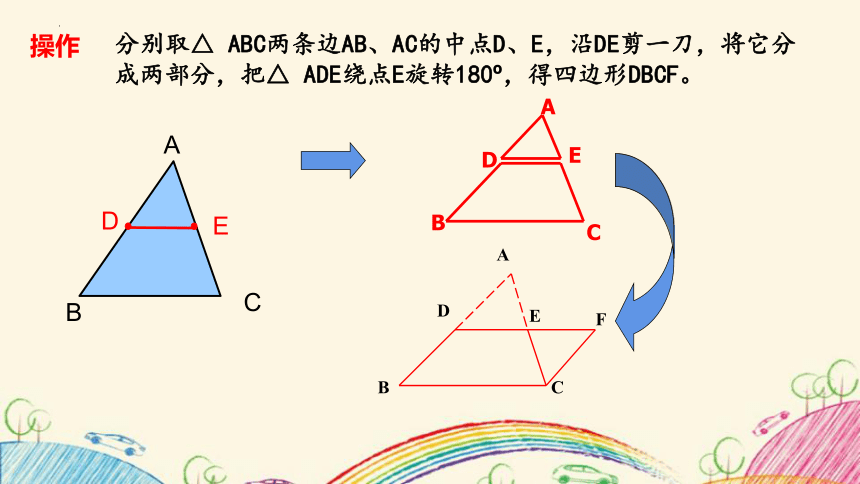
分别取△ ABC两条边AB、AC的中点D、E,沿DE剪一刀,将它分成两部分,把△ ADE绕点E旋转180 ,得四边形DBCF。
操作
A
B
C
D
E
A
D
E
B
C
D
E
A
B
C
F
新知生成
2
定义:连接三角形两边中点的线段叫三角形的中位线.
一个三角形有几条中位线?
三条
A
B
C
D
E
F
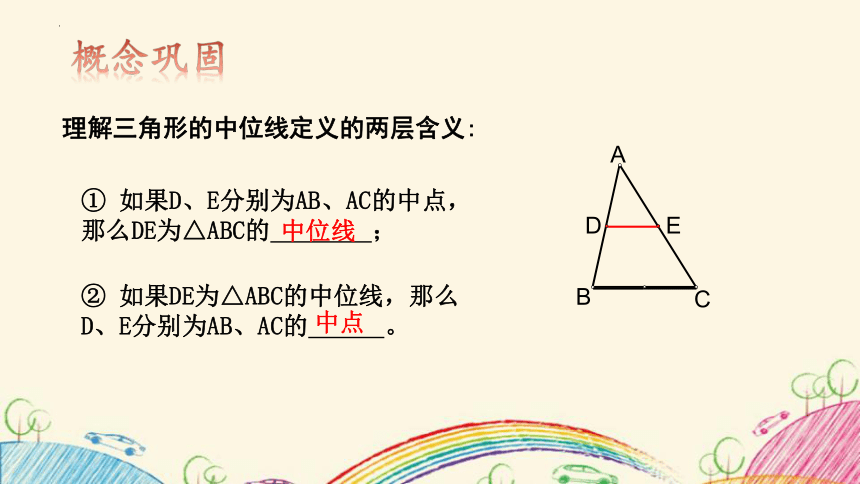
理解三角形的中位线定义的两层含义:
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。
① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;
C
B
A
E
D
中位线
中点
概念巩固
(1)相同点:都和边的中点有关;
(2)不同点:
三角形中位线的两个端点都是边的中点;
三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。
C
B
A
E
D
C
B
A
D
中线DC
中位线DE
三角形的中位线与中线有什么相同点和不同点?
概念对比
A
B
C
E
D
F
如图:三角形ABC中,点D、E、F分别是AB、BC、AC的中点.
(2)三角形的中线有______________
(1)三角形的中位线有____________
AE、BF、CD
DE、DF、EF
合作探究
3
合作探究
(1)D、E、F三个点在一条直线上吗?
D
E
A
B
C
F
(2)四边形BCFD是平行四边形吗?
(3)DE与BC有怎样的位置关系和数量关系?
三角形的中位线平行于第三边,且等于第三边的一半.
如图,已知△ ABC中,D、E分别是AB、AC的中点,求证:DE∥BC,DE = BC.
合作探究
C
E
D
F
B
A
证明:延长DE到F,使EF=DE,连接CF
∵D、E分别是AB、AC的中点
∴AE=CE、AD=BD
在△ ADE和△CFE中
AE=CE
∠AED=∠CEF
DE =FE
∴△ ADE ≌△CFE
∴∠F=∠ADE
∴CF∥AB,CF=AD
∵AD=BD
∴CF=BD
∴四边形DBCF是平行四边形
∴DE∥BC,DF=BC
∵DE= DF
∴DE= BC
1.如图:在△ABC中,DE是中位线。
(1)若∠ADE=60°,则∠B= ;
(2)若BC=8cm,则DE= cm.
(3)DE +BC=12cm,则BC= .
60°
4
8cm
6cm
2.若等腰△ABC的周长40cm,AB=AC=14cm,则中位线DE= .
E
A
B
C
D
及时训练
合作探究
思考:如图,怎样将一张三角形纸片剪成全等的四个三角形?
A
B
C
A
B
C
D
E
F
如图, D、E、F分别为AB、AC、BC的中点,①若△DEF的周长为10cm,则△ABC的周长= ;
②若AB=a,AC=b,BC=c , 则△DEF的周长=_______.
③若△ABC的面积等于20cm2,则△DEF的面积=_____;
④若△DEF的面积等于a, 则△ABC的面积=________.
及时训练
20cm
5cm2
a++
4a
补充: ①三角形三条中位线围成的三角形叫中点三角形;②中点三角形的周长等于原三角形周长的 ,面积等于原三角形面积的 .
例题讲解
4
例1:已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
例题讲解
变式:若保持上述条件不变,再加上AC=BD,则四边形EFGH是什么图形?
变式:若保持上述条件不变,再加上AC⊥BD,则四边形EFGH是什么图形?
变式:若保持上述条件不变,再加上AC=BD且AC⊥BD,则四边形EFGH是什么图形?
(2)顺次连接对角线互相垂直的任意四边形的各边中
点所得的四边形是_________;
(3)顺次连接对角线相等的任意四边形的各边中点
所得的四边形是_________.
(1)顺次连接任意四边形的各边中点所得的四边形是_________;
平行四边形
菱形
矩形
归纳:
1、定义:
连接三角形两边中点的线段叫做三角形的中位线.
2、三角形的中位线定理:
三角形的中位线平行于三角形的第三边,且等于第三边的一半.
数量关系:
位置关系:
DE∥BC
DE= BC.
C
A
B
D
E
小结思考
9.5 三角形的中位线
情境创设
1
①如图,有一张三角形纸片,你能将其剪成两部分,使得其中一个是梯形,另一个是三角形吗?
A
B
C
②如图,有一张三角形纸片,你能将其剪成两部分,并将分成的两部分拼成一个平行四边形吗?
分别取△ ABC两条边AB、AC的中点D、E,沿DE剪一刀,将它分成两部分,把△ ADE绕点E旋转180 ,得四边形DBCF。
操作
A
B
C
D
E
A
D
E
B
C
D
E
A
B
C
F
新知生成
2
定义:连接三角形两边中点的线段叫三角形的中位线.
一个三角形有几条中位线?
三条
A
B
C
D
E
F
理解三角形的中位线定义的两层含义:
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。
① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;
C
B
A
E
D
中位线
中点
概念巩固
(1)相同点:都和边的中点有关;
(2)不同点:
三角形中位线的两个端点都是边的中点;
三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。
C
B
A
E
D
C
B
A
D
中线DC
中位线DE
三角形的中位线与中线有什么相同点和不同点?
概念对比
A
B
C
E
D
F
如图:三角形ABC中,点D、E、F分别是AB、BC、AC的中点.
(2)三角形的中线有______________
(1)三角形的中位线有____________
AE、BF、CD
DE、DF、EF
合作探究
3
合作探究
(1)D、E、F三个点在一条直线上吗?
D
E
A
B
C
F
(2)四边形BCFD是平行四边形吗?
(3)DE与BC有怎样的位置关系和数量关系?
三角形的中位线平行于第三边,且等于第三边的一半.
如图,已知△ ABC中,D、E分别是AB、AC的中点,求证:DE∥BC,DE = BC.
合作探究
C
E
D
F
B
A
证明:延长DE到F,使EF=DE,连接CF
∵D、E分别是AB、AC的中点
∴AE=CE、AD=BD
在△ ADE和△CFE中
AE=CE
∠AED=∠CEF
DE =FE
∴△ ADE ≌△CFE
∴∠F=∠ADE
∴CF∥AB,CF=AD
∵AD=BD
∴CF=BD
∴四边形DBCF是平行四边形
∴DE∥BC,DF=BC
∵DE= DF
∴DE= BC
1.如图:在△ABC中,DE是中位线。
(1)若∠ADE=60°,则∠B= ;
(2)若BC=8cm,则DE= cm.
(3)DE +BC=12cm,则BC= .
60°
4
8cm
6cm
2.若等腰△ABC的周长40cm,AB=AC=14cm,则中位线DE= .
E
A
B
C
D
及时训练
合作探究
思考:如图,怎样将一张三角形纸片剪成全等的四个三角形?
A
B
C
A
B
C
D
E
F
如图, D、E、F分别为AB、AC、BC的中点,①若△DEF的周长为10cm,则△ABC的周长= ;
②若AB=a,AC=b,BC=c , 则△DEF的周长=_______.
③若△ABC的面积等于20cm2,则△DEF的面积=_____;
④若△DEF的面积等于a, 则△ABC的面积=________.
及时训练
20cm
5cm2
a++
4a
补充: ①三角形三条中位线围成的三角形叫中点三角形;②中点三角形的周长等于原三角形周长的 ,面积等于原三角形面积的 .
例题讲解
4
例1:已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
例题讲解
变式:若保持上述条件不变,再加上AC=BD,则四边形EFGH是什么图形?
变式:若保持上述条件不变,再加上AC⊥BD,则四边形EFGH是什么图形?
变式:若保持上述条件不变,再加上AC=BD且AC⊥BD,则四边形EFGH是什么图形?
(2)顺次连接对角线互相垂直的任意四边形的各边中
点所得的四边形是_________;
(3)顺次连接对角线相等的任意四边形的各边中点
所得的四边形是_________.
(1)顺次连接任意四边形的各边中点所得的四边形是_________;
平行四边形
菱形
矩形
归纳:
1、定义:
连接三角形两边中点的线段叫做三角形的中位线.
2、三角形的中位线定理:
三角形的中位线平行于三角形的第三边,且等于第三边的一半.
数量关系:
位置关系:
DE∥BC
DE= BC.
C
A
B
D
E
小结思考
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
