2022-2023学年京改版八年级数学下册14.7一次函数的应用达标练习(无答案)
文档属性
| 名称 | 2022-2023学年京改版八年级数学下册14.7一次函数的应用达标练习(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 491.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 08:43:39 | ||
图片预览

文档简介
14.7一次函数的应用达标练习
班级:________ 姓名:________
一、单选题(共 10 小题)
1、如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0)∠OAB的平分线交x轴于点C,点P、Q分别为线段AC、线段AO上的动点,则OP+PQ的最小值值为( )
A.2 B. C. D.
2、小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A.2.7分钟 B.2.8分钟 C.3分钟 D.3.2分钟
3、某游泳馆新推出了甲、乙两种消费卡,设游泳次数为时两种消费卡所需费用分别为,元,,与的函数图象如图所示,当游泳次数为30次时选择哪种消费卡更合算( )
A.甲种更合算 B.乙种更合算 C.两种一样合算 D.无法确定
4、“漏壶”是一种这个古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用表示漏水时间,表示壶底到水面的高度,下列图象适合表示与的对应关系的是( )
A. B. C. D.
5、如图1,正方形ABCD中,点E是边AD的中点,点P以1cm/s的速度从点A出发,沿运动到点C后,再沿线段CA到达点A.图2是点P运动时,△PEC的面积随时间变化的部分图象.根据图象判断:下列能表示点P在整个运动过程中y随x变化的完整图象为( )
A. B.
C. D.
6、如图,点C的坐标为(4,5),CA垂直于y轴于点A,D是线段AO上一点,且OD=4AD,点B从原点O出发,沿x轴正方向运动,CB与直线yx交于点E,取OE的中点F,则△CFD的面积为( )
A.10 B.9 C. D.8
7、已知两地相距240千米.早上9点甲车从A地出发去B地,20分钟后,乙车从B地出发去A地.两车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示,则下列描述不正确的是( )
A.甲车的速度是60千米/小时 B.乙车的速度是90千米/小时
C.甲车与乙车在早上10点相遇 D.乙车在到达A地
8、某市体育馆将举办明星足球赛,为此体育馆推出两种团体购票方案(设购票张数为张,购票总价为元).方案一:购票总价由图中的折线所表示的函数关系确定;方案二:提供元赞助后,每张票的票价为元.则两种方案购票总价相同时,的值为( )
A. B. C. D.
9、某施工队修一段长度为米的公路,施工队每天的效率相同,如表根据每天工程进度制作而成的.
施工时间天
累计完成施工量米
下列说法错误的是( )A.随着施工时间的逐渐增大,累计完成施工量也逐渐增大
B.施工时间每增加天,累计完成施工量就增加米
C.当施工时间为天时,累计完成施工量为米
D.若累计完成施工量为米,则施工时间为天
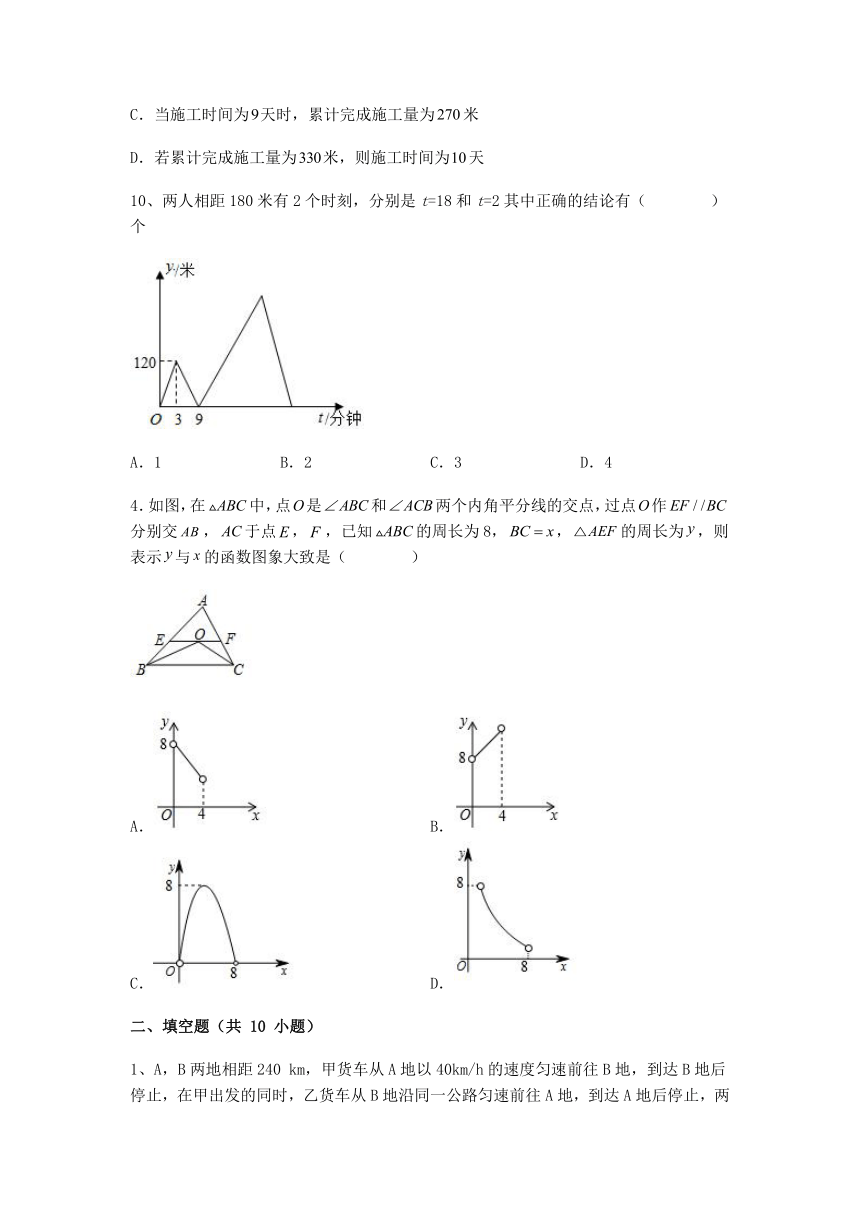
10、两人相距180米有2个时刻,分别是t=18和t=2其中正确的结论有( )个
A.1 B.2 C.3 D.4
4.如图,在中,点是和两个内角平分线的交点,过点作分别交,于点,,已知的周长为8,,的周长为,则表示与的函数图象大致是( )
A. B.
C. D.
二、填空题(共 10 小题)
1、A,B两地相距240 km,甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止,在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止,两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线所示.其中点C的坐标是,点D的坐标是,则点E的坐标是__________.
2、如图,在平面直角坐标系中,直线yx与x轴交于点A,且经过点B(2,a),在y轴上有一动点P,直线BC上有一动点M,已知C(3,0).
(1)a=_____;
(2)若△APM是以线段AM为斜边的等腰直角三角形,则点M的坐标是 _____.
3、如图,在平面直角坐标系中,点,点,点是直线上一点,且,则点的坐标为______.
4、星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示,则上午8:45小明离家的距离是__千米.
5、某长途汽车客运公司规定旅客可免费携带一定质量的行李.当行李的质量超过规定时,需付的行李费(元)与行李质量之间满足一次函数关系,部分对应值如下表:
… 30 40 50 …
(元) … 4 6 8 …
则旅客最多可免费携带行李的质量是______kg.
6、图中表示甲,乙两名选手在一次自行车越野赛中路程(千米)随时间(分)变化的图象,从图中可知比赛开始________分钟后两人第一次相遇.
7、在平面直角坐标系中,对于两点A、B,给出如下定义:以线段AB为直角边的等腰直角三角形称为点A、B的“对称三角形”.一次函数y=﹣x+4的图象与x轴、y轴分别交于点A和点B,在第一象限内,点A,B的“对称三角形”的另一个顶点坐标为_____.
8、甲、乙两名同学参加户外拓展活动,过程如下:甲、乙分别从直线赛道、两端同时出发,匀速相向而行.相遇时,甲将出发时在地抽取的任务单递给乙后继续向地前行,乙就原地执行任务,用时14分钟,再继续向地前行,此时甲尚未到达地.当甲和乙分别到达地和地后立即以原路原速返回并交换角色,即由乙在地抽取任务单,与甲相遇时交给甲,由甲原地执行任务,乙继续向地前行.抽取和递交任务单的时间忽略不计.甲、乙两名同学之间的距离(米与运动时间(分之间的关系如图所示.已知甲的速度为每分钟60米,且甲的速度小于乙的速度,现给出以下结论:
①两地距离1680米;
②出发10分钟,甲乙两人第一次相遇;
③乙的速度为每分钟100米;
④甲在出发后第44分钟时开始执行任务.
其中正确的是 __.(写出所有正确结论的序号)
9、如图,已知点C(1,0),直线y=﹣x+8与两坐标轴分别交于A、B两点,D、E分别是AB、OA上的动点,则△CDE周长的最小值是_____.
10、某体育用品商场为推销某一品牌运动服,先做了市场调查,得到数据如下表:
卖出价格x(元/件) 50 51 52 53
销售量P(件) 500 490 480 470
则P与x的函数关系式为________,当卖出价格为60元时,销售量为_______件.
三、解答题(共 6 小题)
1、如图1,一次函数y=x+3的图象与x轴相交于点A,与y轴相交于点B,点D是直线AB上的一个动点,CD⊥x轴于点C,点P是射线CD上的一个动点.
(1)求点A,B的坐标;
(2)如图2,当点D在第一象限,且AB=BD时,将ACP沿着AP翻折,当点C的对应点落在直线AB上时,求点P的坐标.
2、为抗击疫情,支援B市,A市某蔬菜公司紧急调运两车蔬菜运往B市.甲、乙两辆货车从A市出发前往B市,乙车行驶途中发生故障原地维修,此时甲车刚好到达B市.甲车卸载蔬菜后立即原路原速返回接应乙车,把乙车的蔬菜装上甲车后立即原路原速又运往B市.乙车维修完毕后立即返回A市.两车离A市的距离y(km)与乙车所用时间x(h)之间的函数图象如图所示.
(1)甲车速度是_______km/h,乙车出发时速度是_______km/h;
(2)求乙车返回过程中,乙车离A市的距离y(km)与乙车所用时间x(h)的函数解析式(不要求写出自变量的取值范围);
(3)乙车出发多少小时,两车之间的距离是120km?请直接写出答案.
3、近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息如表:
A型销售数量(台) B型销售数量(台) 总利润(元)
5 10 2500
10 5 2750
(1)每台A型空气净化器的销售利润是 元;每台B型空气净化器的销售利润是 元;
(2)该商场计划一次购进两种型号的空气净化器共80台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该商场销售完这80台空气净化器后的总利润最大,那么应该购进A型空气净化器 台;B型空气净化器 台.
(3)已知A型空气净化器的净化能力为300m3/小时,B型空气净化器的净化能力为200m3/小时.某长方体室内活动场地的总面积为300m2,室内墙高3m.该场地负责人计划购买7台空气净化器,每天花费30分钟将室内空气净化一新,如不考虑空气对流等因素,他至少要购买A型空气净化器多少台?
4、厦门市同安区A、B两村生产龙眼,A村生产的龙眼重量为200吨,B村生产的龙眼重量为300吨.现将这些龙眼运到C、D两个冷藏仓库,已知C仓库可存储240吨,D仓库可存储260吨;从A村运往C、D两处的费用分别为每吨20元和25元,从B村运往C、D两处的费用分别为每吨15元和18元设从A村运往C仓库的龙眼重量为x吨,A、B两村运往两仓库的龙眼运输费用的分别为元和元
(1)当x为何值时,A村和B村的运输费用相等;
(2)考虑到B村的经济承受能力,B村的龙眼运费不得超过4830元,在这种情况下,请问怎么样调运,才能使两村运费之和最小 求出这个最小值.
5、某班布置教室,同学们利用彩纸条粘成一环套一环的彩纸链,小橙同学测量了部分彩纸链的长度.
纸环数x(个) 1 2 3 4 5 6 ……
彩纸链长度y(cm) 19 34 49 64 79 94 ……
(1)把上表中x,y的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出相应的点.
(2)观察这些点发现,这些点是否在一条直线上,如果在一条直线上,求这条直线所对应的函数表达式.
(3)教室天花板为矩形,一条对角线长为10m,现需沿天花板对角线各拉一根彩纸链,则至少要用多少个纸环?
6、如图,在平面直角坐标系中,直线y=x+6交x轴于点A,交y轴于点B,交直线y=﹣2x+9于点C.
(1)点C的坐标是 .
(2)点M是直线AB上一点,点N是直线y=﹣2x+9上一点,连接线段MN,若MNx轴,且MN=6,求出所有符合条件的点M的坐标.
(3)在(2)的条件下,平面上是否存在点P,使得△BOP和△MNC全等,若存在,请直接写出点P的坐标,若不存在,请说明理由.
班级:________ 姓名:________
一、单选题(共 10 小题)
1、如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0)∠OAB的平分线交x轴于点C,点P、Q分别为线段AC、线段AO上的动点,则OP+PQ的最小值值为( )
A.2 B. C. D.
2、小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A.2.7分钟 B.2.8分钟 C.3分钟 D.3.2分钟
3、某游泳馆新推出了甲、乙两种消费卡,设游泳次数为时两种消费卡所需费用分别为,元,,与的函数图象如图所示,当游泳次数为30次时选择哪种消费卡更合算( )
A.甲种更合算 B.乙种更合算 C.两种一样合算 D.无法确定
4、“漏壶”是一种这个古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用表示漏水时间,表示壶底到水面的高度,下列图象适合表示与的对应关系的是( )
A. B. C. D.
5、如图1,正方形ABCD中,点E是边AD的中点,点P以1cm/s的速度从点A出发,沿运动到点C后,再沿线段CA到达点A.图2是点P运动时,△PEC的面积随时间变化的部分图象.根据图象判断:下列能表示点P在整个运动过程中y随x变化的完整图象为( )
A. B.
C. D.
6、如图,点C的坐标为(4,5),CA垂直于y轴于点A,D是线段AO上一点,且OD=4AD,点B从原点O出发,沿x轴正方向运动,CB与直线yx交于点E,取OE的中点F,则△CFD的面积为( )
A.10 B.9 C. D.8
7、已知两地相距240千米.早上9点甲车从A地出发去B地,20分钟后,乙车从B地出发去A地.两车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示,则下列描述不正确的是( )
A.甲车的速度是60千米/小时 B.乙车的速度是90千米/小时
C.甲车与乙车在早上10点相遇 D.乙车在到达A地
8、某市体育馆将举办明星足球赛,为此体育馆推出两种团体购票方案(设购票张数为张,购票总价为元).方案一:购票总价由图中的折线所表示的函数关系确定;方案二:提供元赞助后,每张票的票价为元.则两种方案购票总价相同时,的值为( )
A. B. C. D.
9、某施工队修一段长度为米的公路,施工队每天的效率相同,如表根据每天工程进度制作而成的.
施工时间天
累计完成施工量米
下列说法错误的是( )A.随着施工时间的逐渐增大,累计完成施工量也逐渐增大
B.施工时间每增加天,累计完成施工量就增加米
C.当施工时间为天时,累计完成施工量为米
D.若累计完成施工量为米,则施工时间为天
10、两人相距180米有2个时刻,分别是t=18和t=2其中正确的结论有( )个
A.1 B.2 C.3 D.4
4.如图,在中,点是和两个内角平分线的交点,过点作分别交,于点,,已知的周长为8,,的周长为,则表示与的函数图象大致是( )
A. B.
C. D.
二、填空题(共 10 小题)
1、A,B两地相距240 km,甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止,在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止,两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线所示.其中点C的坐标是,点D的坐标是,则点E的坐标是__________.
2、如图,在平面直角坐标系中,直线yx与x轴交于点A,且经过点B(2,a),在y轴上有一动点P,直线BC上有一动点M,已知C(3,0).
(1)a=_____;
(2)若△APM是以线段AM为斜边的等腰直角三角形,则点M的坐标是 _____.
3、如图,在平面直角坐标系中,点,点,点是直线上一点,且,则点的坐标为______.
4、星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示,则上午8:45小明离家的距离是__千米.
5、某长途汽车客运公司规定旅客可免费携带一定质量的行李.当行李的质量超过规定时,需付的行李费(元)与行李质量之间满足一次函数关系,部分对应值如下表:
… 30 40 50 …
(元) … 4 6 8 …
则旅客最多可免费携带行李的质量是______kg.
6、图中表示甲,乙两名选手在一次自行车越野赛中路程(千米)随时间(分)变化的图象,从图中可知比赛开始________分钟后两人第一次相遇.
7、在平面直角坐标系中,对于两点A、B,给出如下定义:以线段AB为直角边的等腰直角三角形称为点A、B的“对称三角形”.一次函数y=﹣x+4的图象与x轴、y轴分别交于点A和点B,在第一象限内,点A,B的“对称三角形”的另一个顶点坐标为_____.
8、甲、乙两名同学参加户外拓展活动,过程如下:甲、乙分别从直线赛道、两端同时出发,匀速相向而行.相遇时,甲将出发时在地抽取的任务单递给乙后继续向地前行,乙就原地执行任务,用时14分钟,再继续向地前行,此时甲尚未到达地.当甲和乙分别到达地和地后立即以原路原速返回并交换角色,即由乙在地抽取任务单,与甲相遇时交给甲,由甲原地执行任务,乙继续向地前行.抽取和递交任务单的时间忽略不计.甲、乙两名同学之间的距离(米与运动时间(分之间的关系如图所示.已知甲的速度为每分钟60米,且甲的速度小于乙的速度,现给出以下结论:
①两地距离1680米;
②出发10分钟,甲乙两人第一次相遇;
③乙的速度为每分钟100米;
④甲在出发后第44分钟时开始执行任务.
其中正确的是 __.(写出所有正确结论的序号)
9、如图,已知点C(1,0),直线y=﹣x+8与两坐标轴分别交于A、B两点,D、E分别是AB、OA上的动点,则△CDE周长的最小值是_____.
10、某体育用品商场为推销某一品牌运动服,先做了市场调查,得到数据如下表:
卖出价格x(元/件) 50 51 52 53
销售量P(件) 500 490 480 470
则P与x的函数关系式为________,当卖出价格为60元时,销售量为_______件.
三、解答题(共 6 小题)
1、如图1,一次函数y=x+3的图象与x轴相交于点A,与y轴相交于点B,点D是直线AB上的一个动点,CD⊥x轴于点C,点P是射线CD上的一个动点.
(1)求点A,B的坐标;
(2)如图2,当点D在第一象限,且AB=BD时,将ACP沿着AP翻折,当点C的对应点落在直线AB上时,求点P的坐标.
2、为抗击疫情,支援B市,A市某蔬菜公司紧急调运两车蔬菜运往B市.甲、乙两辆货车从A市出发前往B市,乙车行驶途中发生故障原地维修,此时甲车刚好到达B市.甲车卸载蔬菜后立即原路原速返回接应乙车,把乙车的蔬菜装上甲车后立即原路原速又运往B市.乙车维修完毕后立即返回A市.两车离A市的距离y(km)与乙车所用时间x(h)之间的函数图象如图所示.
(1)甲车速度是_______km/h,乙车出发时速度是_______km/h;
(2)求乙车返回过程中,乙车离A市的距离y(km)与乙车所用时间x(h)的函数解析式(不要求写出自变量的取值范围);
(3)乙车出发多少小时,两车之间的距离是120km?请直接写出答案.
3、近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息如表:
A型销售数量(台) B型销售数量(台) 总利润(元)
5 10 2500
10 5 2750
(1)每台A型空气净化器的销售利润是 元;每台B型空气净化器的销售利润是 元;
(2)该商场计划一次购进两种型号的空气净化器共80台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该商场销售完这80台空气净化器后的总利润最大,那么应该购进A型空气净化器 台;B型空气净化器 台.
(3)已知A型空气净化器的净化能力为300m3/小时,B型空气净化器的净化能力为200m3/小时.某长方体室内活动场地的总面积为300m2,室内墙高3m.该场地负责人计划购买7台空气净化器,每天花费30分钟将室内空气净化一新,如不考虑空气对流等因素,他至少要购买A型空气净化器多少台?
4、厦门市同安区A、B两村生产龙眼,A村生产的龙眼重量为200吨,B村生产的龙眼重量为300吨.现将这些龙眼运到C、D两个冷藏仓库,已知C仓库可存储240吨,D仓库可存储260吨;从A村运往C、D两处的费用分别为每吨20元和25元,从B村运往C、D两处的费用分别为每吨15元和18元设从A村运往C仓库的龙眼重量为x吨,A、B两村运往两仓库的龙眼运输费用的分别为元和元
(1)当x为何值时,A村和B村的运输费用相等;
(2)考虑到B村的经济承受能力,B村的龙眼运费不得超过4830元,在这种情况下,请问怎么样调运,才能使两村运费之和最小 求出这个最小值.
5、某班布置教室,同学们利用彩纸条粘成一环套一环的彩纸链,小橙同学测量了部分彩纸链的长度.
纸环数x(个) 1 2 3 4 5 6 ……
彩纸链长度y(cm) 19 34 49 64 79 94 ……
(1)把上表中x,y的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出相应的点.
(2)观察这些点发现,这些点是否在一条直线上,如果在一条直线上,求这条直线所对应的函数表达式.
(3)教室天花板为矩形,一条对角线长为10m,现需沿天花板对角线各拉一根彩纸链,则至少要用多少个纸环?
6、如图,在平面直角坐标系中,直线y=x+6交x轴于点A,交y轴于点B,交直线y=﹣2x+9于点C.
(1)点C的坐标是 .
(2)点M是直线AB上一点,点N是直线y=﹣2x+9上一点,连接线段MN,若MNx轴,且MN=6,求出所有符合条件的点M的坐标.
(3)在(2)的条件下,平面上是否存在点P,使得△BOP和△MNC全等,若存在,请直接写出点P的坐标,若不存在,请说明理由.
同课章节目录
