2022-2023学年八年级华东师大版数学下册17.2 函数的图象 课时练习(含答案)
文档属性
| 名称 | 2022-2023学年八年级华东师大版数学下册17.2 函数的图象 课时练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 08:48:13 | ||
图片预览



文档简介
17.2函数的图象
学校:___________姓名:___________班级:___________考号:___________
一、单选题(每小题4分,共48分)
1.小明的家在学校正南,正东方向处,如果以学校位置为原点,以正东、正北为正方向,则小明家用有序数对表示为( )
A. B. C. D.
2.在数轴上,用有序数对表示点的平移,若得到的数为1,得到的数为3,则得到的数为( ).
A.8 B. C.2 D.
3.在如图所示的平面直角坐标系中,点B的坐标为( )
A. B. C. D.
4.在平面直角坐标系中,点在第三象限,且Р到x轴和y轴的距离分别为8和5,则点P的坐标为( )
A. B. C. D.
5.不论m取何实数,点都不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.在平面直角坐标系中,若点在第二象限,则整数m的值为( )
A.1 B.2 C.3 D.4
7.如图,在某平面直角坐标系的网格中,点A的坐标为,点C的坐标为,则它的坐标原点为( )
A.点B B.点D C.点P D.点Q
8.如图是一块不规则的四边形地皮,各顶点坐标分别为,,,(图上一个单位长度表示10米),则这块地皮的面积是( ).
A.25 B.250 C.2500 D.2200
9.晚饭后彤彤和妈妈散步到小区旁边的公园,在公园中央的休息区聊了会儿天,然后一起跑步回家,下面能反映肜彤和妈妈离家的距离y与时间x的函数关系的大致图象是( )
A.B.C. D.
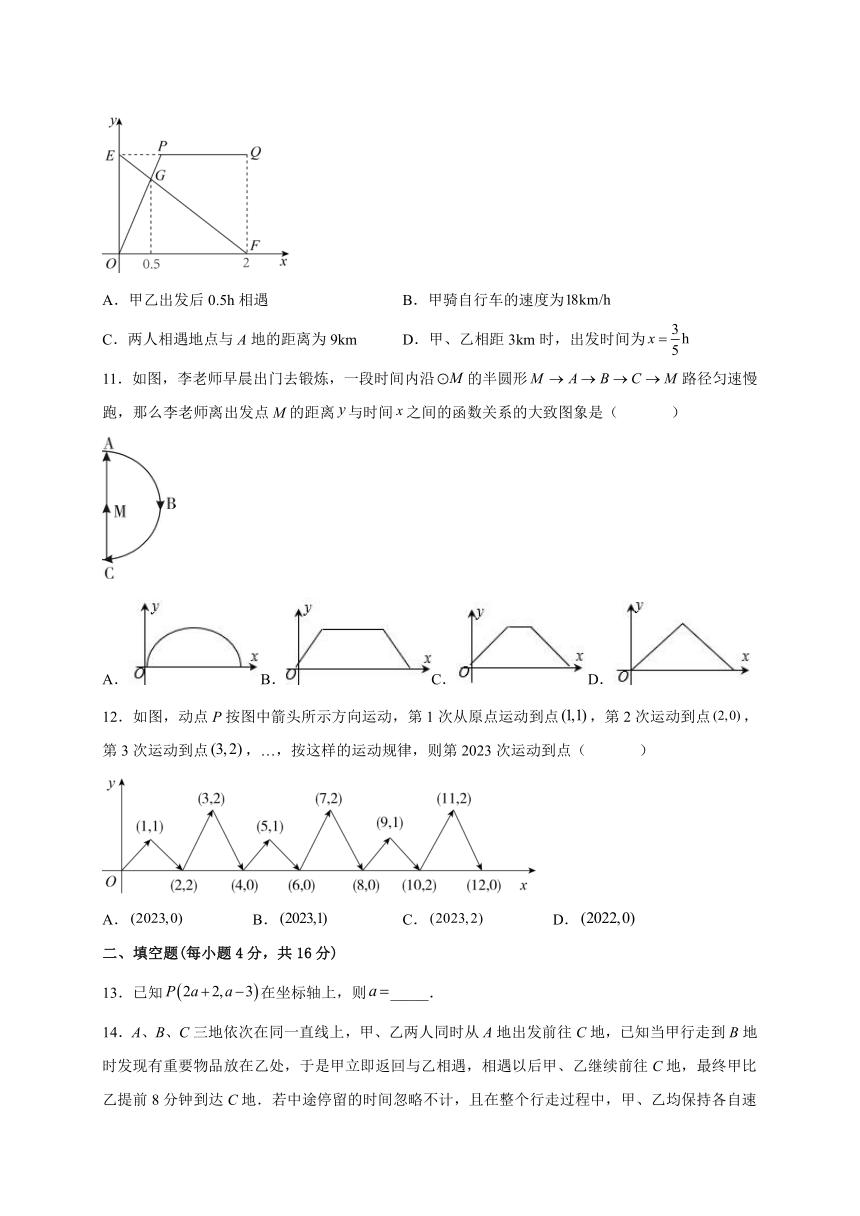
10.A、B两地相距12km,甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图所示的折线和线段EF分别表示甲、乙两人与A地的距离y(km)与时间x(h)之间的函数关系,且OP与EF交于点G.下列说法中错误的是( )
A.甲乙出发后0.5h相遇 B.甲骑自行车的速度为
C.两人相遇地点与A地的距离为9km D.甲、乙相距3km时,出发时间为
11.如图,李老师早晨出门去锻炼,一段时间内沿的半圆形路径匀速慢跑,那么李老师离出发点M的距离与时间之间的函数关系的大致图象是( )
A.B.C. D.
12.如图,动点P按图中箭头所示方向运动,第1次从原点运动到点,第2次运动到点,第3次运动到点,…,按这样的运动规律,则第2023次运动到点( )
A. B. C. D.
二、填空题(每小题4分,共16分)
13.已知在坐标轴上,则_____.
14.A、B、C三地依次在同一直线上,甲、乙两人同时从A地出发前往C地,已知当甲行走到B地时发现有重要物品放在乙处,于是甲立即返回与乙相遇,相遇以后甲、乙继续前往C地,最终甲比乙提前8分钟到达C地.若中途停留的时间忽略不计,且在整个行走过程中,甲、乙均保持各自速度匀速行走,甲、乙两人之间的距离y(米)与乙行走的时间x(分钟)之间的函数关系如图,则BC两地的距离为___________米.
15.已知点A,B的坐标分别为和,若轴,则___________.
16.如图,点,,,,…….根据这个规律,探究可得点的坐标是___________.
三、解答题(6个小题,共56分)
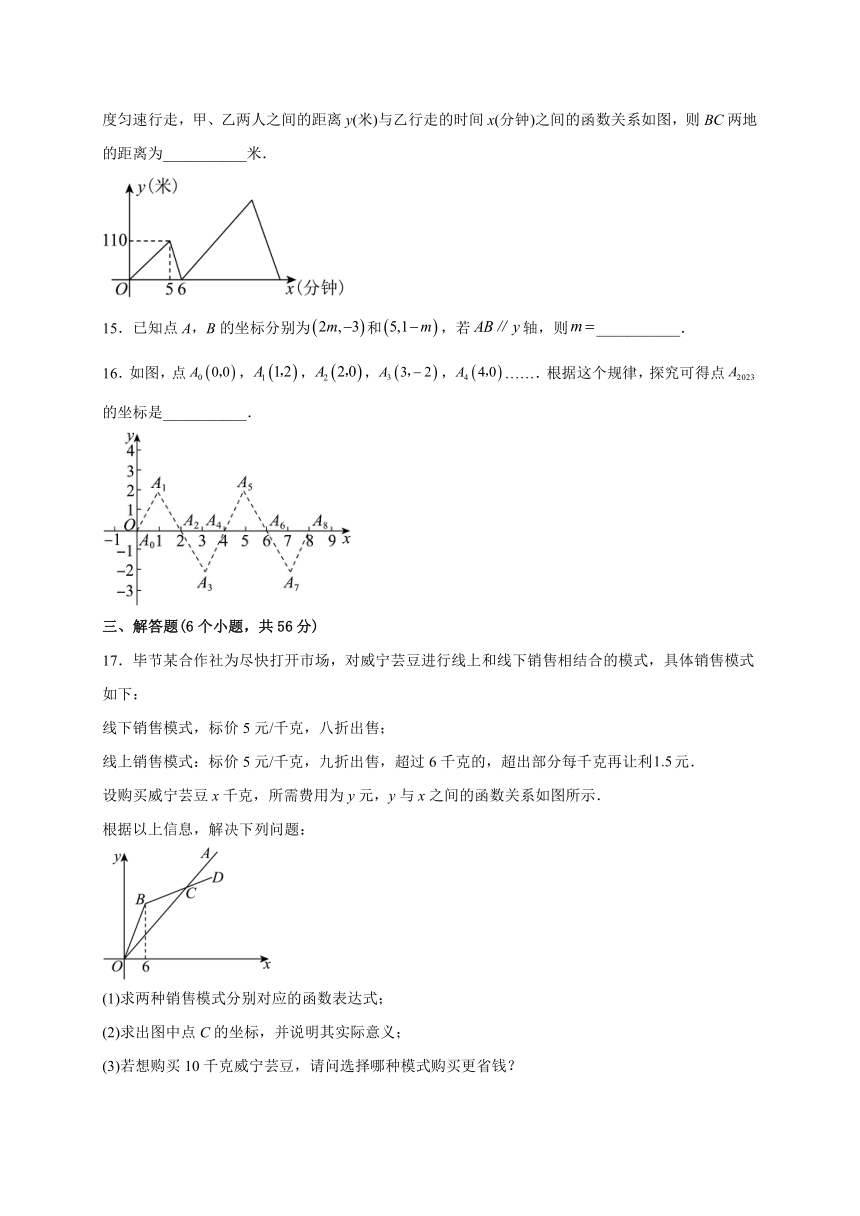
17.毕节某合作社为尽快打开市场,对威宁芸豆进行线上和线下销售相结合的模式,具体销售模式如下:
线下销售模式,标价5元/千克,八折出售;
线上销售模式:标价5元/千克,九折出售,超过6千克的,超出部分每千克再让利元.
设购买威宁芸豆x千克,所需费用为y元,y与x之间的函数关系如图所示.
根据以上信息,解决下列问题:
(1)求两种销售模式分别对应的函数表达式;
(2)求出图中点C的坐标,并说明其实际意义;
(3)若想购买10千克威宁芸豆,请问选择哪种模式购买更省钱?
18.如图为一位旅行者在早晨8时从城市出发到郊外所走的路程S(单位:千米)与时间t(单位:时)的变量关系的图象.根据图象回答问题:
(1)在这个变化过程中,自变量是 ,因变量是 .
(2)9时,10时,12时所走的路程分别是多少?
(3)他休息了多长时间?
(4)他从休息后直至到达目的地这段时间的平均速度是多少?
19.如图,在平面直角坐标系中,点的坐标为,点的坐标为,点的坐标为.
(1)在图中作出关于轴对称的.(2)请直接写出点,,的坐标.(3)求的面积.
20.(1)在平面直角坐标系中,画,使其三个顶点为,,;
(2)是直角三角形吗?请证明你的判断.
21.已知点,根据条件,解决下列问题:
(1)点A的横坐标是纵坐标的3倍,求点A的坐标;
(2)点A在过点且与x轴平行的直线上,求线段AP的长.
22.小明同学骑自行车去郊外春游,骑行个小时后,自行车出现损坏,维修好后继续骑行,如图表示他离家的距离(千米)与所用的时间(小时)之间关系的图象.
(1)根据图象回答:小明在离家最远的地方停留了多久?此时离家多远?
(2)求小明出发两个半小时离家多远?
(3)求小明出发多长时间距家千米?
参考答案:
1.C
【详解】解:∵小明的家在学校正南,正东方向处,如果以学校位置为原点,以正北、正东为正方向,
∴小明家用有序数对表示为,
故选:C.
2.B
【详解】解: 用有序数对表示点的平移,得到的数为1,得到的数为3,
数轴上的数向左边平移个单位得到的数为
数轴上的数向右边平移个单位得到的数为
可表示数轴上的数向左边平移个单位得到的数是
故选:
3.A
【详解】解:由图可得:
点B的坐标为,
故选A.
4.A
【详解】解:∵点P在第三象限,且点P到x轴和y轴的距离分别为8,5,
∴点P的横坐标是,纵坐标是,即点P的坐标为.
故选:A.
5.C
【详解】解:∵,
∴点P的纵坐标、横坐标之和为5,大于0,
∵第三象限的点的横坐标是负数,纵坐标是负数,
∴纵坐标、横坐标之和必然小于0,
∴点P一定不在第三象限,
故选:C.
6.C
【详解】解:由题意得:,
解得:,
∴整数m的值为3,
故选:C.
7.C
【详解】解:由题意得:
∴坐标原点为点P,
故选:C.
8.C
【详解】解:如图所示,,,,
∵图上一个单位长度表示10米,
∴,
故选:C.
9.C
【详解】解:彤彤和妈妈最后跑步回家,因此最后的y值为0,排除A选项;
彤彤和妈妈在公园中央的休息区聊了会儿天,因此中间有一段时间y值不变,排除D选项;
彤彤和妈妈散步到公园,再从公园跑步回家,因此回家用时较少,排除B选项,
故选C.
10.D
【详解】解:由图可得,甲乙出发后0.5h相遇,故A正确,不符合题意;
乙步行的速度为:(km/h),
则甲骑车的速度为:(km/h),故B正确,不符合题意;
两人相遇地点与A地的距离为:(km),故C正确,不符合题意;
设线段对应的与x的函数关系式是,
∵点在函数的图象上,
∴,
解得,
即线段对应的y甲与x的函数关系式是;
设与x的函数关系式是,
∵点在函数的图象上,
∴,解得,
即与x的函数关系式是,
令,
解得,
即经过小时或小时,甲、乙两人相距,故D错误,符合题意;
故选:D.
11.B
【详解】解:设的半径为r,李老师跑步的速度为v,
当时,;
当时,,
当时,.
故选:B.
12.C
【详解】解:由题意可知,第1次从原点运动到点,
第2次接着运动到点,
第3次接着运动到点,
第4次从原点运动到点,
第5次接着运动到点,
第6次接着运动到点,
……
第次接着运动到点,
第次接着运动到点,
第次从原点运动到点,
第次接着运动到点,
∵,
∴第2023次接着运动到点,
故选C.
13.3或
【详解】解:若点P在x轴上,则,
解得,
若点P在y轴上,则,
解得,
所以或.
故答案为:3或.
14.
【详解】解:设甲的速度为米分,乙的速度为米分,由图象可得,
,
解得:,
设则相遇地点到的距离为()米,由题意得,
,
解得,,
故答案为:.
15.
【详解】解:∵轴,,,
∴,解得,
故答案为:.
16.
【详解】解:由图形得出从开始,点的横坐标依次是0、1、2、3、4、…、n,纵坐标依次是2、0、、0、2、0、、…,四个为一组,
∴的横坐标为2023,
,
∴的纵坐标为,
∴的坐标为,
故答案为:.
17.(1)线下:,线上:(2),见解析;(3)选择线上购买更省钱
【详解】(1)解:线下销售:.
线上销售:当时,;
当时,.
故线下销售y与x之间的函数表达式为,
线上销售y与x之间的函数表达式为
(2)由题意,知图中射线为线下销售,折线为线上销售.
由图象,得,解得,
∴,
∴,
∴图中点C的实际意义为:当购买9千克威宁荟豆时,线上线下所花的钱数相同,都为36元.
(3)根据图象,可知当时,选择线上购买更省钱.
∴购买10千克威宁芸豆,选择线上购买更省钱.
18.(1)时间,路程;(2)9时,10时,12时所走的路程分别是,,;(3)1小时;(4)
【详解】(1)解:由图象可得,时间是自变量,路程是因变量;
故答案为:时间;路程;
(2)由图可知:9时,10时,12时所走的路程分别是,,;
(3)根据图象可得,该旅行者休息的时间为:小时;
(4)根据图象得:.
即他从休息后直至到达目的地这段时间的平均速度是.
19.(1)作图详见解析;(2),,;(3)
【详解】(1)解:如图所示,即为所作.
(2)如图,可得点,,的坐标,即:,,.
(3)的面积是:.
∴的面积为.
20.(1)见解析;(2)是直角三角形;理由见解析
【详解】(1)
(2)是直角三角形.
理由如下:
由勾股定理可知,,,
∵,
∴,
∴是直角三角形.
21.(1);(2)
【详解】(1)解:∵点A的横坐标是纵坐标的3倍,
∴,解得:,
∴,
∴;
(2)解:∵点A在过点且与x轴平行的直线上,
∴,
∴,
∴,
∴,
∴.
22.(1)小明在离家最远的地方停留了小时,此时离家千米;(2)小明出发两个半小时离家千米;
(3)小明出发小时与小时时,小明距家千米
【详解】(1)根据图象,小明在离家最远的地方停留了小时,此时离家千米.
(2)段表示的速度为千米/时,
(千米).
即小明出发两个半小时离家千米.
(3)段表示的速度为(千米/时),
(小时),
段表示的速度为(千米/时),
(小时),
即当小明出发小时与小时时,小明距家千米.
学校:___________姓名:___________班级:___________考号:___________
一、单选题(每小题4分,共48分)
1.小明的家在学校正南,正东方向处,如果以学校位置为原点,以正东、正北为正方向,则小明家用有序数对表示为( )
A. B. C. D.
2.在数轴上,用有序数对表示点的平移,若得到的数为1,得到的数为3,则得到的数为( ).
A.8 B. C.2 D.
3.在如图所示的平面直角坐标系中,点B的坐标为( )
A. B. C. D.
4.在平面直角坐标系中,点在第三象限,且Р到x轴和y轴的距离分别为8和5,则点P的坐标为( )
A. B. C. D.
5.不论m取何实数,点都不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.在平面直角坐标系中,若点在第二象限,则整数m的值为( )
A.1 B.2 C.3 D.4
7.如图,在某平面直角坐标系的网格中,点A的坐标为,点C的坐标为,则它的坐标原点为( )
A.点B B.点D C.点P D.点Q
8.如图是一块不规则的四边形地皮,各顶点坐标分别为,,,(图上一个单位长度表示10米),则这块地皮的面积是( ).
A.25 B.250 C.2500 D.2200
9.晚饭后彤彤和妈妈散步到小区旁边的公园,在公园中央的休息区聊了会儿天,然后一起跑步回家,下面能反映肜彤和妈妈离家的距离y与时间x的函数关系的大致图象是( )
A.B.C. D.
10.A、B两地相距12km,甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图所示的折线和线段EF分别表示甲、乙两人与A地的距离y(km)与时间x(h)之间的函数关系,且OP与EF交于点G.下列说法中错误的是( )
A.甲乙出发后0.5h相遇 B.甲骑自行车的速度为
C.两人相遇地点与A地的距离为9km D.甲、乙相距3km时,出发时间为
11.如图,李老师早晨出门去锻炼,一段时间内沿的半圆形路径匀速慢跑,那么李老师离出发点M的距离与时间之间的函数关系的大致图象是( )
A.B.C. D.
12.如图,动点P按图中箭头所示方向运动,第1次从原点运动到点,第2次运动到点,第3次运动到点,…,按这样的运动规律,则第2023次运动到点( )
A. B. C. D.
二、填空题(每小题4分,共16分)
13.已知在坐标轴上,则_____.
14.A、B、C三地依次在同一直线上,甲、乙两人同时从A地出发前往C地,已知当甲行走到B地时发现有重要物品放在乙处,于是甲立即返回与乙相遇,相遇以后甲、乙继续前往C地,最终甲比乙提前8分钟到达C地.若中途停留的时间忽略不计,且在整个行走过程中,甲、乙均保持各自速度匀速行走,甲、乙两人之间的距离y(米)与乙行走的时间x(分钟)之间的函数关系如图,则BC两地的距离为___________米.
15.已知点A,B的坐标分别为和,若轴,则___________.
16.如图,点,,,,…….根据这个规律,探究可得点的坐标是___________.
三、解答题(6个小题,共56分)
17.毕节某合作社为尽快打开市场,对威宁芸豆进行线上和线下销售相结合的模式,具体销售模式如下:
线下销售模式,标价5元/千克,八折出售;
线上销售模式:标价5元/千克,九折出售,超过6千克的,超出部分每千克再让利元.
设购买威宁芸豆x千克,所需费用为y元,y与x之间的函数关系如图所示.
根据以上信息,解决下列问题:
(1)求两种销售模式分别对应的函数表达式;
(2)求出图中点C的坐标,并说明其实际意义;
(3)若想购买10千克威宁芸豆,请问选择哪种模式购买更省钱?
18.如图为一位旅行者在早晨8时从城市出发到郊外所走的路程S(单位:千米)与时间t(单位:时)的变量关系的图象.根据图象回答问题:
(1)在这个变化过程中,自变量是 ,因变量是 .
(2)9时,10时,12时所走的路程分别是多少?
(3)他休息了多长时间?
(4)他从休息后直至到达目的地这段时间的平均速度是多少?
19.如图,在平面直角坐标系中,点的坐标为,点的坐标为,点的坐标为.
(1)在图中作出关于轴对称的.(2)请直接写出点,,的坐标.(3)求的面积.
20.(1)在平面直角坐标系中,画,使其三个顶点为,,;
(2)是直角三角形吗?请证明你的判断.
21.已知点,根据条件,解决下列问题:
(1)点A的横坐标是纵坐标的3倍,求点A的坐标;
(2)点A在过点且与x轴平行的直线上,求线段AP的长.
22.小明同学骑自行车去郊外春游,骑行个小时后,自行车出现损坏,维修好后继续骑行,如图表示他离家的距离(千米)与所用的时间(小时)之间关系的图象.
(1)根据图象回答:小明在离家最远的地方停留了多久?此时离家多远?
(2)求小明出发两个半小时离家多远?
(3)求小明出发多长时间距家千米?
参考答案:
1.C
【详解】解:∵小明的家在学校正南,正东方向处,如果以学校位置为原点,以正北、正东为正方向,
∴小明家用有序数对表示为,
故选:C.
2.B
【详解】解: 用有序数对表示点的平移,得到的数为1,得到的数为3,
数轴上的数向左边平移个单位得到的数为
数轴上的数向右边平移个单位得到的数为
可表示数轴上的数向左边平移个单位得到的数是
故选:
3.A
【详解】解:由图可得:
点B的坐标为,
故选A.
4.A
【详解】解:∵点P在第三象限,且点P到x轴和y轴的距离分别为8,5,
∴点P的横坐标是,纵坐标是,即点P的坐标为.
故选:A.
5.C
【详解】解:∵,
∴点P的纵坐标、横坐标之和为5,大于0,
∵第三象限的点的横坐标是负数,纵坐标是负数,
∴纵坐标、横坐标之和必然小于0,
∴点P一定不在第三象限,
故选:C.
6.C
【详解】解:由题意得:,
解得:,
∴整数m的值为3,
故选:C.
7.C
【详解】解:由题意得:
∴坐标原点为点P,
故选:C.
8.C
【详解】解:如图所示,,,,
∵图上一个单位长度表示10米,
∴,
故选:C.
9.C
【详解】解:彤彤和妈妈最后跑步回家,因此最后的y值为0,排除A选项;
彤彤和妈妈在公园中央的休息区聊了会儿天,因此中间有一段时间y值不变,排除D选项;
彤彤和妈妈散步到公园,再从公园跑步回家,因此回家用时较少,排除B选项,
故选C.
10.D
【详解】解:由图可得,甲乙出发后0.5h相遇,故A正确,不符合题意;
乙步行的速度为:(km/h),
则甲骑车的速度为:(km/h),故B正确,不符合题意;
两人相遇地点与A地的距离为:(km),故C正确,不符合题意;
设线段对应的与x的函数关系式是,
∵点在函数的图象上,
∴,
解得,
即线段对应的y甲与x的函数关系式是;
设与x的函数关系式是,
∵点在函数的图象上,
∴,解得,
即与x的函数关系式是,
令,
解得,
即经过小时或小时,甲、乙两人相距,故D错误,符合题意;
故选:D.
11.B
【详解】解:设的半径为r,李老师跑步的速度为v,
当时,;
当时,,
当时,.
故选:B.
12.C
【详解】解:由题意可知,第1次从原点运动到点,
第2次接着运动到点,
第3次接着运动到点,
第4次从原点运动到点,
第5次接着运动到点,
第6次接着运动到点,
……
第次接着运动到点,
第次接着运动到点,
第次从原点运动到点,
第次接着运动到点,
∵,
∴第2023次接着运动到点,
故选C.
13.3或
【详解】解:若点P在x轴上,则,
解得,
若点P在y轴上,则,
解得,
所以或.
故答案为:3或.
14.
【详解】解:设甲的速度为米分,乙的速度为米分,由图象可得,
,
解得:,
设则相遇地点到的距离为()米,由题意得,
,
解得,,
故答案为:.
15.
【详解】解:∵轴,,,
∴,解得,
故答案为:.
16.
【详解】解:由图形得出从开始,点的横坐标依次是0、1、2、3、4、…、n,纵坐标依次是2、0、、0、2、0、、…,四个为一组,
∴的横坐标为2023,
,
∴的纵坐标为,
∴的坐标为,
故答案为:.
17.(1)线下:,线上:(2),见解析;(3)选择线上购买更省钱
【详解】(1)解:线下销售:.
线上销售:当时,;
当时,.
故线下销售y与x之间的函数表达式为,
线上销售y与x之间的函数表达式为
(2)由题意,知图中射线为线下销售,折线为线上销售.
由图象,得,解得,
∴,
∴,
∴图中点C的实际意义为:当购买9千克威宁荟豆时,线上线下所花的钱数相同,都为36元.
(3)根据图象,可知当时,选择线上购买更省钱.
∴购买10千克威宁芸豆,选择线上购买更省钱.
18.(1)时间,路程;(2)9时,10时,12时所走的路程分别是,,;(3)1小时;(4)
【详解】(1)解:由图象可得,时间是自变量,路程是因变量;
故答案为:时间;路程;
(2)由图可知:9时,10时,12时所走的路程分别是,,;
(3)根据图象可得,该旅行者休息的时间为:小时;
(4)根据图象得:.
即他从休息后直至到达目的地这段时间的平均速度是.
19.(1)作图详见解析;(2),,;(3)
【详解】(1)解:如图所示,即为所作.
(2)如图,可得点,,的坐标,即:,,.
(3)的面积是:.
∴的面积为.
20.(1)见解析;(2)是直角三角形;理由见解析
【详解】(1)
(2)是直角三角形.
理由如下:
由勾股定理可知,,,
∵,
∴,
∴是直角三角形.
21.(1);(2)
【详解】(1)解:∵点A的横坐标是纵坐标的3倍,
∴,解得:,
∴,
∴;
(2)解:∵点A在过点且与x轴平行的直线上,
∴,
∴,
∴,
∴,
∴.
22.(1)小明在离家最远的地方停留了小时,此时离家千米;(2)小明出发两个半小时离家千米;
(3)小明出发小时与小时时,小明距家千米
【详解】(1)根据图象,小明在离家最远的地方停留了小时,此时离家千米.
(2)段表示的速度为千米/时,
(千米).
即小明出发两个半小时离家千米.
(3)段表示的速度为(千米/时),
(小时),
段表示的速度为(千米/时),
(小时),
即当小明出发小时与小时时,小明距家千米.
