2022-2023学年冀教版九年级数学下册 29.1 点与圆的位置关系 课后强化(无答案)
文档属性
| 名称 | 2022-2023学年冀教版九年级数学下册 29.1 点与圆的位置关系 课后强化(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 210.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 08:50:00 | ||
图片预览


文档简介
29.1点与圆的位置关系课后强化
班级:________ 姓名:________
一、单选题(共 8 小题)
1、如图,中,是内部的一个动点,且满足,则线段长的最小值为()
A.1 B.1.6 C. D.2
2、若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为( )
A. B. C. D.—1
3、如图所示,在4×4的网格中,A、B、C、D、O均在格点上,则点O是( )
A.△ABC的内心 B.△ABC的外心 C.△ACD的外心 D.△ACD的重心
4、下列语句中,正确的有( )
①相等的圆心角所对的弧相等;
②等弦对等弧;
③若两个相似多边形的面积比为16:9,那么这两个相似多边形的周长比是4:3;
④已知线段AB=2,点C是AB的黄全分割点,则;
⑤三角形的外心到三角形的三边距离相等.
A.1个 B.2个 C.3个 D.4个
5、如图,在△ABC中,AB=AC,BC=4,tanB=2,以AB的中点D为圆心,r为半径作⊙D,如果点B在⊙D内,点C在⊙D外,那么r可以取( )
A.2 B.3 C.4 D.5
6、已知⊙O的半径为8 cm,A为线段OP的中点,且OP=16 cm,则点A与⊙O的位置关系是 ( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
7、如图,已知直线与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最小值为( )
A.5.5 B.10.5 C.8 D.12
8、已知AB=12 cm,过A,B两点画半径为8 cm的圆,则能画的圆的个数为( )
A.0个 B.1个 C.2个 D.无数个
二、填空题(共 8 小题)
1、若的半径为,圆心O为坐标系的原点,点P的坐标是,点P在______.
2、如图,已知的半径是4,点A,B在上,且,动点C在上运动(不与A,B重合),点D为线段的中点,连接,则线段长度的最值是 _____.
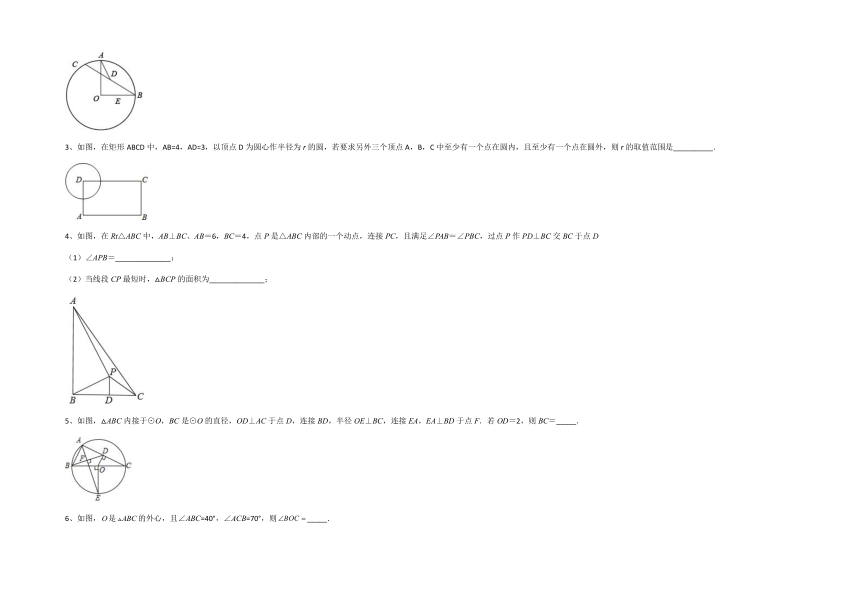
3、如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是__________.
4、如图,在Rt△ABC中,AB⊥BC、AB=6,BC=4,点P是△ABC内部的一个动点,连接PC,且满足∠PAB=∠PBC,过点P作PD⊥BC交BC于点D
(1)∠APB=______________;
(2)当线段CP最短时,△BCP的面积为______________;
5、如图,△ABC内接于⊙O,BC是⊙O的直径,OD⊥AC于点D,连接BD,半径OE⊥BC,连接EA,EA⊥BD于点F.若OD=2,则BC=_____.
6、如图,是的外心,且∠ABC=40°,∠ACB=70°,则_____.
7、矩形 中,边 , ,以A为圆心作 ,使B、C、D三点有两个点在内,有一点在外,则的半径的取值范围是____.
8、已知正ABC的边长为6,那么能够完全覆盖这个正ABC的最小圆的半径是_____.
三、解答题(共 5 小题)
1、如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;
(2)点M的坐标为 ;
(3)判断点D(5,﹣2)与⊙M的位置关系.
2、如图,已知平面直角坐标系中.,,.
(1)写出经过,,三点的圆弧所在圆的圆心的坐标:(______,______);
(2)判断点与的位置关系,写出解题过程.
3、在直角坐标平面内,三个顶点的坐标分别为、、(正方形网格中每个小正方形的边长是一个单位长度).
(1)将向下平移4个单位长度得到的,则点的坐标是____________;
(2)以点B为位似中心,在网格上画出,使与位似,且位似比为2:1,求点的坐标;
(3)若是外接圆,求的半径.
4、操作与计算:
(1)用尺规作出△ABC的外接圆⊙O(保留作图痕迹,不写作法);
(2)若AB=AC=5,BC=6,求⊙O的半径.
5、如图所示,已知△ABC中,∠C=90°,AC=3,BC=4,M为AB的中点.
(1)以C为圆心,3为半径作⊙C,则点A、B、M与⊙C的位置关系如何
(2)若以C为圆心,作⊙C,使A、M两点在⊙A内且B点在⊙C外,求⊙C的半径r的取值范围.
班级:________ 姓名:________
一、单选题(共 8 小题)
1、如图,中,是内部的一个动点,且满足,则线段长的最小值为()
A.1 B.1.6 C. D.2
2、若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为( )
A. B. C. D.—1
3、如图所示,在4×4的网格中,A、B、C、D、O均在格点上,则点O是( )
A.△ABC的内心 B.△ABC的外心 C.△ACD的外心 D.△ACD的重心
4、下列语句中,正确的有( )
①相等的圆心角所对的弧相等;
②等弦对等弧;
③若两个相似多边形的面积比为16:9,那么这两个相似多边形的周长比是4:3;
④已知线段AB=2,点C是AB的黄全分割点,则;
⑤三角形的外心到三角形的三边距离相等.
A.1个 B.2个 C.3个 D.4个
5、如图,在△ABC中,AB=AC,BC=4,tanB=2,以AB的中点D为圆心,r为半径作⊙D,如果点B在⊙D内,点C在⊙D外,那么r可以取( )
A.2 B.3 C.4 D.5
6、已知⊙O的半径为8 cm,A为线段OP的中点,且OP=16 cm,则点A与⊙O的位置关系是 ( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
7、如图,已知直线与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最小值为( )
A.5.5 B.10.5 C.8 D.12
8、已知AB=12 cm,过A,B两点画半径为8 cm的圆,则能画的圆的个数为( )
A.0个 B.1个 C.2个 D.无数个
二、填空题(共 8 小题)
1、若的半径为,圆心O为坐标系的原点,点P的坐标是,点P在______.
2、如图,已知的半径是4,点A,B在上,且,动点C在上运动(不与A,B重合),点D为线段的中点,连接,则线段长度的最值是 _____.
3、如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是__________.
4、如图,在Rt△ABC中,AB⊥BC、AB=6,BC=4,点P是△ABC内部的一个动点,连接PC,且满足∠PAB=∠PBC,过点P作PD⊥BC交BC于点D
(1)∠APB=______________;
(2)当线段CP最短时,△BCP的面积为______________;
5、如图,△ABC内接于⊙O,BC是⊙O的直径,OD⊥AC于点D,连接BD,半径OE⊥BC,连接EA,EA⊥BD于点F.若OD=2,则BC=_____.
6、如图,是的外心,且∠ABC=40°,∠ACB=70°,则_____.
7、矩形 中,边 , ,以A为圆心作 ,使B、C、D三点有两个点在内,有一点在外,则的半径的取值范围是____.
8、已知正ABC的边长为6,那么能够完全覆盖这个正ABC的最小圆的半径是_____.
三、解答题(共 5 小题)
1、如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;
(2)点M的坐标为 ;
(3)判断点D(5,﹣2)与⊙M的位置关系.
2、如图,已知平面直角坐标系中.,,.
(1)写出经过,,三点的圆弧所在圆的圆心的坐标:(______,______);
(2)判断点与的位置关系,写出解题过程.
3、在直角坐标平面内,三个顶点的坐标分别为、、(正方形网格中每个小正方形的边长是一个单位长度).
(1)将向下平移4个单位长度得到的,则点的坐标是____________;
(2)以点B为位似中心,在网格上画出,使与位似,且位似比为2:1,求点的坐标;
(3)若是外接圆,求的半径.
4、操作与计算:
(1)用尺规作出△ABC的外接圆⊙O(保留作图痕迹,不写作法);
(2)若AB=AC=5,BC=6,求⊙O的半径.
5、如图所示,已知△ABC中,∠C=90°,AC=3,BC=4,M为AB的中点.
(1)以C为圆心,3为半径作⊙C,则点A、B、M与⊙C的位置关系如何
(2)若以C为圆心,作⊙C,使A、M两点在⊙A内且B点在⊙C外,求⊙C的半径r的取值范围.
