山西省朔州市应县一中2013-2014学年高二第六次月考数学(文)试题
文档属性
| 名称 | 山西省朔州市应县一中2013-2014学年高二第六次月考数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 167.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-08 20:01:59 | ||
图片预览

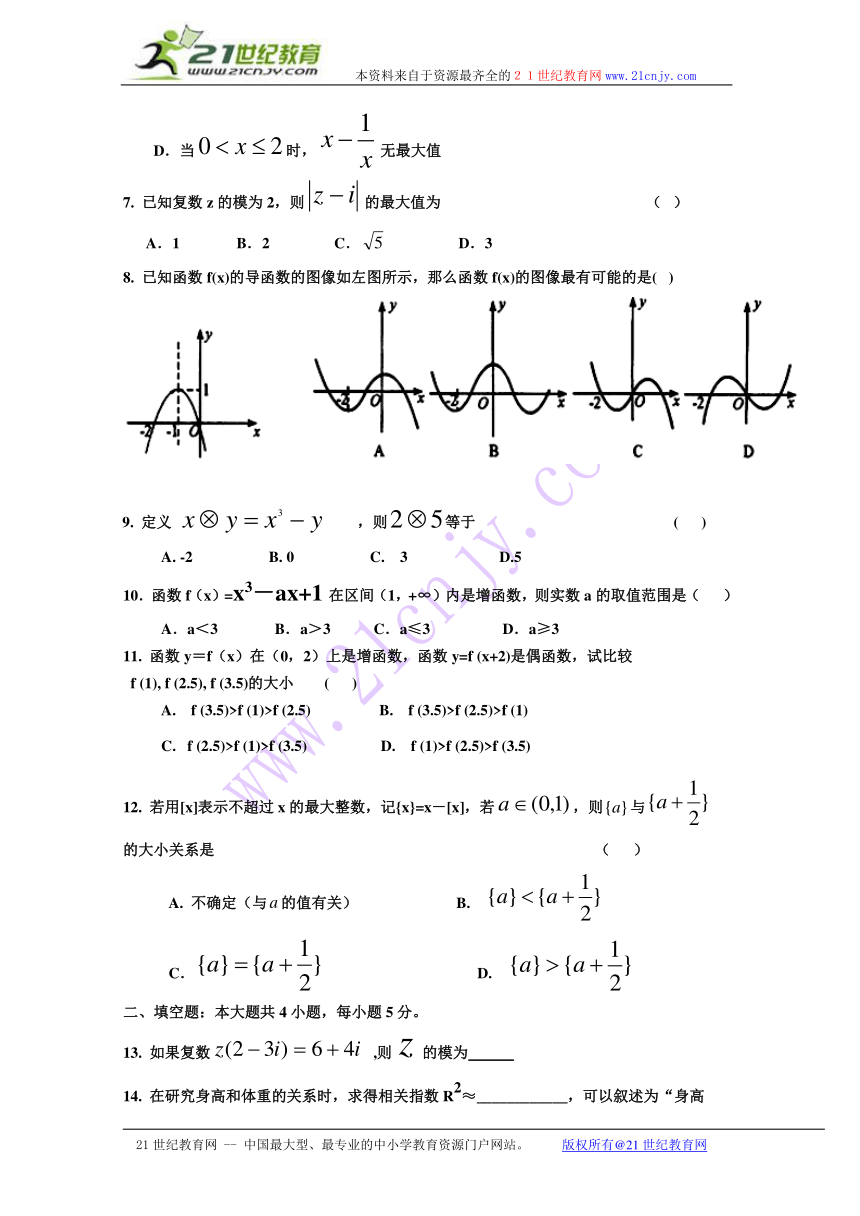

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
应县一中2013-2014学年高二第六次月考
数学文试题
时间:120分钟 满分:150分
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一个是符合题目要求的。
1. 化简复数 = ( )
A.i B. -i C.2 D.2i
2.设,且,则 ( )
A. B. C. D.
3. 一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归模型为
= 7.19 x +73.93. 用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )21·世纪*教育网
A.身高一定是145.83 cm; B.身高在145.83 cm以上;
C.身高在145.83 cm以下; D.身高在145.83 cm左右.
4. 曲线f(x)=x3+x-2的一条切线平行于直线y=4x-1,则切点P0的坐标为( )
A.(0,-1)或(1,0) B.(1,0)或(-1,-4)
C.(-1,-4)或(0,-2) D.(1,0)或(2,8)
5. 有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线
∥平面,直线,则直线∥直线” 结论显然是错误的,这是因为( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
6. 下列说法中,正确的是 ( )
A. 当且时,
B.当时,
C.当时,的最小值为2
D.当时,无最大值
7. 已知复数z的模为2,则的最大值为 ( )
A.1 B.2 C. D.321·cn·jy·com
8. 已知函数f(x)的导函数的图像如左图所示,那么函数f(x)的图像最有可能的是( )
( http: / / www.21cnjy.com )
9. 定义 ,则等于 ( )
A. -2 B. 0 C. 3 D.5
10.函数f(x)=x3-ax+1在区间(1,+∞)内是增函数,则实数a的取值范围是( )
A.a<3 B.a>3 C.a≤3 D.a≥3
11. 函数y=f(x)在(0,2)上是增函数,函数y=f (x+2)是偶函数,试比较
f (1), f (2.5), f (3.5)的大小 ( )
A. f (3.5)>f (1)>f (2.5) B. f (3.5)>f (2.5)>f (1) 21cnjy.com
C. f (2.5)>f (1)>f (3.5) D. f (1)>f (2.5)>f (3.5)2·1·c·n·j·y
12. 若用[x]表示不超过x的最大整数,记{x}=x-[x],若,则与
的大小关系是 ( )
A. 不确定(与的值有关) B.
C. D.
二、填空题:本大题共4小题,每小题5分。
13. 如果复数 ,则的模为
14. 在研究身高和体重的关系时,求得相关指数R2≈____________,可以叙述为“身高
解释了64%的体重变化,而随机误差贡献了剩余的36%”所以身高对体重的效应比随机误
差的效应大得多。
15. 某少数民族的刺绣有着悠久的历史,如 ( http: / / www.21cnjy.com )下图所示为她们刺绣最简单的三个图案,这些图 案都是由小圆构成,小圆数越多刺绣越漂亮.现按同样的规律刺绣(小圆的摆放规律相同),设第n个图形包含f(n)个小圆.则f (5)的值为 .www.21-cn-jy.com
( http: / / www.21cnjy.com )
16. 设,不等式对恒成立,则的取值范围为
三、解答题:解答应写出文字说明,证明过程或演算步骤。
17. (本小题满分10分)
用适当方法证明:已知,求证:
18. (本小题满分12分)
设 , ,当为何值时, 是:
(1)零;
(2)纯虚数;
(3)复平面内第二、四象限角平分线上的点对应的复数?
19. (本小题满分12分)
如图:正方形ABCD和四边形ACEF所在的平面互相垂直,EF∥AC,AB= ( http: / / www.21cnjy.com ) . CE=EF=1.【来源:21·世纪·教育·网】
(1) 求证:AF∥平面BDE.
(2) 求证:CF⊥平面BDE
20. (本小题满分12分)
已知:在上是减函数,解关于的不等式:
21. (本小题满分12分)
已知数列{an}的首项=,= , 1,2,…
(1)证明:数列{}是等比数列;
(2)求数列{}的前项和.
22. (本小题满分12分)
设函数f(x)=x3+ax2-a2x+1 ,g(x)=ax2-2x+1 ,其中实数a≠0 。
(1)若a>0求函数f(x)的单调区间;
(2)若f(x)与g(x)在区间(a , a+2)内均为增函数,求a 的取值范围。
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
22. 解析:(1)∵f/(x)=3x2+2ax-a2=3(x-)(x+a),
∵a>0 ,∴当x<-a 或x> 时,f/(x)>0; 当-a∴f(x)在(-∞ ,-a)和 ( ,+∞)内是增函数,在(-a ,)内是减函数
(2)当a>0时,f(x)在(-∞ ,-a)和 ( ,+∞)内是增函数 ,g(x)在()内是增函数21世纪教育网版权所有
∴ 解得
当a<0时,f(x)在(-∞ ,)和 (-a,+∞)内是增函数 ,g(x)在(-∞ ,)内是增函数21教育网
∴ 解得
综上可知,a 的取值范围为
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
应县一中2013-2014学年高二第六次月考
数学文试题
时间:120分钟 满分:150分
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一个是符合题目要求的。
1. 化简复数 = ( )
A.i B. -i C.2 D.2i
2.设,且,则 ( )
A. B. C. D.
3. 一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归模型为
= 7.19 x +73.93. 用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )21·世纪*教育网
A.身高一定是145.83 cm; B.身高在145.83 cm以上;
C.身高在145.83 cm以下; D.身高在145.83 cm左右.
4. 曲线f(x)=x3+x-2的一条切线平行于直线y=4x-1,则切点P0的坐标为( )
A.(0,-1)或(1,0) B.(1,0)或(-1,-4)
C.(-1,-4)或(0,-2) D.(1,0)或(2,8)
5. 有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线
∥平面,直线,则直线∥直线” 结论显然是错误的,这是因为( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
6. 下列说法中,正确的是 ( )
A. 当且时,
B.当时,
C.当时,的最小值为2
D.当时,无最大值
7. 已知复数z的模为2,则的最大值为 ( )
A.1 B.2 C. D.321·cn·jy·com
8. 已知函数f(x)的导函数的图像如左图所示,那么函数f(x)的图像最有可能的是( )
( http: / / www.21cnjy.com )
9. 定义 ,则等于 ( )
A. -2 B. 0 C. 3 D.5
10.函数f(x)=x3-ax+1在区间(1,+∞)内是增函数,则实数a的取值范围是( )
A.a<3 B.a>3 C.a≤3 D.a≥3
11. 函数y=f(x)在(0,2)上是增函数,函数y=f (x+2)是偶函数,试比较
f (1), f (2.5), f (3.5)的大小 ( )
A. f (3.5)>f (1)>f (2.5) B. f (3.5)>f (2.5)>f (1) 21cnjy.com
C. f (2.5)>f (1)>f (3.5) D. f (1)>f (2.5)>f (3.5)2·1·c·n·j·y
12. 若用[x]表示不超过x的最大整数,记{x}=x-[x],若,则与
的大小关系是 ( )
A. 不确定(与的值有关) B.
C. D.
二、填空题:本大题共4小题,每小题5分。
13. 如果复数 ,则的模为
14. 在研究身高和体重的关系时,求得相关指数R2≈____________,可以叙述为“身高
解释了64%的体重变化,而随机误差贡献了剩余的36%”所以身高对体重的效应比随机误
差的效应大得多。
15. 某少数民族的刺绣有着悠久的历史,如 ( http: / / www.21cnjy.com )下图所示为她们刺绣最简单的三个图案,这些图 案都是由小圆构成,小圆数越多刺绣越漂亮.现按同样的规律刺绣(小圆的摆放规律相同),设第n个图形包含f(n)个小圆.则f (5)的值为 .www.21-cn-jy.com
( http: / / www.21cnjy.com )
16. 设,不等式对恒成立,则的取值范围为
三、解答题:解答应写出文字说明,证明过程或演算步骤。
17. (本小题满分10分)
用适当方法证明:已知,求证:
18. (本小题满分12分)
设 , ,当为何值时, 是:
(1)零;
(2)纯虚数;
(3)复平面内第二、四象限角平分线上的点对应的复数?
19. (本小题满分12分)
如图:正方形ABCD和四边形ACEF所在的平面互相垂直,EF∥AC,AB= ( http: / / www.21cnjy.com ) . CE=EF=1.【来源:21·世纪·教育·网】
(1) 求证:AF∥平面BDE.
(2) 求证:CF⊥平面BDE
20. (本小题满分12分)
已知:在上是减函数,解关于的不等式:
21. (本小题满分12分)
已知数列{an}的首项=,= , 1,2,…
(1)证明:数列{}是等比数列;
(2)求数列{}的前项和.
22. (本小题满分12分)
设函数f(x)=x3+ax2-a2x+1 ,g(x)=ax2-2x+1 ,其中实数a≠0 。
(1)若a>0求函数f(x)的单调区间;
(2)若f(x)与g(x)在区间(a , a+2)内均为增函数,求a 的取值范围。
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
22. 解析:(1)∵f/(x)=3x2+2ax-a2=3(x-)(x+a),
∵a>0 ,∴当x<-a 或x> 时,f/(x)>0; 当-a
(2)当a>0时,f(x)在(-∞ ,-a)和 ( ,+∞)内是增函数 ,g(x)在()内是增函数21世纪教育网版权所有
∴ 解得
当a<0时,f(x)在(-∞ ,)和 (-a,+∞)内是增函数 ,g(x)在(-∞ ,)内是增函数21教育网
∴ 解得
综上可知,a 的取值范围为
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
