湘教版八年级数学下册2.6.2 菱形的判定 课件(共17张PPT)
文档属性
| 名称 | 湘教版八年级数学下册2.6.2 菱形的判定 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 713.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-04 00:00:00 | ||
图片预览

文档简介
(共17张PPT)
本课内容
本节内容
2.6.2
菱形的判定
湘教版数学 八年级下册
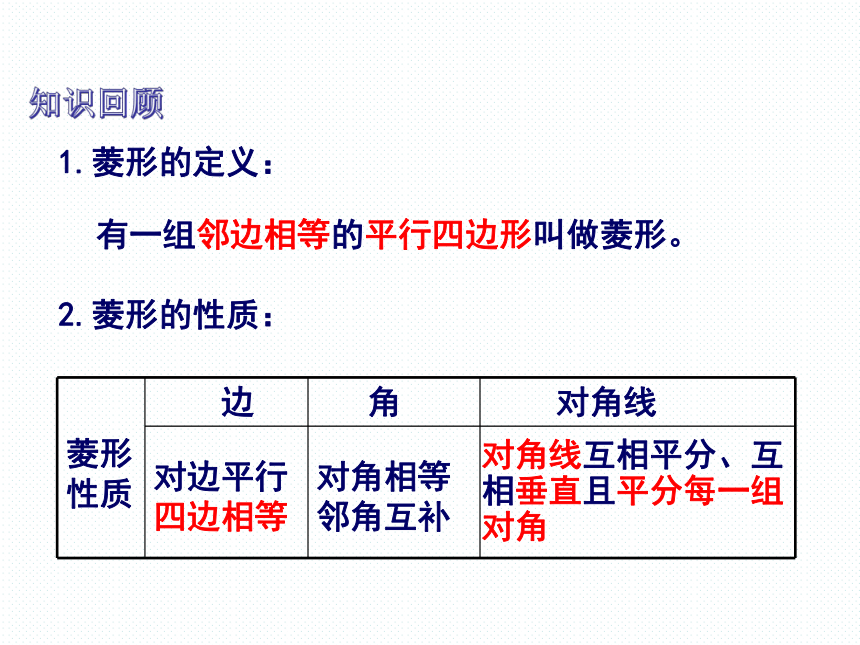
1.菱形的定义:
有一组邻边相等的平行四边形叫做菱形。
2.菱形的性质:
菱形性质 边 角 对角线
对边平行
四边相等
对角相等邻角互补
对角线互相平分、互相垂直且平分每一组对角
知识回顾
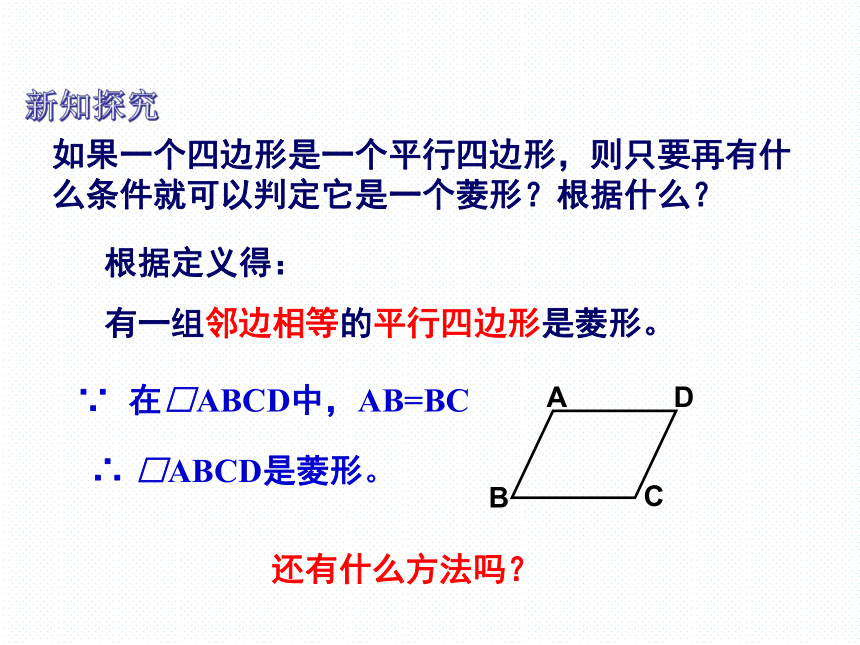
根据定义得:
有一组邻边相等的平行四边形是菱形。
A
B
C
D
∵ 在□ABCD中,AB=BC
∴ □ABCD是菱形。
如果一个四边形是一个平行四边形,则只要再有什么条件就可以判定它是一个菱形?根据什么?
还有什么方法吗?
新知探究
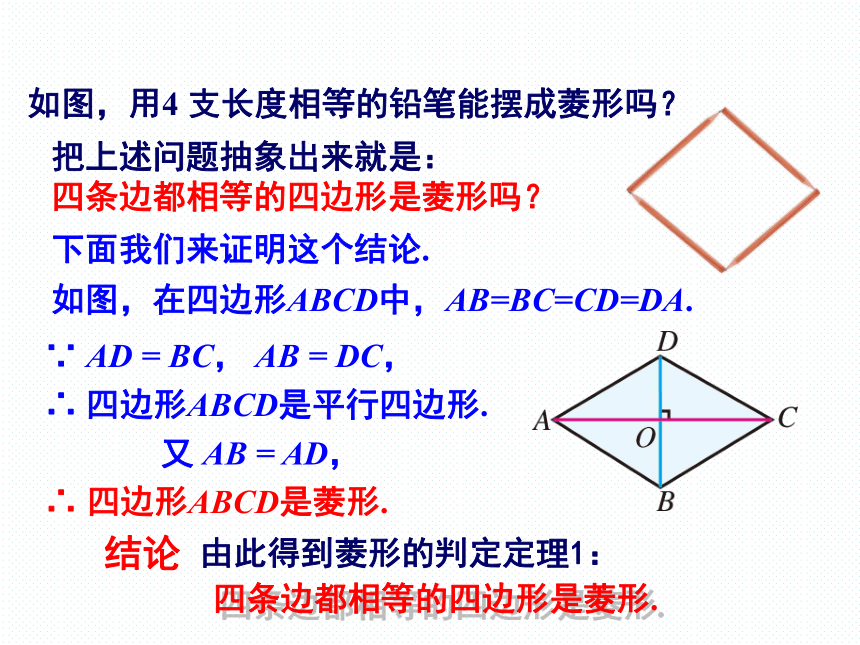
如图,用4 支长度相等的铅笔能摆成菱形吗?
把上述问题抽象出来就是:
四条边都相等的四边形是菱形吗?
下面我们来证明这个结论.
如图,在四边形ABCD中,AB=BC=CD=DA.
∵ AD = BC, AB = DC,
∴ 四边形ABCD是平行四边形.
又 AB = AD,
∴ 四边形ABCD是菱形.
四条边都相等的四边形是菱形.
由此得到菱形的判定定理1:
结论
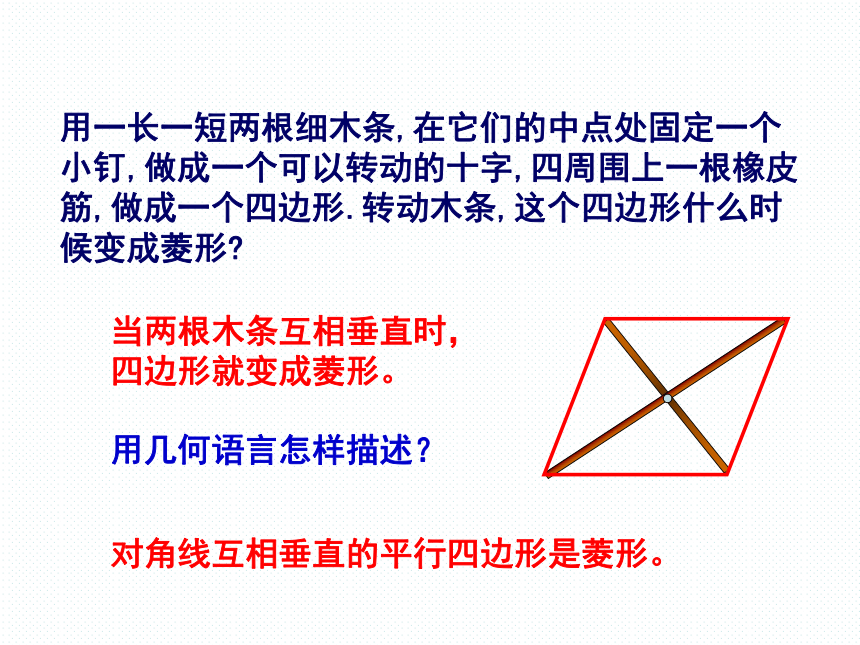
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形
当两根木条互相垂直时,四边形就变成菱形。
用几何语言怎样描述?
对角线互相垂直的平行四边形是菱形。
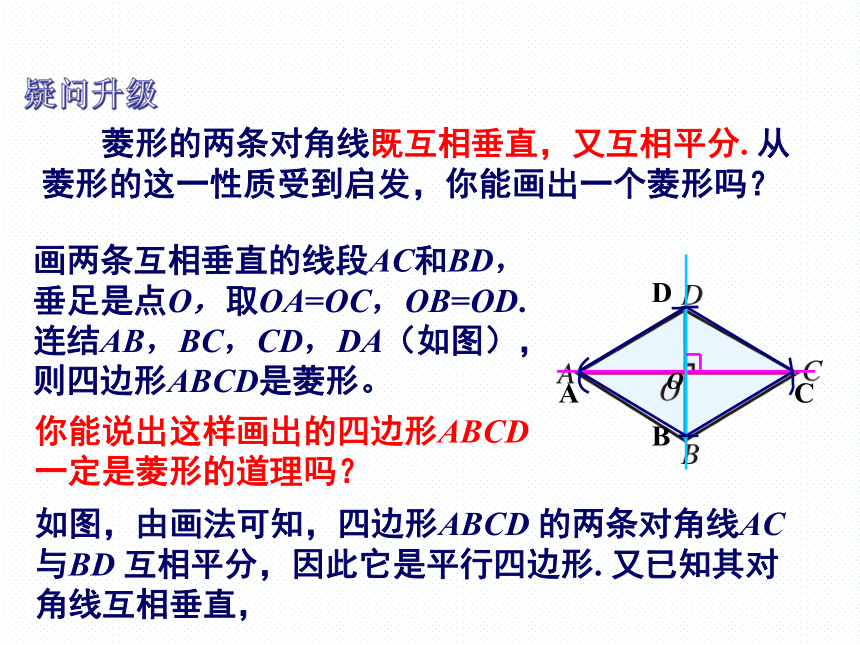
菱形的两条对角线既互相垂直,又互相平分. 从菱形的这一性质受到启发,你能画出一个菱形吗?
O
A
C
B
D
你能说出这样画出的四边形ABCD一定是菱形的道理吗?
画两条互相垂直的线段AC和BD,垂足是点O,取OA=OC,OB=OD. 连结AB,BC,CD,DA(如图),则四边形ABCD是菱形。
如图,由画法可知,四边形ABCD 的两条对角线AC 与BD 互相平分,因此它是平行四边形. 又已知其对角线互相垂直,
疑问升级
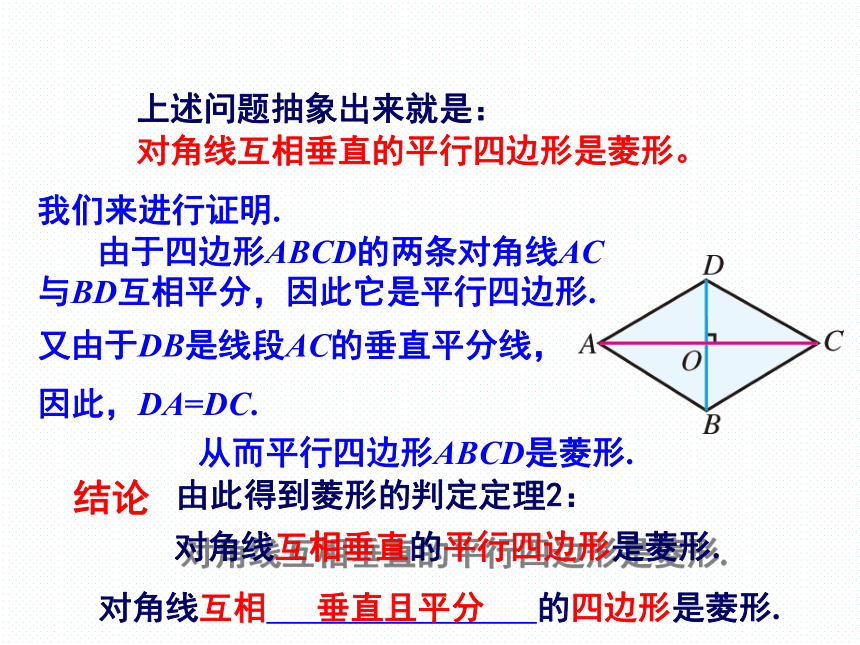
上述问题抽象出来就是:
对角线互相垂直的平行四边形是菱形。
我们来进行证明.
又由于DB是线段AC的垂直平分线,
由于四边形ABCD的两条对角线AC与BD互相平分,因此它是平行四边形.
因此,DA=DC.
从而平行四边形ABCD是菱形.
结论
由此得到菱形的判定定理2:
对角线互相垂直的平行四边形是菱形.
对角线互相 的四边形是菱形.
垂直且平分
例1.已知:如图,在四边形ABCD 中,线段BD
垂直平分AC,且相交于点O,∠1 =∠2.
求证:四边形ABCD是菱形.
提示: 由线段的垂直平分线,
得:BA=BC=DA=DC.
例2.如图,在平行四边形ABCD中,AC = 6,BD = 8,AD = 5. 求AB的长.
提示: 由勾股定理,得:△DAO是直角三角形.即:AC⊥BD
从而得:平行四边形ABCD是菱形.
∴ AB=AD=5 .
例题讲解
例3.如图,已知等腰△ABC中,AB=AC,AD平分∠BAC交BC于D点,在线段AD上任取一点P(A点除外),过P点作EF∥AB,分别交AC、BC于E、F点,作PM∥AC,交AB于M点,连结ME.
(1)求证:四边形AEPM为菱形.
(2)当P点在何处时,菱形AEPM的面积为四边EFBM面积的一半?
解:(1)∵EF∥AB,PM∥AC,
∴四边形AEPM为平行四边形.
∴四边形AEPM为菱形.
又∵ ∠BAD=∠EPA,
∴ ∠CAD=∠EPA,
∴EA=EP.
∵ AB=AC,AD平分∠CAB,
∴ ∠CAD=∠BAD,
解:(2)P为EF中点时,
N
∵四边形AEPM为菱形, ∴ AD⊥EM,∵AD⊥BC, ∴ EM∥BC.
又∵EF∥AB,∴四边形EFBM为平行四边形.
作EN ⊥ AB于N,
EP= EF
1
2
(2)当P点在何处时,菱形AEPM的面积为四边形EFBM面积的一半?
例4.如图,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB、BC、CD、DA的中点分别为P、Q、M、N,试判断四边形PQMN为
怎样的四边形.并证明你的结论.
证明:连结AC,BD.
∵ PQ为△ABC的中位线,
∴ 四边形PQMN为平行四边形.
在△AEC和△DEB中,AE=DE,EC=EB,
∠AEC=∠DEB= 180°- 60° = 120° ,
∴ △AEC≌△DEB.
∴ AC=DB. ∴ PQ=PN. ∴ □PQMN为菱形.
∴PQ AC
∥
=
2
1
同理 ∴MN PQ
MN AC
∥
=
2
1
∥
=
1.判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等 的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一组对角的四边形是菱形.
√
╳
╳
╳
2.菱形两条对角线长为6和8,菱形的边长为 ,
面积为 。
5
24
3.菱形的面积为96,对角线AC长为16 ,此菱形的边长为 。
10
随堂练习
4.菱形对角线的平方和等于一边平方的 ( )
A. 2倍 B. 3倍 C.4倍 D. 5倍
C
5.把两张等宽的纸条如图交叉重叠在一起,
则重叠部分ABCD的形状是( )
A.平行四边形 B.矩形
C.菱形 D.任意四边形
A
C
D
B
C
(1)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O 作MN⊥BD,分别交AD,BC于点M,N .求证:四边形BNDM是菱形.
6、解答题
提示:证明 △ODM≌△OBN.NB=MD.
又 MD∥BN,MN⊥BD,结论得证。
(2)如图,AD∥BC,BD垂直平分AC,四边形ABCD一定是菱形吗?若是,请说明理由。
C
D
B
A
O
┐
) 1
2 (
提示:△AOD≌△COB AD=BC
(3)已知:□ABCD 的对角线AC的垂直平分线与边AD 、BC分别交于E、F
求证:四边形AFCE是菱形。
分析: (1)利用定义判定
(2) 由已知可知
OA=OC,EF⊥AC.
(3)利用四边相等,你会吗?
(4)如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,证明:CE⊥DF.
A
B
F
N
D
M
E
C
提示:证明四边形DMNC是菱形
(5)已知:如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD、PC相交于点P。 (1)猜想:四边形PCOD是什么特殊的四边形?证明你的猜想。
(2)PO与CD有怎样的关系?
四边形PCOD是菱形。
PO⊥CD,且互相平分。
(6)如图,CD为Rt△ABC斜边AB上的高,∠BAC的平分线交CD于E,交BC于F,FG⊥AB于G.
求证:四边形EGFC为菱形.
G
F
E
D
C
B
A
(7)如图,Rt△ABC中,∠ACB=900,∠BAC=600,DE垂直平分BC,垂足为D,交AB于E,又点F在DE的延长线上,且AF=CE,求证:四边形ACEF是菱形。
F
E
D
C
B
A
易得:CE∥FG,再证△ACE≌ △AGE
∠B=∠ACD=∠AGE ,EG∥CF,
四边形EGFC是平行四边形,又CE=EG,
四边形EGFC为菱形.
AC=AF=EF=CE
菱形常用的判定方法:
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有四条边相等的四边形是菱形.
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
平行四边形
菱形
对角线互相垂直且平分
作业:P70 A 3、4、5 B 8
知识总结
本课内容
本节内容
2.6.2
菱形的判定
湘教版数学 八年级下册
1.菱形的定义:
有一组邻边相等的平行四边形叫做菱形。
2.菱形的性质:
菱形性质 边 角 对角线
对边平行
四边相等
对角相等邻角互补
对角线互相平分、互相垂直且平分每一组对角
知识回顾
根据定义得:
有一组邻边相等的平行四边形是菱形。
A
B
C
D
∵ 在□ABCD中,AB=BC
∴ □ABCD是菱形。
如果一个四边形是一个平行四边形,则只要再有什么条件就可以判定它是一个菱形?根据什么?
还有什么方法吗?
新知探究
如图,用4 支长度相等的铅笔能摆成菱形吗?
把上述问题抽象出来就是:
四条边都相等的四边形是菱形吗?
下面我们来证明这个结论.
如图,在四边形ABCD中,AB=BC=CD=DA.
∵ AD = BC, AB = DC,
∴ 四边形ABCD是平行四边形.
又 AB = AD,
∴ 四边形ABCD是菱形.
四条边都相等的四边形是菱形.
由此得到菱形的判定定理1:
结论
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形
当两根木条互相垂直时,四边形就变成菱形。
用几何语言怎样描述?
对角线互相垂直的平行四边形是菱形。
菱形的两条对角线既互相垂直,又互相平分. 从菱形的这一性质受到启发,你能画出一个菱形吗?
O
A
C
B
D
你能说出这样画出的四边形ABCD一定是菱形的道理吗?
画两条互相垂直的线段AC和BD,垂足是点O,取OA=OC,OB=OD. 连结AB,BC,CD,DA(如图),则四边形ABCD是菱形。
如图,由画法可知,四边形ABCD 的两条对角线AC 与BD 互相平分,因此它是平行四边形. 又已知其对角线互相垂直,
疑问升级
上述问题抽象出来就是:
对角线互相垂直的平行四边形是菱形。
我们来进行证明.
又由于DB是线段AC的垂直平分线,
由于四边形ABCD的两条对角线AC与BD互相平分,因此它是平行四边形.
因此,DA=DC.
从而平行四边形ABCD是菱形.
结论
由此得到菱形的判定定理2:
对角线互相垂直的平行四边形是菱形.
对角线互相 的四边形是菱形.
垂直且平分
例1.已知:如图,在四边形ABCD 中,线段BD
垂直平分AC,且相交于点O,∠1 =∠2.
求证:四边形ABCD是菱形.
提示: 由线段的垂直平分线,
得:BA=BC=DA=DC.
例2.如图,在平行四边形ABCD中,AC = 6,BD = 8,AD = 5. 求AB的长.
提示: 由勾股定理,得:△DAO是直角三角形.即:AC⊥BD
从而得:平行四边形ABCD是菱形.
∴ AB=AD=5 .
例题讲解
例3.如图,已知等腰△ABC中,AB=AC,AD平分∠BAC交BC于D点,在线段AD上任取一点P(A点除外),过P点作EF∥AB,分别交AC、BC于E、F点,作PM∥AC,交AB于M点,连结ME.
(1)求证:四边形AEPM为菱形.
(2)当P点在何处时,菱形AEPM的面积为四边EFBM面积的一半?
解:(1)∵EF∥AB,PM∥AC,
∴四边形AEPM为平行四边形.
∴四边形AEPM为菱形.
又∵ ∠BAD=∠EPA,
∴ ∠CAD=∠EPA,
∴EA=EP.
∵ AB=AC,AD平分∠CAB,
∴ ∠CAD=∠BAD,
解:(2)P为EF中点时,
N
∵四边形AEPM为菱形, ∴ AD⊥EM,∵AD⊥BC, ∴ EM∥BC.
又∵EF∥AB,∴四边形EFBM为平行四边形.
作EN ⊥ AB于N,
EP= EF
1
2
(2)当P点在何处时,菱形AEPM的面积为四边形EFBM面积的一半?
例4.如图,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB、BC、CD、DA的中点分别为P、Q、M、N,试判断四边形PQMN为
怎样的四边形.并证明你的结论.
证明:连结AC,BD.
∵ PQ为△ABC的中位线,
∴ 四边形PQMN为平行四边形.
在△AEC和△DEB中,AE=DE,EC=EB,
∠AEC=∠DEB= 180°- 60° = 120° ,
∴ △AEC≌△DEB.
∴ AC=DB. ∴ PQ=PN. ∴ □PQMN为菱形.
∴PQ AC
∥
=
2
1
同理 ∴MN PQ
MN AC
∥
=
2
1
∥
=
1.判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等 的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一组对角的四边形是菱形.
√
╳
╳
╳
2.菱形两条对角线长为6和8,菱形的边长为 ,
面积为 。
5
24
3.菱形的面积为96,对角线AC长为16 ,此菱形的边长为 。
10
随堂练习
4.菱形对角线的平方和等于一边平方的 ( )
A. 2倍 B. 3倍 C.4倍 D. 5倍
C
5.把两张等宽的纸条如图交叉重叠在一起,
则重叠部分ABCD的形状是( )
A.平行四边形 B.矩形
C.菱形 D.任意四边形
A
C
D
B
C
(1)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O 作MN⊥BD,分别交AD,BC于点M,N .求证:四边形BNDM是菱形.
6、解答题
提示:证明 △ODM≌△OBN.NB=MD.
又 MD∥BN,MN⊥BD,结论得证。
(2)如图,AD∥BC,BD垂直平分AC,四边形ABCD一定是菱形吗?若是,请说明理由。
C
D
B
A
O
┐
) 1
2 (
提示:△AOD≌△COB AD=BC
(3)已知:□ABCD 的对角线AC的垂直平分线与边AD 、BC分别交于E、F
求证:四边形AFCE是菱形。
分析: (1)利用定义判定
(2) 由已知可知
OA=OC,EF⊥AC.
(3)利用四边相等,你会吗?
(4)如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,证明:CE⊥DF.
A
B
F
N
D
M
E
C
提示:证明四边形DMNC是菱形
(5)已知:如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD、PC相交于点P。 (1)猜想:四边形PCOD是什么特殊的四边形?证明你的猜想。
(2)PO与CD有怎样的关系?
四边形PCOD是菱形。
PO⊥CD,且互相平分。
(6)如图,CD为Rt△ABC斜边AB上的高,∠BAC的平分线交CD于E,交BC于F,FG⊥AB于G.
求证:四边形EGFC为菱形.
G
F
E
D
C
B
A
(7)如图,Rt△ABC中,∠ACB=900,∠BAC=600,DE垂直平分BC,垂足为D,交AB于E,又点F在DE的延长线上,且AF=CE,求证:四边形ACEF是菱形。
F
E
D
C
B
A
易得:CE∥FG,再证△ACE≌ △AGE
∠B=∠ACD=∠AGE ,EG∥CF,
四边形EGFC是平行四边形,又CE=EG,
四边形EGFC为菱形.
AC=AF=EF=CE
菱形常用的判定方法:
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有四条边相等的四边形是菱形.
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
平行四边形
菱形
对角线互相垂直且平分
作业:P70 A 3、4、5 B 8
知识总结
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
